Сурнева О.Б.
ФГАОУ ВПО «Северо-Кавказский федеральный университет»,
Россия
3-мерная модель и ее решения
Предметом исследования является наличие свойства
Пенлеве у дифференциального уравнения с частными производными
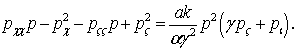 (1)
(1)
где ![]() - постоянные,
- постоянные, ![]() - функция трех
независимых переменных.
- функция трех
независимых переменных.
Согласно [1], уравнение с частными
производными имеет свойство Пенлеве, если все подвижные особые области его
общего решения, если они существуют, полярны. Подвижные особые области – это
такие особые области, положение которых зависит от произвольных функций
интегрирования и которые не являются характеристическими. Если дифференциальное
уравнение с частными производными n-го порядка для функции ![]() имеет свойство Пенлеве,
то его решение, представленное в виде ряда
имеет свойство Пенлеве,
то его решение, представленное в виде ряда
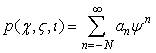 (2)
(2)
где ![]() , содержит две произвольные независимые между собой
функций от
, содержит две произвольные независимые между собой
функций от ![]() (их число обусловлено
порядком уравнения), среди которых
(их число обусловлено
порядком уравнения), среди которых ![]() и один из резонансных
коэффициентов
и один из резонансных
коэффициентов ![]() (
(![]() - резонансные числа) [2,3].
- резонансные числа) [2,3].
ЛЕММА
1. Для наличия у дифференциального
уравнения с частными производными (15.1) свойства Пенлеве необходимо, чтобы
соответствующее ему обыкновенное уравнение
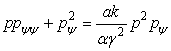 (3)
(3)
имело
свойство Пенлеве.
ДОКАЗАТЕЛЬСТВО.
Определим поведение главной части решения уравнения в окрестности подвижной
особенности. Для этого представим функцию ![]() уравнения (1) в виде
уравнения (1) в виде ![]() .
.
Найдем,
для какого значения N ряд (2) может
удовлетворять уравнению (3), оценим степени главной части ряда Лорана, тогда подставив
в исходное уравнение (3) полученные оценки имеем
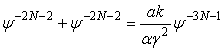 ,
,
следовательно,
старшие степени будут совпадать, если ![]() , откуда N = 1. Если бы N не являлось целым, то мы получили бы алгебраическую точку
ветвления и уравнение (1) не обладало бы свойством Пенлеве. И так, решение
будет иметь полюс первого порядка.
, откуда N = 1. Если бы N не являлось целым, то мы получили бы алгебраическую точку
ветвления и уравнение (1) не обладало бы свойством Пенлеве. И так, решение
будет иметь полюс первого порядка.
Определим,
какую структуру будет иметь ![]() , для этого сравним какие члены в уравнении (1) дают старшие
степени при подстановке значения
, для этого сравним какие члены в уравнении (1) дают старшие
степени при подстановке значения ![]() , оказывается, что все члены дают -4 степень, но среди них
есть три слагаемых
, оказывается, что все члены дают -4 степень, но среди них
есть три слагаемых ![]() , которые содержат производные по переменной
, которые содержат производные по переменной ![]() , поэтому вид зависимости от
, поэтому вид зависимости от ![]() положим линейным и
положим линейным и ![]() , пусть
, пусть ![]() где
где ![]() - произвольная
функция.
- произвольная
функция.
Для
нахождения резонансных чисел ![]() , выполнив подстановку
, выполнив подстановку ![]() в уравнение (1) получим
следующие коэффициенты в левой и правой части при
в уравнение (1) получим
следующие коэффициенты в левой и правой части при ![]() , которые дают следующее резонансное условие:
, которые дают следующее резонансное условие:
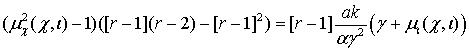 . (4)
. (4)
Очевидно,
что при ![]() будем иметь в
равенстве (4) тождественный нуль. Числу
будем иметь в
равенстве (4) тождественный нуль. Числу ![]() отвечает
произвольность функции
отвечает
произвольность функции ![]() и
и ![]() изначально выбирается
произвольной. Все остальные коэффициенты ряда выражаются рекуррентно.
изначально выбирается
произвольной. Все остальные коэффициенты ряда выражаются рекуррентно.
Решение уравнения в виде
формального ряда Лорана
Выделив
главную часть в разложении (2)
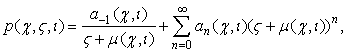 (5)
(5)
подставим (5) в (1),
решаем полученное уравнение относительно ![]() . Соберем члены с одинаковыми степенями, получим равенство,
которое распадается по степеням
. Соберем члены с одинаковыми степенями, получим равенство,
которое распадается по степеням ![]() :
:
![]()
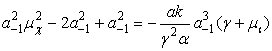 , (6)
, (6)
это равенство может иметь два решения:
А(-4). Если
старший коэффициент ![]() является функцией,
тогда
является функцией,
тогда
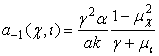 . (7)
. (7)
Б(-4). Как
это бывает обычно при исследовании на свойство Пенлеве, старший коэффициент ![]() полагают равным
постоянной величине, в нашем случае это возможно при дополнительных условиях,
задаваемых на функцию
полагают равным
постоянной величине, в нашем случае это возможно при дополнительных условиях,
задаваемых на функцию ![]() . Положим для компенсации коэффициентов в равенстве (6)
. Положим для компенсации коэффициентов в равенстве (6) ![]() .
.
ЛЕММА 2(Б). Чтобы функция ![]() и резонансный
коэффициент
и резонансный
коэффициент ![]() ряда (5), представляющего решение уравнения
(1), был произвольной независимой функцией от
ряда (5), представляющего решение уравнения
(1), был произвольной независимой функцией от ![]() , необходимо выполнение следующего условия:
, необходимо выполнение следующего условия:
![]() . (8)
. (8)
Найдем явный вид
нескольких последующих коэффициентов разложения.
![]()
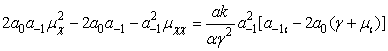 ; (9)
; (9)
А(-3). При подстановке значения ![]() (7) в левую часть (9)
остается
(7) в левую часть (9)
остается
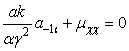 . (10)
. (10)
ЛЕММА 2(А). Чтобы функция
![]() и резонансный
коэффициент
и резонансный
коэффициент ![]() ряда (5), представляющего решение уравнения
(1), был произвольной независимой функцией от
ряда (5), представляющего решение уравнения
(1), был произвольной независимой функцией от ![]() , необходимо выполнение следующего условия:
, необходимо выполнение следующего условия:
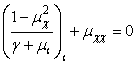 ,
(11)
,
(11)
Б(-3). При выполнении леммы 2(Б) в равенстве (9) остается единственный член ![]() , что приводит к необходимости положить дополнительно
, что приводит к необходимости положить дополнительно ![]() , а это означает, что
, а это означает, что ![]() - линейно зависит от
- линейно зависит от ![]() , т.е.
, т.е. ![]() , тогда в силу (8) приходим к соотношению на функции
, тогда в силу (8) приходим к соотношению на функции ![]() :
:
![]() ,
,
равенство возможно при
условии ![]() , тогда
, тогда ![]() , (постоянную интегрирования положили равной нулю) в
результате получилась
, (постоянную интегрирования положили равной нулю) в
результате получилась
![]() , (12)
, (12)
где ![]() - произвольная
постоянная, и
- произвольная
постоянная, и ![]() и
и ![]() одновременно не равны
нулю, при этом
одновременно не равны
нулю, при этом ![]() - остается
произвольной функцией.
- остается
произвольной функцией.
![]()
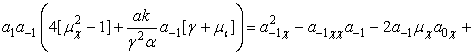
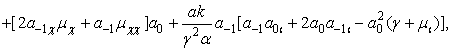 (13)
(13)
из полученного равенства находим ранее
неизвестный коэффициент ![]() :
:
А(-2). С
учетом равенства (10), получаем следующее значение
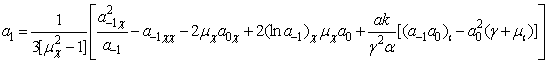 . (14)
. (14)
Б(-2).
Используя (12), находим
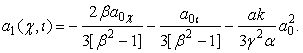 (15)
(15)
Для произвольной
степени ![]() запишем общее уравнение и найдем рекуррентную
формулу для определения последующих коэффициентов
запишем общее уравнение и найдем рекуррентную
формулу для определения последующих коэффициентов ![]() ряда Лорана
ряда Лорана
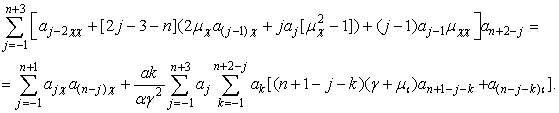 (16)
(16)
Выделим члены, содержащие старшие
коэффициенты ![]() , каждый коэффициент определяется единственным образом через
ранее определенные
, каждый коэффициент определяется единственным образом через
ранее определенные
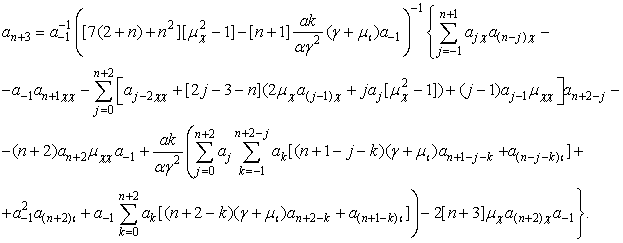
Для случая А(n):
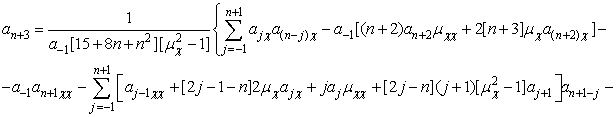
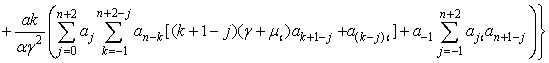 (17)
(17)
Произведенные исследования позволяет сформулировать
следующую теорему.
ТЕОРЕМА
1(А). Нелинейное уравнение (1) в случае выполнения
для функции ![]() дополнительного условия (11) обладает свойством Пенлеве.
дополнительного условия (11) обладает свойством Пенлеве.
ТЕОРЕМА 2(А). Нелинейное
уравнение (1) имеет решение в виде формального ряда (5) с коэффициентами,
определяемыми по рекуррентной формуле (17), где старший коэффициент ![]() определяется в
виде (12),
определяется в
виде (12), ![]() - произвольная
функция, функция
- произвольная
функция, функция ![]() удовлетворяет нелинейному уравнению в частных
производных (11).
удовлетворяет нелинейному уравнению в частных
производных (11).
Для
случая Б(n):
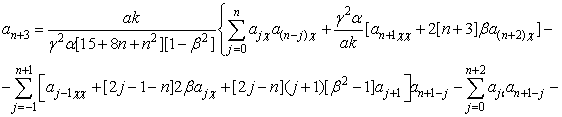
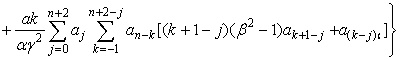 (18)
(18)
Обобщим полученный результат в виде теоремы.
ТЕОРЕМА 3(Б). Нелинейное
уравнение (1) имеет решение в виде ряда
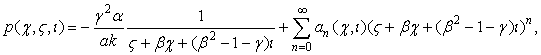
с коэффициентами, определяемыми по
рекуррентной формуле (18), где старший коэффициент ![]() ,
, ![]() - произвольная
функция,
- произвольная
функция, ![]() - произвольный
параметр.
- произвольный
параметр.
Частные решения в виде
ряда Лорана
Полученное решение в теореме 1 имеет
дополнительное условие, накладываемое на функцию - (11). Рассмотрим два частных случая, когда ![]() зависит только от
одной переменной.
зависит только от
одной переменной.
I. Пусть ![]() - функция одной
переменной, тогда
- функция одной
переменной, тогда ![]() и коэффициенты примут
вид:
и коэффициенты примут
вид:
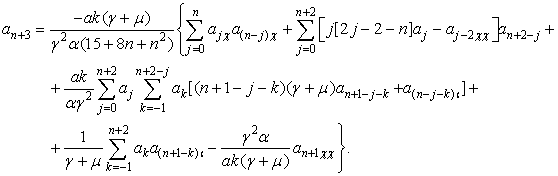 (19)
(19)
ТЕОРЕМА 4. Нелинейное
уравнение (1) имеет решение в виде ряда
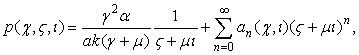
с коэффициентами, определяемыми по
рекуррентной формуле (19), где старший коэффициент 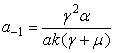 ,
, ![]() - произвольная
функция,
- произвольная
функция, ![]() - произвольный
параметр.
- произвольный
параметр.
II. Частное решение (11) в виде
бегущей волны ![]() .
.
ТЕОРЕМА 5. Уравнение (1)
имеет решение в виде формального ряда
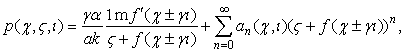
с коэффициентами, определяемыми по
рекуррентной формуле (17), где ![]() ,
, ![]() ,
, ![]() - произвольные дифференцируемые функции.
- произвольные дифференцируемые функции.
II. Пусть ![]() , тогда условие (11) примет решение
, тогда условие (11) примет решение
![]() . (20)
. (20)
ТЕОРЕМА 6. Нелинейное
уравнение (1) имеет решение в виде
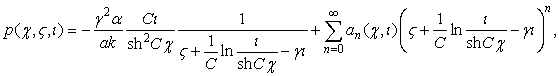
с коэффициентами, определяемыми по
рекуррентной формуле (17), ![]() - имеет вид (20),
- имеет вид (20), ![]() - произвольная
функция,
- произвольная
функция, ![]() - произвольный
параметр.
- произвольный
параметр.
Литература
1. Cosgrove C.M.
Painleve classification of all similinear partial differential equations of the
second order. – Stud. Appl. Math. 1993. V. 89. P. 1-61.
2. Кудряшов Н.А. Аналитическая теория
нелинейных дифференциальных уравнений. – М: Ижевск. АНО «Институт компьютерных исследований», 2004, с. 359.
3. Weiss
J., Tabor M., Carnevale G. The Painleve property for partial differential
equations. – J. Math. Phys. 1983. V. 24. № 3. P. 522 – 526.
4. Сурнева О.Б. 2+1 –мерное дифференциальное уравнение в частных производных обладающее парой Лакса//Materiály VIII mezinárodní vědecko -
praktická konference «Zprávy vědecké ideje - 2012». - Díl 21. Matematika.
Fyzika. Moderní informační technologie. Výstavba a architektura:
Praha. 2012. С. 3-5.