К. физ.-мат. н. Редькина Т.В.

ФГАОУ ВПО «Северо-Кавказский федеральный университет», Россия

Дифференциальные связи между нелинейными системами

В литературе, связанной с преобразованиями одного уравнения в другое особое место занимают дифференциальные связи [1]. Соотношение

(или набор таких соотношений) отображает в , если любое (локальное) решение уравнения однозначно определяет некоторое (локальное) решение уравнения .

Примерами таких отношений могут служить преобразования Коши – Римана, Миуры, Коула и Хопфа [2, 3] и др. объединенные под более общим понятием – преобразования Бэклунда [4].

Набор соотношений, включающих , и производные и , является преобразованием Бэклунда между и , если:

1) преобразование Бэклунда является интегрируемым для , если и только если ;

2) преобразование Бэклунда является интегрируемым для , если и только если ;

3) по заданному , такому, что , преобразование Бэклунда позволяет определить с точностью до конечного числа констант, причем ;

4) по заданному , такому, что , преобразование Бэклунда позволяет определить с точностью до конечного числа констант, причем .

Клэрэном разработан метод построения преобразований Бэклунда более общего вида для уравнений второго порядка типа Монжа – Ампера

.

В статье развиты идеи Клэрэна и построены дифференциальные связи, преобразующие заданную систему двух уравнений на функции :

(1)

в некую, пока неизвестную систему двух уравнений на функции того же порядка.

Так как исходная система описывает связь двух функций от двух переменных , то для задания перехода от одной системе к другой необходимо задать две пары, характеризующие дифференциальные преобразования по независимым переменным х и t. Исходя из того, что рассматриваемая система (1) по переменной х третьего порядка, а по переменной t – первого, и для построения (1) используется перекрестное дифференцирование, следует задать дифференциальные соотношения по переменной t – первого порядка, а по переменной х – второго порядка:

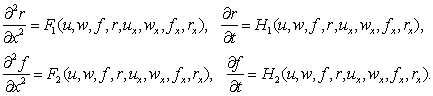
ТЕОРЕМА 1. Нелинейные системы в частных производных (1) и

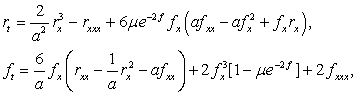(2)

связаны между собой преобразованиями Бэклунда вида:

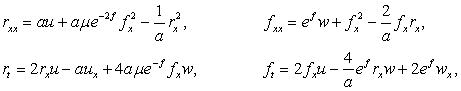(3)

где - дифференцируемые функции двух независимых переменных, , - произвольные параметры отличные от нуля.

ТЕОРЕМА 2. Нелинейные системы уравнений (1) и

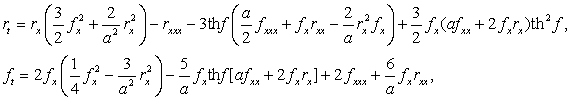
связаны между собой преобразованиями Бэклунда вида:

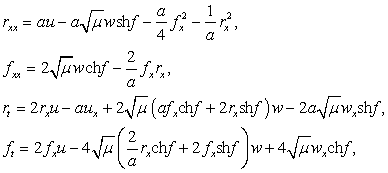
где - дифференцируемые функции двух независимых переменных, , - произвольные параметры отличные от нуля.

Рассмотрим преобразования Бэклунда (3), полученные в теореме 1 и выполним замену функций на :

. (4)

Для выполнения полной замены на новые функции вторую пару равенств (3) необходимо предварительно продифференцировать по переменной х, тогда

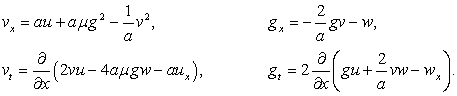(5)

Первая строка дает явный вид представления функций через две другие функции:

. (6)

Если предположить, что , то полученная связь имеет члены подобные известному преобразованию Миуры () [2, 3], которое определяет соответствие между уравнением КдВ и модифицированным уравнением КдВ, поэтому можно считать, что (6) является некоторым аналогом этого преобразования.

Выполним подстановку (6) в равенства второй строки (5), в результате получим систему двух уравнений

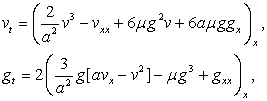(7)

каждое является возмущением модифицированного уравнения КдВ.

ТЕОРЕМА. Системы уравнений в частных производных (1) и (7) связаны преобразованиями (6).

Доказательство. Выполним подстановку (6) в (1). Преобразуем первое уравнение и выделим полные производные

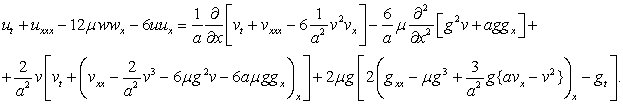
В полученном равенстве можно вынести линейный оператор :

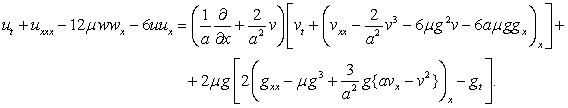(8)

Проведем такие же действия со вторым равенством системы (1) и вынесем оператор за скобки, тогда получим

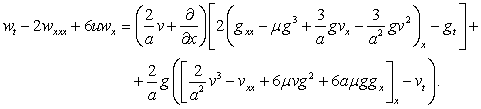(9)

Если функции являются решением системы (1) и , то при условии из (8) и (9) следует, что функции - решение системы (9).

СЛЕДСТВИЕ. Комплексификация уравнения Кортевега – де Вриза (КдВ)[5]

и 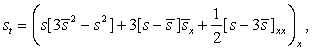(10)

связаны преобразованием

где - комплексные функции независимых переменных .

Схема доказательства полностью совпадает с доказательством теоремы приведенной выше, где полагаем

а параметры .

Если в равенстве (10) положить, что - действительная функция, то получим обычное модифицированное уравнение КдВ

поэтому (10) можно считать модификацией комплексификации уравнения КдВ.

Литература

1. Лэм Д.Л. Введение в теорию солитонов. – М.: Мир, 1983. – 294 с.

2. Miura R. M. Conservation laws for the fully nonlinear long-wave equations / R. M. Miura // Stud. Appl. Math. – 1974. – V. 53. – P. 45 – 56.

3. Miura R.М. Korteweg-de Vries equation and generalizations II. Existence of conservation laws and constants of motion / R.М. Miura, С.S Gardner, M.D. Kruskal // Journal of Mathematical Physics. – V. 9. – 1968. – P. 1204 – 1209.

4. Рыбников А. К. Связности Бэклунда и отображения Бэклунда, соответствующие эволюционным уравнениям второго порядка / А.К. Рыбников, К.В. Семенов // Известия высших учебных заведений. Математика. – 2004. – № 5. – С. 52 – 68.

5. Редькина Т.В. Комплексификация иерархии уравнения Кортевега – де Вриза. СКФУ Ставрополь: 2015. С. 130.