К.ф.- м.н., доц. А. В.
Макаричев, А. А. Кудь, А. Б. Щукин
Харьковский национальный автомобильно-дорожный
университет
Национальный аэрокосмический университет «ХАИ»
Московский государственный университет им. М.В.
Ломоносова
АЛЬТЕРНИРУЮЩИЕ
ПРОЦЕССЫ РАЗМНОЖЕНИЯ
На площадку поступают два вида частиц ![]() и
и ![]() . Если на площадке одновременно находятся две частицы разных
видов, то они немедленно взаимно поглощаются и исчезают с площадки. Таким
образом, на площадке либо вообще нет частиц, либо там есть частицы только одного
вида из двух
. Если на площадке одновременно находятся две частицы разных
видов, то они немедленно взаимно поглощаются и исчезают с площадки. Таким
образом, на площадке либо вообще нет частиц, либо там есть частицы только одного
вида из двух ![]() или
или ![]() . Обозначим через
. Обозначим через ![]() состояние, когда на
площадке нет ни тех, ни других частиц. Пусть
состояние, когда на
площадке нет ни тех, ни других частиц. Пусть ![]() - состояние, когда на
площадке
- состояние, когда на
площадке ![]() частиц вида
частиц вида ![]() и
и ![]() - состояние, когда на
площадке
- состояние, когда на
площадке ![]() частиц вида
частиц вида ![]() . Пусть в некоторый момент времени процесс находится в
состоянии
. Пусть в некоторый момент времени процесс находится в
состоянии ![]() (
(![]() ). Тогда предполагается, что спустя случайное распределенное
по показательному закону распределения с параметром
). Тогда предполагается, что спустя случайное распределенное
по показательному закону распределения с параметром ![]() время он либо с вероятностью
время он либо с вероятностью
![]() переходит в состояние
переходит в состояние
![]() (число положительных
частиц увеличивается на единицу), либо с вероятностью
(число положительных
частиц увеличивается на единицу), либо с вероятностью ![]() он переходит в
состояние
он переходит в
состояние ![]() (число положительных
частиц уменьшается на единицу). Из состояния
(число положительных
частиц уменьшается на единицу). Из состояния ![]() спустя случайное
распределенное по показательному закону с параметром
спустя случайное
распределенное по показательному закону с параметром ![]() время процесс либо с
вероятностью
время процесс либо с
вероятностью ![]() переходит в состояние
переходит в состояние
![]() (число положительных
частиц становится равным единице), либо с вероятностью
(число положительных
частиц становится равным единице), либо с вероятностью ![]() он переходит в
состояние
он переходит в
состояние ![]() (число отрицательных
частиц становится равным единице). Если
же в некоторый момент времени процесс находится в состоянии
(число отрицательных
частиц становится равным единице). Если
же в некоторый момент времени процесс находится в состоянии ![]() (
(![]() ). Тогда предполагается, что спустя случайное распределенное
по показательному закону распределения с параметром
). Тогда предполагается, что спустя случайное распределенное
по показательному закону распределения с параметром ![]() время он либо с
вероятностью
время он либо с
вероятностью ![]() переходит в состояние
переходит в состояние
![]() (число отрицательных
частиц уменьшается на единицу), либо с вероятностью
(число отрицательных
частиц уменьшается на единицу), либо с вероятностью ![]() он переходит в
состояние
он переходит в
состояние ![]() (число отрицательных
частиц увеличивается на единицу). Для вероятностей состояний
(число отрицательных
частиц увеличивается на единицу). Для вероятностей состояний ![]() (
(![]() - целые неотрицательные числа и
- целые неотрицательные числа и ![]() ) в момент времени
) в момент времени ![]() справедлива счетная
система дифференциальных уравнений Колмогорова [1]
справедлива счетная
система дифференциальных уравнений Колмогорова [1]
…………………………………………………………….
![]() ,
, ![]()
…………………………………………………………….
![]()
……………………………………………………………
![]() ,
, ![]()
…………………………………………………………...
При выполнении необходимых и достаточных условий [3]
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
существуют стационарные вероятности состояний
альтернирующего процесса размножения, то есть пределы
![]() ,
, ![]() (
(![]() - целые неотрицательные числа и
- целые неотрицательные числа и ![]() ).
).
Для этих стационарных вероятностей справедлива счетная
система линейных уравнений
……………………………………………………………………..
![]() ,
, ![]()
……………………………………………………………………..
![]()
……………………………………………………………………..
![]() ,
, ![]() ,
,
из которой эти вероятности можно определить как
![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где
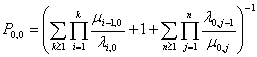 .
.
Пример 1. Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда 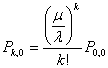 ,
, 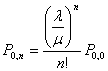 , где
, где
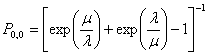 .
.
Пример 2. Пусть ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда при
. Тогда при ![]()
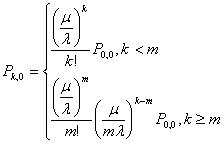 ,
, 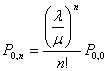 , где
, где
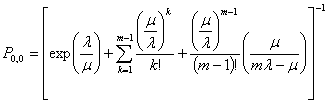 .
.
Литература.
1. B. V. GNEDENKO AND
I. N. KOVALENKO, Introduction to Queueing
Theory, Program for Scientific Translations, Jerusalem, 1968.
2. Соловьев А. Д. Асимптотическое поведение
момента
наступления редкого события в регенерирующем процессе.
Известия АН СССР. Техническая кибернетика, 1971, № 6, с.
79-89.
3. Вопросы математической теории надежности
/Е.Ю.
Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,
А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:
Радио и связь, 1983.- 376 с., ил.
4. Ширяев А.Н. Вероятность, М.: Наука,
1980, 576 c.