УДК 532:536.24; 539.3.

Божанов Е.Т., Ибраимкулов А.М.,Касымюекова М.,Абыдгалиева А.К.

Казахский Национальный Технический Университет имени К.И. Сатпаева

Расчет тонкостенной длинной конструкции под действием ударного импульса , лежащей на основании типа Коссера , когда сила контактного воздействия сосредоточенная скользящая и свободная под нагрузкой

Анатация. В данной статье рассмотрена длинная тонкостенная конструкция под воздействием ударного импульса , когда сила контактного воздействия сосредоточенная , скользящая и свободная под нагрузкой.

Постановка задачи.

В качестве мишени рассмотрим тонкостенную длинную конструкцию , толщиной – һ с переменными параметрами поперечного сечения, лежащую на обобщенном оснований типа Коссера[1] – [2] .

Пусть на поверхность конструкции действует критический импульс в виде неправомерной поперечной силы произвольной эпюры. При этом размеры площади контакта взаимодействующих тел и форма критической деформации зависят от эпюры неравномерной поперечной силы.

Ударный импульс производиться в центре плоскости мишени в начало координатной системы , в зоне контакта происходят относительные удлинения и смещения деформации.

Математическую модель взаимодействующих тел в зависимости дифференциального уравнения изгиба срединой оси поперечного сечения возьмем в виде [3] – [4]:

(1)

где D – жесткость сечения конструкции ,В – новая константа материала основании типа Коссера , имеющая размерность силы ,k – коэффициент основания типа Винклера , - активная критическая нагрузка перечного сечения.

Вводя безразмерную координату:

(2)

И подставляя значения в уравнении (1) получим :

(3)

Общее решение (3) представим в виде :

(4)

где - какое – нибудь частное решение дифференциального уравнения (3) , которое очень легко определиться в зависимости от вида правой части , – общее решение однородного уравнения :

(5)

Так как коэффициент 2В – намного меньше чем модуль Юнга , то коэффициент 0 ≤ с ≤ 1 . При этом с=0 получим модуль Б – 2 , конструкция лежащая на основании типа Винклера.

(6)

Характеристическое уравнение дифференциального уравнения (5) имеет вид:

Все корни характеристического уравнения комплексные , так как 0 ≤ с ≤ 1. Воспользовавшись симметрией , ограничивая рассмотрением только правой части тонкостенной конструкции из условия на бесконечности общее решение дифференциального уравнения (3) имеет вид :

Здесь - действительные и мнимые части корней (±і) , (±і) характеристического уравнения (7) , .

В качестве примера рассмотрим простые случаи расчета тонкостенной конструкции бесконечной длины , загруженную сосредоточенной силой , когда сила контактного воздействия скользящая и свободная под нагрузкой.

1.1 Расчет тонкостенной длинной конструкции под действием ударного импульса, лежащей на основании типа Коссера, когда сила контактного воздействия сосредоточенная под нагрузкой.

В данном случае ,граничные условия есть:

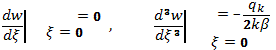(9)

А общее решение при :

Подставляя (10) в (9) определим произвольные интегрирования , а затем их значения подставляя (10) получим :

(11)

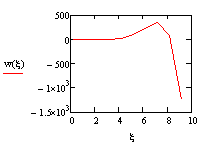
Уравнение (11) решено на ЭВМ при следующих данных:

С=0,17 :

ξ= {0,2;0,4;0,6;0,8;1,0;1,2;…10,0}

1.2 Расчет тонкостенной длинной конструкции под действием ударного импульса, лежащей на основании типа Коссера, когда сила контактного воздействия скользящая под нагрузкой.

В данном случае ,граничные условия есть:

(12)

А общее решение при :

Подставляя (13) в (12) определим произвольные интегрирования , а затем их значения подставляя в общее решение получим :

Уравнение (14) решено на ЭВМ при следующих данных:

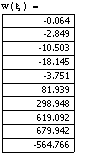С=0,18 :

ξ= {0,2;0,4;0,6;0,8;1,0;1,2;…10,0}

1.3 Расчет тонкостенной длинной конструкции под действием ударного импульса, лежащей на основании типа Коссера, когда сила контактного воздействия свободная под нагрузкой.

В данном случае ,граничные условия есть:

А общее решение при :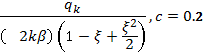

Подставляя (16) в (15) определим произвольные интегрирования , а затем их значения подставляя в общее решение (16) получим :

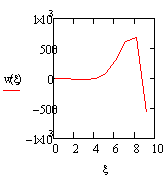
Уравнение (17) решено на ЭВМ при следующих данных:

С=0,2 :

ξ= {0,2;0,4;0,6;0,8;1,0;1,2;…10,0}

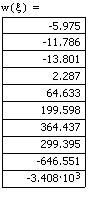
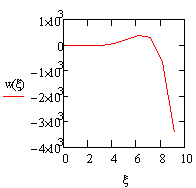
Вывод. На графиках 1 – 3 приведены линии возможных микротрещин материалов и какое возможное разрушение вызывает ударный импульс при относительном удлинении деформации площади контакта.

Предварительное нагружение поперечного сечения площади контакта (внутреннее критическое напряжение в долях - ) уменьшает коэффициент динамичности ,

Плотность материала поперечного сечения площади контакта как переменная величина уменьшается согласно нормальному закону распределения плотностей непрерывных случайных величин.

Механизм относительных удлинений может быть представлен в виде приведенного момента инерции наименьшего радиуса поперечного сечения контактной площади.

Дифференциальное уравнения движения среды поперечного сечения может быть представлен в виде:

, ,

где – комплексные амплитуды ударного импульса, - комплексная податливость , w(t) – комплексные переменная , – кривизна изогнутой оси поперечного сечения площади контакта.

Литература

1. С.Н.Соколов , круглая пластинка на обобщенном упругом основании, Инжинерный сборник , т.2, 1952.

2. А.Р.Кер, Упругие и вязкоупругие модели основании , прикладная механика, 1964.

3. Е.Т.Божанов ,Ж.С.Ержанов , Исследование проблем устойчивости упругих тел, гибких пластин и оболочек и их приложения , «Қазақстан жоғары мектебі », Алматы, 2001, 300 с.

4. Партон В.З., Механика разрушения от теории к практике.М, Наука,1990, 239с.

5. Божанов Е.Т., Отарбаев Ж.О., БугановаС.К.,”Математическое моделирование геомеханических процессов ” Алматы, 2015, 145 с.