Евсеев В.И.,канд. физ-мат наук, доцент, Казань
О равномерной трехзначной логике
1.1.
Основные понятия
Равномерная
трехзначная логика, которую мы будем обозначать ![]() , характеризуется
универсумом
, характеризуется
универсумом ![]() , состоящим
из трех классов высказываний
, состоящим
из трех классов высказываний
![]() – ложные высказывания,
– ложные высказывания,
![]() – гипотетические
высказывания,
– гипотетические
высказывания,
![]() – истинные высказывания.
– истинные высказывания.
Каждому
указанному классу истинности соответствует значение функции истинности, которую
мы будем обозначать ![]() , при этом для равномерной трехзначной логики
эти значения каждого высказывания
, при этом для равномерной трехзначной логики
эти значения каждого высказывания ![]() определяются
из основной таблицы:
определяются
из основной таблицы:
|
|
|
|
|
|
|
0 |
|
1 |
Значения
функции истинности мы будем часто обозначать просто ![]() , если это не вызывает недоразумений по содержанию.
, если это не вызывает недоразумений по содержанию.
Из основной
таблицы следует, что функция истинности
удовлетворяет характеристическому основному уравнению:
![]() (1.1)
(1.1)
Для построения
отделяющих функций применяется следующая схема.
Из основного уравнения
для класса ![]() определяется
частичное произведение
определяется
частичное произведение
![]() .
.
Эта функция принимает
значение 0 на классах ![]() и
и
![]() ,а
для класса
,а
для класса ![]() получаем
получаем
![]() .
.
Поэтому отделяющая функция класса ![]() имеет
вид
имеет
вид
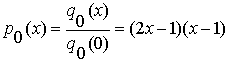 .
(1.2)
.
(1.2)
Для класса гипотез ![]() получаем
частичное произведение
получаем
частичное произведение
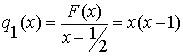 ,
,
значения которого для
классов ![]() и
и ![]() равны
нулю, а для класса
равны
нулю, а для класса ![]() получаем:
получаем:
![]() .
.
Значит, для класса ![]() получаем
получаем
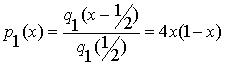 . (1.3)
. (1.3)
Для класса истинных
высказываний ![]() получаем
частичное произведение
получаем
частичное произведение
![]() ,
,
что приводит к значению
на этом классе:
![]() ,
,
таким образом, получаем
отделяющую функцию этого класса:
![]() .
(1.4)
.
(1.4)
Нам
будет также удобно пользоваться другими
выражениями этих функций:
![]() ,
,
![]() ,
(1.5)
,
(1.5)
![]() .
.
1.
2. Свойства отделяющих
функций
Прежде
всего, отметим, что само высказывание ![]() имеет
следующее символическое строение
имеет
следующее символическое строение
![]() . (2.1)
. (2.1)
Поэтому
можно найти его функцию истинности в виде
![]() .
.
Следовательно, с учетом
реальных значений, получим:
![]() . (2.2)
. (2.2)
Сумма трех отделяющих
функций равна единице:
![]() (2.3)
(2.3)
Эти функции условно ортогональны
с учетом основного уравнения.
Действительно, получаем:
![]()
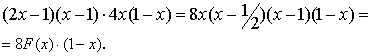 (2.4)
(2.4)
Аналогично, для двух
других произведений:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
Кроме того, они обладают
свойством условной идемпотентности в силу основного уравнения.
Так, для квадрата первой
отдаляющей функции получаем:
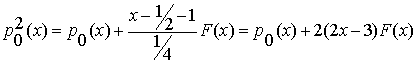 , (2.7)
, (2.7)
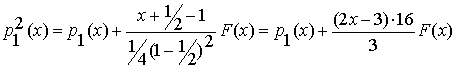 , (2.8)
, (2.8)
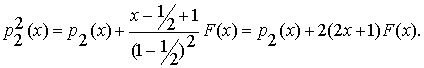 (2.9)
(2.9)
Таким образом,
отделяющие функции образуют полную ортогональную систему функций относительно
основного уравнения логики ![]() .
.
Нам будет удобно также
пользоваться связями между отделяющими функциями:
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
Эти
соотношения часто и эффективно применяются при изучении композиции различных
операций.
1.3.
Логические операции с
одной переменной
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Такие операции
называются унарными. Они в данном случае состоят из трех видов матричных
операций. Они описываются двумя системами циклических матриц третьего порядка.
Матрицы первого цикла состоят из единичной матрицы ![]() , которая имеет вид
, которая имеет вид
![]() =
=
А также двух
матриц, не имеющих неподвижных элементов (на главной диагонали):
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
![]() =
= ![]() =
=
Матрицы второго цикла имеют по одному
неподвижному элементу (на главной
диагонали)
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
![]() =
= ![]() =
= ![]() =
=
Эти матрицы обладают свойствами
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() =
=![]()
![]() =
=![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() =
=![]() ,
,
![]()
![]() =
=![]() ,
,
![]()
![]() =
=![]() , (3.1)
, (3.1)
![]()
![]() =
=![]() ,
,
![]()
![]() =
=![]() ,
,
![]()
![]() =
=![]() .
.
Теперь рассмотрим
последовательно сами эти операции.
а) Унарная операция
инверсии. Она определяется матрицей ![]() и характеризуется
симметрией относительно класса гипотез. Эта операция является аналогом операции
отрицания в классической логике.
и характеризуется
симметрией относительно класса гипотез. Эта операция является аналогом операции
отрицания в классической логике.
Инверсию можно задать в
матричной форме:
|
|
|
1 |
|
= |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
Значит, для инверсии
получаем:
![]() (X)=
(X)=![]() , (3.2)
, (3.2)
а функция истинности
имеет вид
![]() . (3.3)
. (3.3)
б)Аналогично,
для логического сдвига ![]() получаем
получаем
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
H |
|
|
|
E |
|
|
|
Е |
|
H |
Т (X) = =
Таким образом, для
преобразования высказывания находим:
![]() (X)=
(X)= ![]() , (3.4)
, (3.4)
а для
функции истинности получается формула:
![]() . (3.5)
. (3.5)
Подобная же
формула получается и для второго логического сдвига:
![]() ,
(3.6)
,
(3.6)
или в
матричном виде
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
Е |
|
Н |
|
|
|
H |
|
|
|
E |
![]() (X) =
=
(X) =
=
Это приводит
к формуле для функции истинности:
![]() .
(3.7)
.
(3.7)
Все
остальные унарные операции являются композициями изученных.
Литература:
1. Евсеев В.И. Основы
аналитической семантики. «Lambert».2014 г.
2. Евсеев В.И. Основные
понятия трехзначной «мягкой» логики.//Areas of
sciеntific thought.
Материалы XI международной научно-практической конференции , т.20(8 –
12). Sheffild. 2015 г.