Комолов В.М., к. физ.-мат. наук Латынин Ю.М.
Украинская инженерно-педагогическая
академия. г. Харьков
Розы как составляющие
трохоидальных кривых.
Введение. При изучении циклоидальных кривых в отдельную группу относят
так называемые трохоидальные розы, которые являются частным случаем трохоид [1,2].
Комплексная форма уравнений циклоидальных кривых, в [3] позволила предположить,
что розы являются составляющими
внутренней структуры трохоид. Обоснуем это положение, уточнив ряд
определений, следуя [1]. Эпициклоиды и гипоциклоиды − частные случаи циклоидальных
кривых, когда вычерчивающая их точка лежит на окружности производящего круга
радиуса r, при этом параметры m=r/R, s=d/R m=s характеризуют их свойства. Когда вычерчивающая
точка находится не на окружности
производящего круга, а отстоит от него на расстоянии d (s=d/R>1 или s=d/R < 1)
получают кривые, называемые трохоидами (s≠m). Последние подразделяют на
эпитрохоиды и гипотрохоиды, когда производящий круг катится по внешней или
внутренней стороне неподвижного круга
радиуса R. Если d < r (s< m) она будет укороченной, при d > r (s> m) − удлиненной, а при d=r (s= m) трохоида превращается в эпициклоиду или гипоциклоиду.
Розами или кривыми Гвидо Гранди называют семейство кривых, уравнение которых
в полярной системе координат имеет вид:
![]() (1)
(1)
где a, k − положительные постоянные. В соответствии с [1] к трохоидальным розам относят удлиненную
трохоиду, которая отвечает условию:
![]() (2)
(2)
и укороченную: ![]() . (21)
. (21)
Кривые (1) расположены внутри круга радиуса а и состоят из конгруэнтных лепестков (см.
ниже).
Основная часть. Теорема I. Уравнения трохоид в комплексной форме
описывают в общем случае два набора трохоидальных роз, каждый из которых включает
в себя розы, отвечающие уравнению
![]()
либо обобщенные
розы ![]() , где величины a, b, c, k считаются положительными.
, где величины a, b, c, k считаются положительными.
Уравнения эпитрохоид в комплексной форме представлены в [3]:
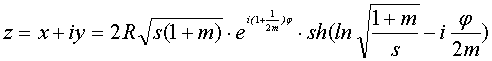 . (3)
. (3)
После ряда преобразований (3) получаем уравнение (31) [3]:
![]() , (4)
, (4)
где ![]() , а u* - сопряженный u комплекс.
, а u* - сопряженный u комплекс.
z= z1 +z2, где ![]() , причем:
, причем:
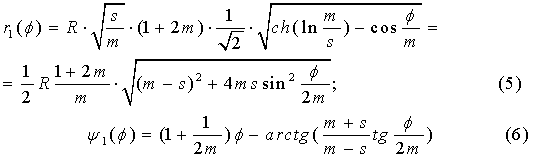
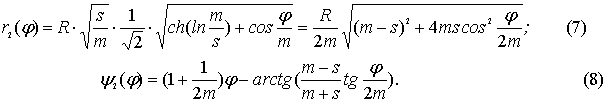
Из анализа (5÷8)
вытекает 2 вывода:
1.
Эпитрохоиды содержат два набора обобщенных трохоидальных роз: первый расположен
внутри круга радиуса ![]() , а второй из них − внутри окружности радиуса
, а второй из них − внутри окружности радиуса ![]() .
.
2. Результирующая кривая являет собой сумму двух наборов роз в полярной
системе координат (с учетом
аргументов Ψ1(φ); Ψ2(φ)).
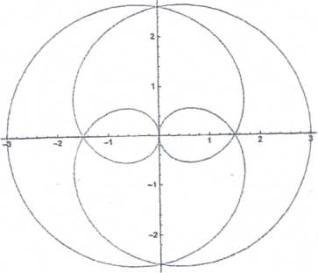
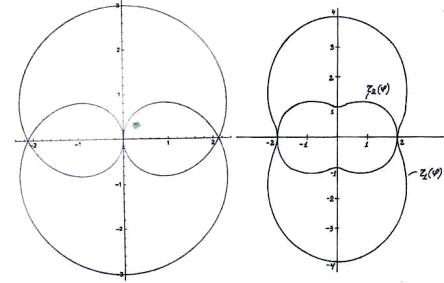
При m=1, s≠1 система уравнений (5÷8) соответствует
улитке Паскаля и для этой кривой справедливы п.1 и п.2 выводов. Система
уравнений упрощается в случае улитки Паскаля
– кардиоиды, которой соответствуют значения параметров m = 1 ; s=1. Она описывает две трохоидальные
розы:
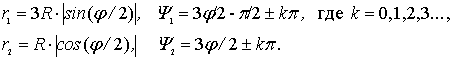 (9)
(9)
Графики кривых r1= r1(Ψ1) ; r2=r2(Ψ1) при R =1 приведены на рис. 1.
|
|
|
|
|
а) |
б) |
|
|
Рис.1. Зависимость r1(ψ1) (а), r2(ψ2) (б) при R=1 |
||
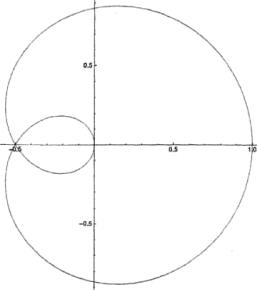
В [1] в качестве примера трохоидальной розы рассматривается
случай эпитрохоиды при m=1/2, s=1+m, график которой приведен на рис.2.
Покажем, что эту кривую можно представить как результат суперпозиции двух обобщенных
эпитрохоидальных роз. Уравнения (5-8) при указанных параметрах:
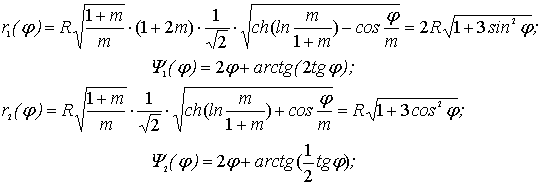
Графики r1= r1(φ); r2=r2(φ) при R=1 представлены на рис. 3.
Уравнения гипотрохоид в
комплексной форме из [3], (ф-ла 12):
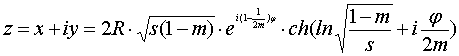 . (10)
. (10)
|
|
|
|
Рис.2. Трохоидальная роза: m=1/2, s=1+m |
Рис.3. Зависимость r1 (φ), r2( φ) |
В преобразованном виде:
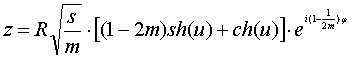 ; (11)
; (11)
![]() , где
, где
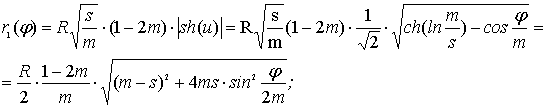 (12)
(12)
![]() ; (13)
; (13)
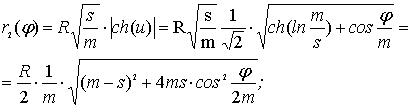 (14)
(14)
![]() . (15)
. (15)
Из анализа формул (12),
(14) вытекает, что и гипотрохоиды содержат два набора обобщенных трохоидальных
роз. Первый набор расположен внутри круга радиуса ![]() , а второй – внутри круга радиуса
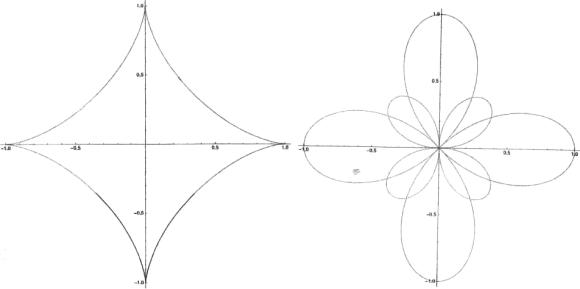
, а второй – внутри круга радиуса ![]() . Астроида − частный случай гипоциклоиды при m=s=1/4. Из (10) находим модуль
. Астроида − частный случай гипоциклоиды при m=s=1/4. Из (10) находим модуль ![]() и аргумент Ψ(φ)в этом случае:
и аргумент Ψ(φ)в этом случае:
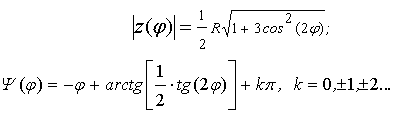 (16)
(16)
График астроиды при R=1 представлен на рис.4а. Из
(12÷15) составляющие астроиды имеют следующий вид:
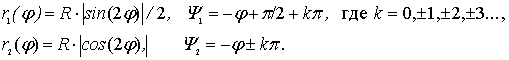 (17)
(17)
Каждая составляющая (17) есть четырехлепестковая роза, при этом
один набор сдвинут относительно второго на угол π/4 (рис. 4б).
Кривая Штейнера
(дельтоида) − также частный случай гипоциклоиды при m=s=1/3. Модуль ׀z(φ)׀;Ψ(φ) равны соответственно:
|
|
|
а) б) |
|
Рис. 4. Астроида (а) и зависимость r1(φ)
и r2 ( φ) -(б) |
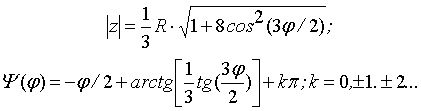 (18)
(18)
График кривой Штейнера
при R =1 представлен на рис. 5.
Составляющие уравнения, которые описывает эту кривую из (12-15):
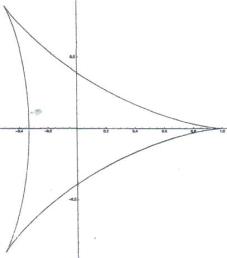
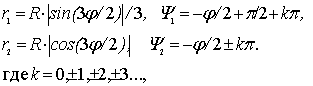 (19)
(19)
Каждая составляющая
(19) есть трехлепестковая роза, при
этом один набор сдвинут относительного второго на угол π/3.
Рис.5. Дельтоида
Выводы: Уравнения трохоид в комплексной
форме есть сумма двух слагаемых, каждому из которых соответствует семейство
трохоидальных роз (обыкновенных или обобщенных), и на ряде примеров
проиллюстрировано существование такой внутренней структуры трохоидальных кривых.
Список литературы:
1. Савелов А.А. Плоские кривые.
Систематика, свойства, применения. Справочн. руководство. - М.: Гос изд.
физ.-мат литературы, 1960.- 294 с.
2. Математическая энциклопедия:
гл. ред. И.М. Виноградов, М.: Советская энциклопедия, 1984, т.1-5.
3. Комолов В.М., Латынин Ю.М. Циклоидальные кривые: новая комплекс ная
форма уравнений. Materials of the X1 International Research and Practice сonference «Tendency modern science-2015», Vol.21, Mathematics,
Physics…. Sheffield. Science and
Education LTD.- P.26-34