Оленець С.Ю.

Міжнародний науково-навчальний центр інформаційних технологій та систем
НАН України та МОН України, м. Київ, Україна

Розв’язання задачі апроксимації QRS-комплексу ЕКГ у середовищі Excel

Вступ. В останні роки провідну роль у сучасній медицині відіграє комп’ютерний аналіз електрокардіограм. Він відкриває нові можливості в діагностиці патологій серця, що у свою чергу знижує ризик виявлення захворювання на пізніх стадіях. Це висуває нові завдання до комп’ютерного аналізу, що полягають у підвищенні точності вимірів, зменшенні об’єму збережених даних, швидкості їх передачі та захисті, з подальшим достовірним відтворенням вихідної інформації без втрати діагностично-важливих точок [1-3].

Серед усіх існуючих методів стиснення електрокардіограм, для досягнення поставлених завдань було обрано метод, який передбачає реконструкцію штучної ЕКГ реалістичної форми з використанням несиметричних Гаусових функцій. Він дозволяє кодувати ЕКГ- сигнал 25 параметрами. А при частоті дискретизації 500 Гц має ступінь стиснення 20:1 [4].

Мета. Метою даної роботи є відшукання рівняння кривої, яка б найкращим чином апроксимувала несиметричні зубці QRS- комплексу ЕКГ, задані на певному часовому проміжку.

Результати дослідження. Апроксимація даних сумою функцій Гауса використовується при інтерпретації різноманітних даних, у тому числі для дослідження стану серцевої активності пацієнта. При цьому визначається функціональна залежність рівня ЕКГ від часу для кожної складової комплексу, а їх апроксимація як кусково-задана функція. Ця функція є неперервною на заданому проміжку, так як границі справа і зліва кожного зубця ЕКГ у точці зміни коефіцієнтів масштабу сходяться в одній точці, що дає можливість використовувати систему рівнянь (1) для розв’язання поставленої задачі [5].

,

(1)

де – сумарна функція математичної моделі, , , , функції складових.

Для опису складової ЕКГ використовується функція (2), коефіцієнти масштабу якої будуть змінювати своє значення до і після точки екстремуму за формулою (3):

	(2)
	(3)

де – заданий час, – значення функції на заданому часовому проміжку, – коефіцієнт вершини зубця, – коефіцієнт зсуву зубця, а та – коефіцієнти масштабу лівого та правого плеча.

Нехай у результаті дослідження одержані табличні значення функції зубця QRS, що змінюється в часі .

			…
			…

((4)

Необхідно знайти систему із трьох рівнянь, кожне з яких набуває вигляду (2) та найкращим чином апроксимує табличні значення (4).

Розв’язувати дану задачу будемо за наступним алгоритмом:

1. Знаходимо екстремуми QRS-комплексу , , .

2. Визначаємо коефіцієнти зсуву зубців , , .

3. Знаходимо коефіцієнти та лівого та правого плеча кожного зубця комплексу.

Реалізацію даного алгоритму виконаємо у середовищі Excel. Значення екстремуму (максимуму або мінімуму) зубця знайдемо, використавши ітераційні методи. У Excel визначаємо його значення за допомогою вбудованого середовища програмування VBA.

Значення параметра (коефіцієнт зсуву відповідної компоненти) знаходиться у два кроки. На першому кроці визначаємо у якому рядку знаходиться значення екстремуму за допомогою середовища VBA. Потім знаходимо його величину за допомогою функції ИНДЕКС(A2:A60;Z73;1).

Для відшукання функції, яка найкращим чином описує початкові дані (4), скористаємося методом найменших квадратів: знайдемо таке значення , щоб . Для цього візьмемо логарифм від обох частин рівності (2). Одержимо функціонал:

(5)

Однак при подальшому пошуку параметрів, метод найменших квадратів виявляється неефективним, через виникнення проблеми близькості значень та (). Дану проблему можна вирішити шляхом переходу від функціоналу вигляду (5) до видозміненого функціоналу:

(6)

Знайшовши похідну функції і прирівнявши її до нуля, одержимо значення параметру _:

,

(7)

де відповідні суми обраховуються за формулами:

			(8)

Дані суми також обраховуємо за допомогою програмного середовища VBA.

Нехай зубець Q має коефіцієнти , , , , зубець R – , , , , зубець S – , , , , . Отримаємо наступні показники (з точністю до сотих): обрахований зубець Q , , R – , , S – , .

Одержаний графік показано на Рис. 1 (зеленим кольором позначені початкові дані, червоним – графік апроксимуючої функції).

Як бачимо з рисунку, знайдене рівняння кривої, навіть за наявності шуму, вдало описує задані табличні значення (4).

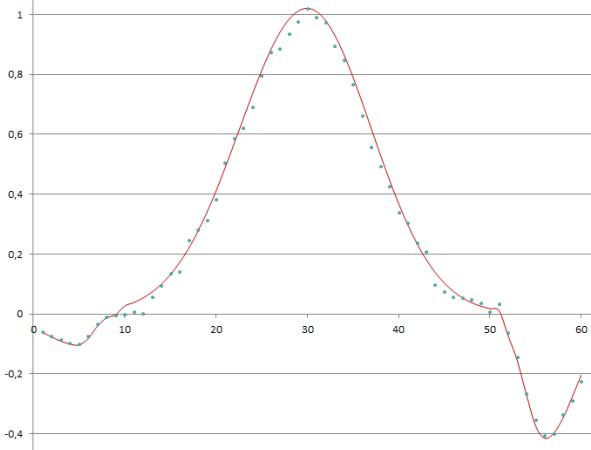
Рис. 1 Приклад апроксимації QRS- комплексу ЕКГ

Висновки. У даній роботі було реалізовано алгоритм знаходження коефіцієнтів рівняння, яке б найкращим чином апроксимувало табличні значення відповідного QRS- комплексу ЕКГ, заданого на певному часовому проміжку. У результаті дослідження одержано формули для знаходження коефіцієнтів зубців Q, R, S та перевірено їхню ефективність на практиці.

Подальшу роботу передбачається спрямувати на удосконалення методу знаходження параметрів масштабу «лівого» та «правого» плеча, а також на реалізацію алгоритму при знаходженні коефіцієнтів усіх зубців ЕКГ- комплексу.

Література:

1. Chaturvedi Ranjana A SURVEY ON COMPRESSION TECHNIQUES FOR ECG SIGNALS / Ranjana Chaturvedi, Mrs. Yojana Yadav // International Journal of Advanced Research in Computer and Communication Engineering. – 2013. – Vol. 2. – Issue 9. – P.3511-3513.

2. Karishma Qureshi Efficient data compression of ECG signal using Discrete Wavelet Transform / IJRET. – 2013. – Volume 2. – Issue 4. – P. 696-699.

3. Mayur Kumar Chhipa Performance Analysis of Various Transforms Based Methods for ECG Data / International Journal of Scientific and Research Publications. – 2013. – Volume 3. – Issue 5. – P. 1-6.

4. Файнзильберг Л.С. Технология построения телемедицинской системы на основе генеративной модели порождения искусственной ЭКГ реалистической формы. / Л.С. Файнзильберг // Клиническая информатика и Телемедицина. – 2012. – Т. 8. – Вып. 9. – С.89-98

5. Абрамов М.В. Аппроксимации экспонентами временного кардиологического ряда на основе ЭКГ. / М.В. Абрамов //Вестник кибернетики. — Тюмень: ИПОС СО РАН, 2010. — № 9. — С. 85–91.
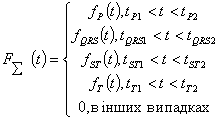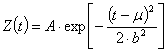
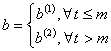
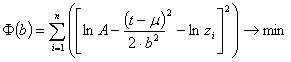
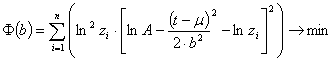
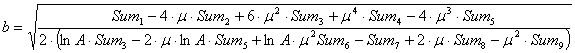