Бубнович Э.В.,
Абилденова Г.К.
Казахский национальный
технический университет имени К.И. Сатпаева,
г. Алматы, Республики
Казахстан
Автопараметрические колебания гибкой
пологой нити
1.Рассмотрим свободные колебания гибкой пологой
нити с неподвижными опорами на одном уровне. Будем считать, что нить
одновременно может совершать поперечные колебания относительно хорды,
соединяющей опорные закрепления. (рис. 1)
Поперечные перемещение нити будем
аппроксимировать выражением [1]
(1)
где
первое слагаемое в этой сумме – отклонение нити от действия статической
нагрузки 
второе слагаемое –
поперечное динамическое перемещение нити.
Выражение для кинетической энергии
имеет вид
(2)
где
- погонная
масса нити; 
- пролет; 
- угловое отклонение.
Потенциальная энергия системы
выражается в форме [6]
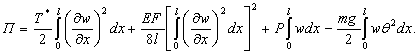(3)
Здесь
-
сила предварительного напряжения.
Подставляя (2) и (3) в уравнение
Лагранжа II рода и учитывая при этом (1), а также условие статического
равновесия нити [2], приходим к системе двух нелинейных дифференциальных
уравнений, которые в безразмерном виде запишутся следующим образом:
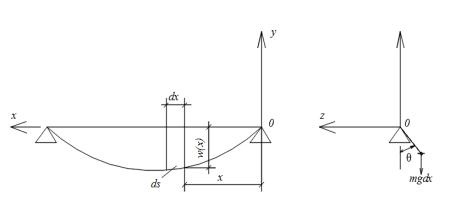
рис.1
Расчетная схема угловых колебании нити
(4) 
Где
и 
-
обобщенные координаты; 
; 
- отношение парциальных
частот линейных угловых и поперечных колебаний нити; Точками обозначено
дифференцирование по безразмерному времени τ. Коэффициенты 
определяются по следующем формулам
(4a)
2.Решение системы
уравнений (4) будем искать в виде асимптотических рядов по степеням малого
параметра
(5)
Здесь A, B, 
- вариационные параметры, описывающие
длиннопериодические колебательные изменения главных гармоник решения; 
… , 
, 
,
… - короткопериодические возмущения, представляющие, по существу, высшие
гармоники решения.
За
малый параметр принята безразмерная величина 
.
Подставляя
(5) в (4), получим
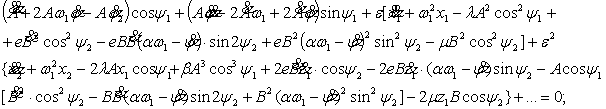(6) 
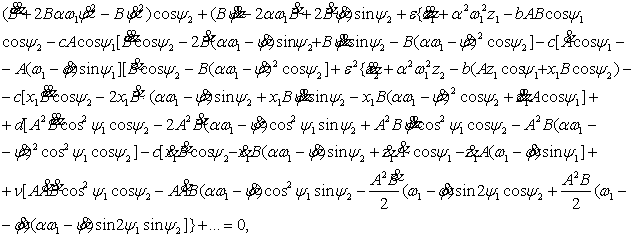
где 
3. Если считать, что вариационные
параметры в системе (6) постоянны, то сохраняя лишь члены первого порядка по 
, будем иметь
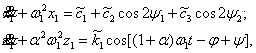(7)
где 
(7a)
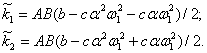
При 
уравнения (7) имеют
частные решения
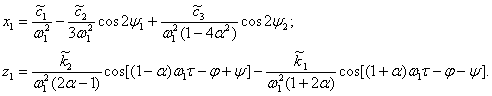(8)
Равенства
(8) представляют собой нерезонансное решение первого порядка.
4. Введем определение.
Максимальная степень резонирующих
членов в правых частях уравнений (4) называется рангом внутреннего резонанса.
Покажем, что резонанс второго ранга
(или главный внутренний резонанс) системы (4) возможен только при 
Предположим, что вариационные параметры
в системе (6) являются некоторыми функциями времени с производными порядка 
Тогда
с точностью до малых первого порядка получим
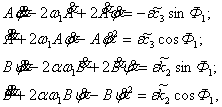(9)
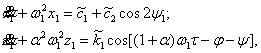(10)
где
кроме того, для
преобразования членов, становящихся резонансными при 
использованы
элементарные тождества
(10a)
Частные решения уравнений (10)
запишутся в форме
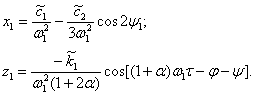(11)
Заменим
(9) приведенной вариационной системой. С точностью до величин первого порядка
относительно 
получим
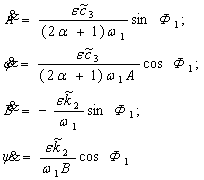(12)
Используя первое и третье уравнения
этой системы, найдем
(13)
С помощью (9), (12) и (13) получим
автономную систему уравнений относительно переменных 
и 
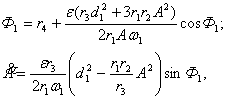(14)
где 
Систему (14) можно проинтегрировать,
поскольку, исключая из нее 
, получается дифференциальное соотношение
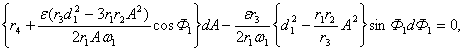(15)
которое
приводит к интегралу
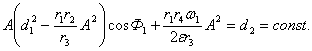(16)
Таким образом, из равенства (14)
получим следующее соотношение
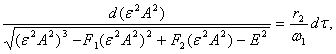(17)
где 
Выражение (17) показывает, что квадрат
амплитуды поперечных колебаний нити является эллиптической функцией времени.
Нетрудно видеть, что для 
близких к ½
корни знаменателя относительно 
в (17) будут иметь
действительные значения. Если их обозначить через 
где 
то решения, имеющие физический смысл, будут лежать в
интервале 
Из (17) будем иметь
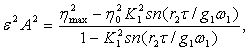(18)
где модуль
функции синус-амплитуды есть
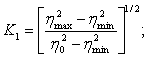
(19)
Период колебаний по 
выражается
эллиптическим интегралом I рода
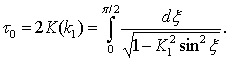(20)
В том случае, когда 
не
близко к 1/2, изменения А и 
становятся быстрыми,
поэтому соответствующие короткопериодические возмущения лучше описываются
нерезонансной формой (8).
5. Покажем, что резонанс
третьего ранга в системе (4) возникает при 
. Поступая аналогично предыдущему случаю, найдем
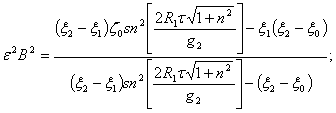(21)
где 
а
модуль функции синус-амплитуды 
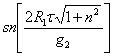есть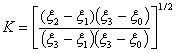 
.
Период колебаний по 
определяется
выражением (20), где вместо 
нужно взять К.
Пример. Рассмотрим нить со следующими
параметрами: 
Начальные условия примем следующими:
при
На рис. 2 и 3 показаны огибающие
амплитуд резонансных поперечных и угловых колебаний нити, построенные согласно
формулам (18) и (21). Из графиков видно, что в системе происходит периодический
энергообмен между обобщенными координатами, причем огибающие амплитуд
резонансных колебаний представляют собой эллиптические функции времени довольно
большого периода.
Полученные решения создают достаточно
ясное представление о своеобразных резонансных колебаниях нити при отсутствии
внешнего воздействия. Эти резонансные режимы колебаний не представляют собой простых
изолированных явлений, так как зависят от начальных условий.
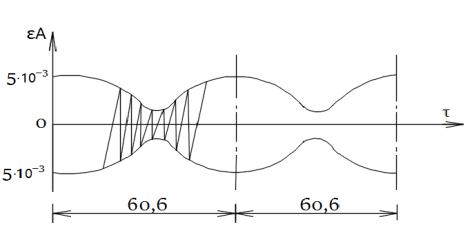
рис. 2.
Огибающая амплитуд поперечных колебаний нити
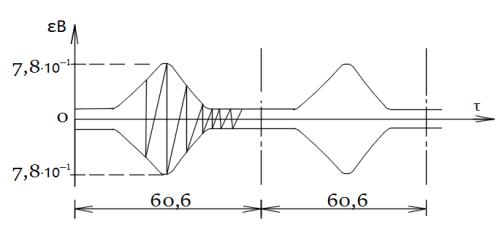
рис. 3.
Огибающая амплитуд угловых колебаний нити
Cписок использованных источников:
1. В. А. Ивович Взаимосвязь
при колебаниях виброизолированных систем.
«Строительная механика и расчет сооружений» , 1971, № 2.
2. Э. В. Бубнович
«Резонансные колебания гибкой нити при случайных воздействиях». II Международная
межвузовская научно-практическая конференция, №2, Бишкек, 2014.
3. R. A. Struble Nonlinear
Differential Equations, McGraw Hill, New York, 1
962.
4. R. W. Evan-Jwanowski “On the
Parametric Response of Structures”, Applied Mechanics Review, vol. 18, NO. 9,
Sept., 1965.
5.
Н.
Н. Боголюбов, Ю. А. Митропольский Асимптотические методы в теории нелинейных
колебаний. М., Физматгиз, 1965.