Янковська О.М.

Національний технічний університет України «Київський політехнічний інститут»

ГРАФІЧНИЙ МЕТОД РОЗПОДІЛУ АКТИВНИХ І РЕАКТИВНИХ СТРУМІВ

Графічний метод знаходження найбільш економічного розподілу активних і реактивних струмів між паралельно працюючими агрегатами або установками, враховуючи зміну вартості електроенергії. За цим методом вихідною для вирішення задач є векторна діаграма струмів двох агрегатів або установок, паралельно працюючих на одного споживача. Струм споживача задається за величиною і напрямом. Геометрична сума струмів установок повинна бути рівною геометричній сумі струмів споживача; вони можуть мати довільні величини і напрями. Точка, яка визначає однозначний розподіл струмів установок, може займати будь-яке положення. Завдання можна сформулювати таким чином: «знайти графічно точку струморозподілу, в якій сума витрат виробництва і передачі для обох струмів буде мінімальною, використовуючи заданий струм споживача,».

Для будь-якого положення точки струморозподілу можна безпосередньо визначити витрати виробництва та розподілу струму при відповідних геометричних побудовах (рис.1 і 2).

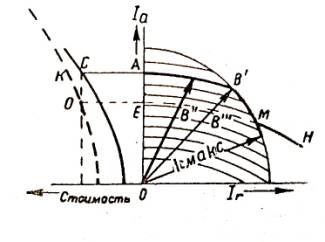
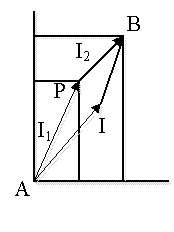
Рис.1 Рис.2

На осі абсцис нанесені реактивні струми. На осі ординат - активні струми. Для струму ОВ, точно так само як і для струму ОВ₁, можна однозначно визначити витрати. Точки рівних витрат з'єднані кривою і таким чином, можна отримати сімейство кривих рівних вартостей.

Векторам ОВ, OB' і OA, кінці яких лежать на одній кривій, відповідає однакова величина витрат виробництва струму. Для випадку однієї машини струм ОА відповідає витратам АС . Для двох машин потрібно більше витрат – АК більше АС. Якщо число машин збільшується, то криві рівних витрат отримають суміщення часткових кривих.

Розглянемо випадок паралельної роботи двох установок: a і b на загального споживача (рис.2). Для а нульова точка знаходиться в А. Для вектора АР витрати – 42 в.о. В - нульова точка для установки b (криві перевернуті на 180). Для вектора BP витрати – 59 в.о. Сумарні витрати – 101 в.о., тобто стільки потрібно витратити, щоб отримати вектор АВ, якщо Р – точка струморозподілу.

Якщо точка зміститься в D, тоді відповідні вартості будуть 68 і 49 в.о.. Сумарні витрати 112 в.о., тобто на 10 % вище.

Мінімум знаходиться в точці Р, точці найбільш економічного розподілу активних і реактивних струмів .

Якщо точка зміститься в Е, то установка покращує свій cosφ, але зростають витрати (76+42=124 в.о). Якщо вихідною умовою є рівність cosφ установок, то відносний мінімум буде в деякій точці С по лінії АВ .

Можна побудувати криві не по точках, а виконавши аналіз витрат виробництва.

Складаємо рівняння:

Окремі членами цього рівняння є відповідно: змінні втрати, потужність споживача і постійна механічна потужність. Оскільки і відповідно активні і реактивні складові струму, то рівняння записується у вигляді:

,

а в іншій формі:

,

тобто отримуємо рівняння кола з координатами і .

Отже, криві рівних витрат – кола. Кола концентричні. Центр М отримуємо (рис.4), знаючи напругу і опір. Коло радіуса МВ відразу дає вектор ОА активного струму, для якого можна визначити на кривій величину витрат. Для визначення витрат двох паралельно працюючих установок (рис.5) застосовується така побудова: центр одного сімейства кривих М₁, центр іншого сімейства кривих М₂. Витрати для G отримаємо, якщо навколо М проведемо коло радіусів M₁G, і тоді АС₁ еквівалентний AG. Аналогічно ВС₂ еквівалентний BG з витратами С₂D₂ . Сума витрат для G дорівнює С₁D₁+C₂D₂. Пряма М₁М₂ є геометричним місцем точок дотику двох кіл. Точки мінімуму слід шукати на цій прямій.

Інший спосіб – переміщення кривої К₂ витрат установки b паралельно до самої себе. Точка дотику з K₁ визначить точку Р струморозподілу. Місце розташування точки Р залежить від кривизни лінії витрат. Положення точки Р майже не впливає на співвідношення АН; НЕ і, отже, , тобто розподіл реактивних струмів між двома станціями залежить від електричних величин, але не від витрат, оскільки неважко довести, що нахил прямої M₁M₂ залежить від електричних параметрів.

Розподіл активних струмів ВН₁ і ЕH₁ в основному залежить від кривих витрат, але не від електричних величин.

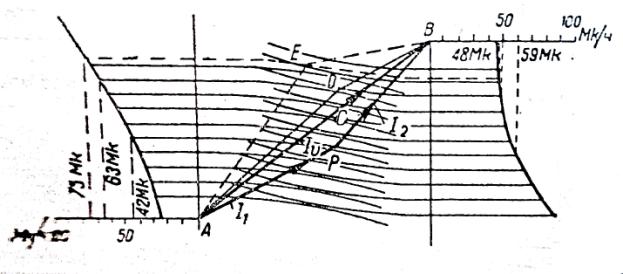
Рис.3

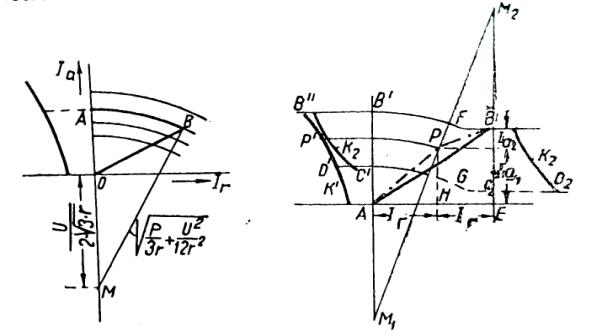
Рис.4 Рис.5

У разі паралельної роботи генератора а і двигуна b через опір r₁ і r₂ на загального споживача розподіл отримуємо таким чином (рис.9): відрізок АМ₁ отримаємо за напругою споживача та опору r_а. Аналогічно отримаємо ВМ₂ Якщо b не працює, то струм АВ еквівалентний АС як радіус кола, проведеного через b навколо центру М₁. Для b втрати холостого ходу представлені відрізком Bh, чим і визначається коло hEF радіусом М₂Е₁ центр сторін М₂.

Найбільш економічний розподіл навантажень при паралельній роботі а і b представлений точкою перетину Е кола холостого ходу з прямою М₁М₂

Рис.6.

Введення двигуна b зменшує витрати на величину, відповідну СС; з цієї економії необхідно відрахувати постійні витрати виробництва в установці b. Коефіцієнт потужності зріс від cosφ до cosφ₁. Подальше збільшення cosφ приведе до зменшення економії. Для точки F вона дорівнює 0. Величина найбільш економічного зсуву фаз визначається не характеристикою b, а характеристикою АВ, АМ₁, ВМ₂, тобто параметрами споживача та мережі.

Розглянемо випадок (рис. 7), коли кожна з двох установок працює на свого споживача і в той же час пов'язані між собою. Струм споживача представлений відрізком АС, споживача За відсутності зв'язку еквівалентні струми будуть відповідно АЕ₁ і ВЕ і витрати E₁F₁ і К₂F`₂.

Сумарні витрати 135 в.о. (85+50). Уведення зв'язку дає точку найвигіднішого розподілу D і струми і , геометрична сума яких дорівнює геометричній сумі і .

В з’єднувальній лінії протікає струм , еквівалентний для струмів . Активні струми відповідно дорівнюють АG₁ і ВG₂. Відповідно рівні G₁H₁ і G₂H₂. Сума витрат у цьому випадку дорівнює 120 в.о.. (50+70). Економія складає 10%, що є лімітом економічності з’єднувальної лінії.

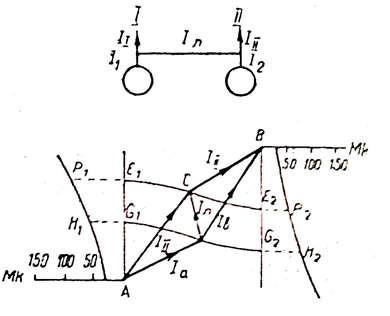
Рис.7