#Евтушенко Д.А., Одаренко Е.Н. Управление дисперсионными характеристиками фотонно-кристаллических волноводов

Физика/7. Оптика

Евтушенко Д.А., Одаренко Е.Н.

Харьковский национальный университет радиоэлектроники, Украина

Харьковский национальный университет имени В.Н. Каразина, Украина

Управление дисперсионными характеристиками фотонно-кристаллических волноводов

Фотонные кристаллы привлекают внимание исследователей благодаря их уникальным физическим свойствам [1]. Эти свойства описываются дисперсионными характеристиками, которые представляют собой зависимость частоты от фазовой скорости. Спектральные свойства фотонных кристаллов обусловлены структурной интерференцией в периодических системах и характеризуются наличием запрещенных и разрешенных частотных зон. Фотонная запрещенная зона (photonic band gap) представляет собой диапазон частот, в котором распространение света невозможно в фотонном кристалле во всех направлениях. Такие структуры могут иметь дефекты (линейные или локальные), за счет которых образуются волноводы и резонаторы.

Рассмотрим фотонно-кристаллический волновод, который формируется путем удаления одного ряда элементов из периодической структуры, сформированной бесконечными диэлектрическими цилиндрами (схема волновода представлена на врезке на рис. 1) с диэлектрической проницаемостью ε = 12.

Модификация данной линии передачи производится путем изменения конфигурации элементов фотонного кристалла, расположенных на границах волноводного канала. Численные расчеты дисперсионные диаграммы в данной работе производятся с помощью программного пакета MIT Photonic Bands (MPB) [2].

На рис. 1 приведена дисперсионная диаграмма для исходной конфигурации волновода. Данная диаграмма приведена для ТМ поляризации, поскольку в этом случае фотонный кристалл имеет полную запрещенную зону. В данном случае радиус сечения r=0,2. По оси ординат откладывается безразмерная частота, где с – это скорость света. По оси абсцисс – безразмерное волновое число. а – постоянная решетки.

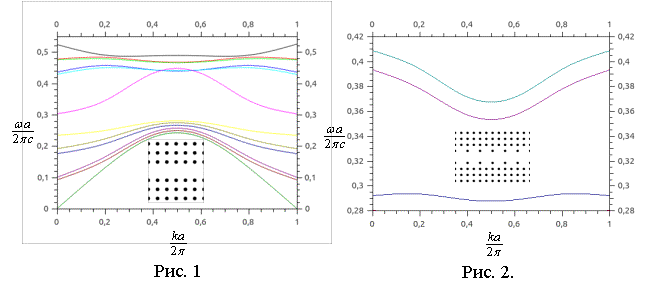
Фотонная запрещенная зона бесконечного фотонного кристалла без линейного дефекта расположена в интервале . Из рис. 1 видно, что в фотонной запрещенной зоне существует одна дисперсионная кривая (волновод является одномодовым).

Рассмотрим далее различные модификации этого волновода. На рис. 2 представлена дисперсионная диаграмма для конфигурации, показанной на врезке к этому рисунку. В данном случае на границе волноводного канала удалена часть элементов структуры. Данная диаграмма построена в пределах запрещенной зоны бесконечного фотонного кристалла. Из рисунка видно, что в запрещенной зоне находится три дисперсионных кривых. Следовательно, в данном случае волновод становится многомодовым. Кроме того, данный волновод имеет две полосы пропускания различной ширины.

На рис. 3 представлена дисперсионная диаграмма для волновода с другой конфигурацией границ канала. Здесь часть цилиндров на границе волноводного канала имеет не круглое, а квадратное поперечное сечение. Из рисунка видно, что спектральные характеристики такой структуры существенно отличаются от характеристик исходного варианта (рис. 1). В данном случае волновод имеет три частотные полосы пропускания.

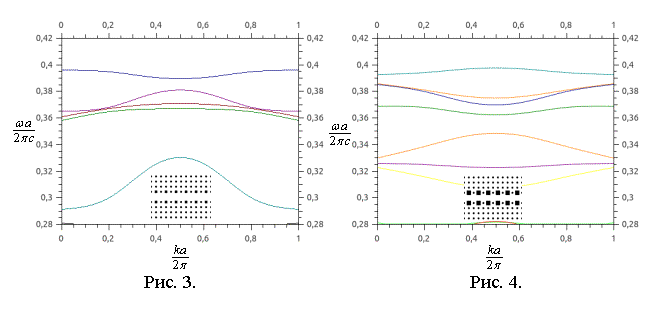
На рис. 4 представлена дисперсионная диаграмма для третьего варианта волновода. Как видно, характеристики значительно изменились по сравнению с предыдущим вариантом (рис. 3). В частности, возросло количество волноводных мод и полос пропускания.

Таким образом, результаты расчета дисперсионных характеристик фотонно-кристаллического волновода с различной конфигурацией элементов, расположенных на границе канала свидетельствуют о возможности управлять спектральными характеристиками данной структуры. В частности такой модифицированный волновод может иметь несколько полос пропускания в пределах запрещенной зоны бесконечного фотонного кристалла.

Литература:

1. Joannopoulos J.D., Meade R.D., Winn J.N. Photonic Crystals: Molding the Flow of Light. – Princeton Univ. Press, 1995. – 137 p.

2. Johnson S. G., Joannopoulos J. D. Block-iterative frequency-domain methods for Maxwell's equations in a planewave basis // Optics Express. – 2001, No 3. – pp. 173–190.