#Тетьора С.В., Трубачев С.І., Боронко О.О. Розрахунок ламінованої склом полімерної структури фотоелектричних модулів

Студ. Тетьора С.В., к.т.н., доц. Трубачев С.І., д.т.н., проф. Боронко О.О.

Національний технічний університет України

«Київський політехнічний інститут»

Розрахунок ламінованої склом полімерної структури фотоелектричних модулів

Вступ. В будівельній інженерії та автомобільній промисловості широко використовуються ламіновані плити з скляними зовнішніми шарами та основним шаром з полівінілбутирала(ПВБ) [1, 2]. Кристалічні або тонко плівкові фотоелектричні модулі, які зараз доступні на ринку, складаються з зовнішніх скляних або полімерних шарів і шару сонячних батарей, які вбудовані в полімерний наповнювач [3, 4, 5,]. Легка конструкція фотоелектричних модулів включає передню та задню панелі із пластмаси. 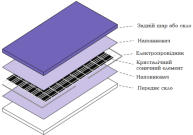Ці зовнішні шари з’єднані з прозорим поліуретаном(ПУР), який вбудовані сонячні батареї [6]. Рис. 1(а-в) ілюструє різні типи фотоелектричних модулів.

Для проектування скляних ламінатів і фотоелектричних модулів необхідно аналізувати придатність таких матеріалів, як ПВБ та етиленвінілацетат(ЕВА) для вбудовування сонячних батарей. Ці наповнювачі повинні компенсувати різні механічні та термічні деформації верхніх та нижніх шарів. Необхідно уникати розшаровування і сонячні батареї повинні бути захищені від вологи та повітря. Механічні властивості м’яких наповнювачів зазвичай страждають в процесі виготовлення. Крім того вплив навколишнього середовища може призвести до зміни механічних властивостей з плином часу. Тому надійна оцінка характеристик жорсткості можлива лише шляхом випробування прототипу, наприклад, згин балки або плити. Щоб оцінити результати випробувань необхідні надійні методи структурного аналізу, які стосуються глобального деформованого стану, наприклад, прогин, а також локального НДС, наприклад, напруження і деформації від прикладеного поперечного навантаження.

а	б	в

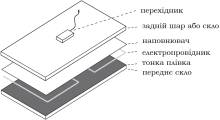
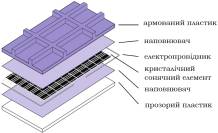
Рис. 1. Компоненти сонячного модуля: а) плівкового, б) легкого, в) кристалічного

Основною особливістю ламінованих склом фотоелектричних модулів, якщо порівнювати з «сандвічами» і ламінатами легких структур, є те, що вони мають жорсткі зовнішні шари і відносно податливий шар наповнювача. Нехай - модуль зсуву скляного зовнішнього шару і - модуль зсуву полімерного шару. Відношення модулів зсуву для матеріалів, які використовуються в сонячних батареях знаходяться в діапазоні від до , в залежності від виду полімеру і температури. Для класичного сандвіча використовується співвідношення, що знаходиться в діапазоні між і . Крім того, в класичній конструкції сандвіча зовнішні шари тонкі в порівнянні з ядром, а в сонячних батареях зовнішні шари товсті, а ядро дуже тонке.

В даній роботі представлені результати структурного експериментального аналізу та аналізу методом скінченних елементів ламінованих склом балок з основними шарами з різних полімерів, які використовуються в фотоелектричній промисловості.

Постановка задачі. Розглянемо вільно оперту ламіновану склом пластину (рис. 2) навантажену поперечною силою по центру.

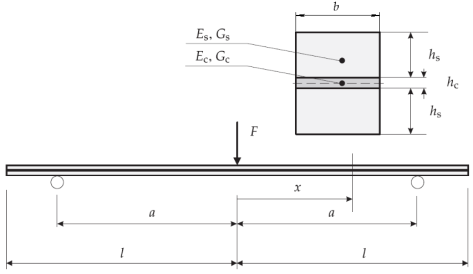
Рис. 2. Схема вільно опертої пластини

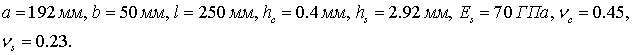Необхідно визначити максимальний прогин та напруження в кожному шарі.

Результати випробувань. В [7] були наведені значення максимального прогину при випробуваннях ламінованої склом пластини на трьох точковий згин(рис. 3) при різних значеннях поперечної сили .

Рис. 3. Трьохточковий згин

Аналіз методом скінченних елементів. Для скінченно-елементного аналізу використовувався програмний пакет FEMAP v11.1.0. За рахунок симетричності випробуваного зразка раціонально розглядати половину, закріплюючи переріз розсічення по нормалі. Для моделювання зразка було використано 12750 елементів типу PARA SOLID та 57790 вузлів. Дана модель має 8 елементів по товщині зовнішнього шару і 2 елементи по товщині основного шару. На рис. 4 зображено скінченно-елементну сітку, крайові умови та навантаження.

Рис. 4. Скінченно-елементна модель

На рис. 5 зображено розподіл напружень шарах деформовану пластини під дією та .

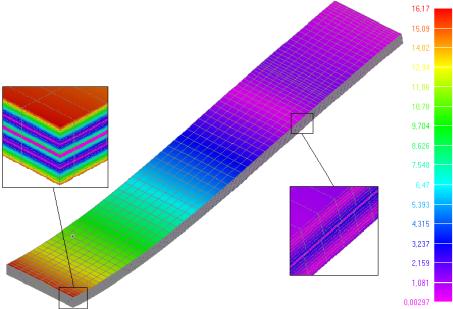
Рис. 5. Контурний графік напружень по Мізесу для та

Не важко бачити, що напруження в основному шарі дорівнюють нулю, тобто вся несуча здатність даної конструкції залежить від зовнішніх шарів.

Порівняння експериментальних значень максимального прогину та отриманих за допомогою численних методів наведено в на рис. 6.

Так як запропонована модель показала високу збіжність з експериментальними даними, то за допомогою методу скінченних елементів було визначено власні форми та частоти коливань ламінованої склом балки з основним шаром з ПВБ. Власні частоти наведені в таблиці 1.

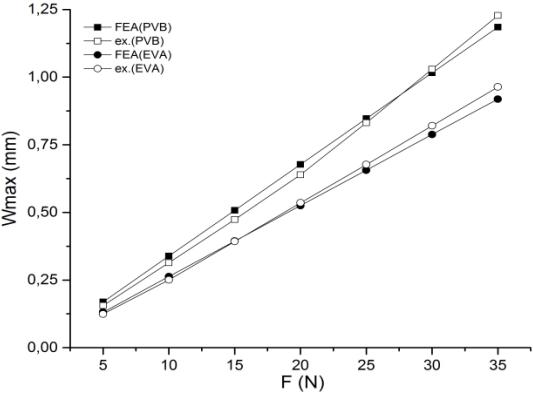
Рис. 6. Графіки залежності максимального прогину від сили для ПВБ ,) та ЕВА,)

Таблиця 1. Власні частоти коливань пластини з основним шаром з ПВБ

№	ω, Гц	№	ω, Гц
1	77,31435	6	697,9014
2	226,2717	7	1004,343
3	398,9698	8	1023,139
4	527,2266	9	1138,941
5	558,7838	10	1441,973

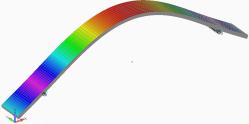
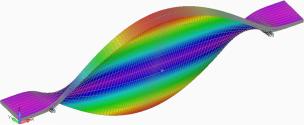
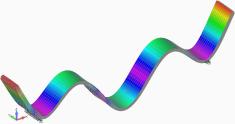
На рис. 7 зображені перші 6 власних форм коливань ламінованої пластини.

Рис. 7. Власні форми коливань ламінованої пластини

Висновки. В ході даної роботи була запропонована скінченно-елементна модель ламінованої склом пластини, сонячного модуля, з м’яким основним шаром. Дана модель показала високу збіжність з експериментальними даними для таких матеріалів, як ПВБ і ЕВА. Були визначені напруження та деформації в шарах пластини. Також були визначені власні частоти та відповідні форми коливань. Запропонована модель може бути використана при розрахунках та проектуванні фотоелектричних модулів сонячних батарей різних конфігурацій.

Список літератури

1. Y. Koutsawa, E. M. Daya, Static and free vibration analysis of laminated glass beam on viscoelastic supports, International Journal of Solids and Structures 44 (2007)

2. I. V. Ivanov, Analysis, modeling, and optimization of laminated glasses as plane beam, International Journal of Solids and Structures 43 (2006)

3. S.-H. Schulze, M. Pander, K. Naumenko, H. Altenbach, Analysis of laminated glass beams for photovoltaic applications, International Journal of Solids and Structures 49 (2012)

4. M. Paggi, S. Kajari-Schröder, U. Eitner, Thermomechanical deformations in photovoltaic laminates, The Journal of Strain Analysis for Engineering Design 46 (8) (2011)

5. M. Corrado, M. Paggi, A multi-physics and multi-scale numerical approach to microcracking and power-loss in photovoltaic modules, Composite Structures 95 (2013)

6. M. Weps, K. Naumenko, H. Altenbach, Unsymmetric threelayer laminate with soft core for photovoltaic modules, Composite Structures 105 (2013)

7. Schulze S, Pander M, Naumenko K, Altenbach H. Analysis of laminated glass beams for photovoltaic applications. International Journal of Solids and Structures (2012)