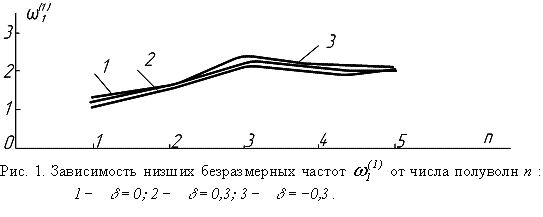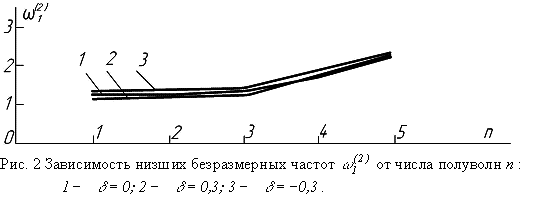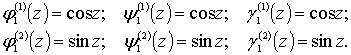Мельник В.Н., Карачун В.В., Заброда А.А., Лозовик Т.Н
Национальный технический университет Украины «КПИ»
ЛИНЕЙНО НЕЗАВИСИМЫЕ ПЕРЕМЕЩЕНИЯ ПОВЕРХНОСТИ КАК СЛЕДСТВИЕ
ПОСТОЯНСТВА PARTIALIS ЧАСТОТ
Осуществим
выбор функций 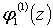 и
и 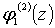 , функций
, функций 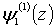 и
и 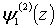 , а также функций
, а также функций 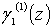 и
и 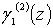 - в координатных
функциях оболочки, обеспечивающих их ортогональность:
- в координатных
функциях оболочки, обеспечивающих их ортогональность:
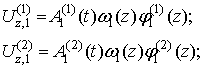
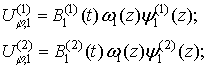
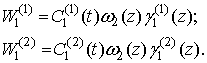
Основным
требованием в этой процедуре считаем выполнение условия линейной независимости
каждой пары. В остальном – произвольный выбор.
Для предварительных расчетов примем следующие значения:
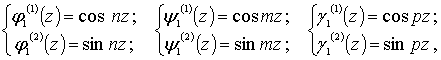 (1)
(1)
где ![]()
Конкретизируем задачу и вычислим значения парциальных частот для следующих
числовых характеристик:
![]()
![]() ;
;
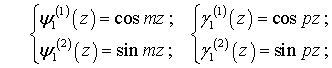
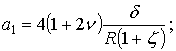
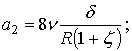
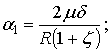
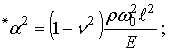
![]()
![]()
![]()
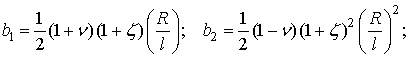
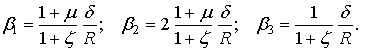
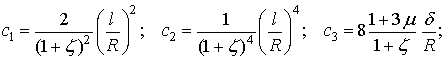
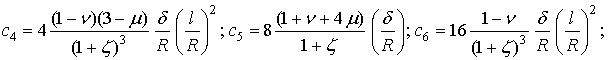
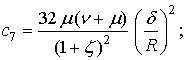
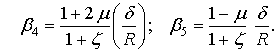
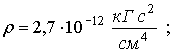
![]()
![]()
![]()
![]()
![]()
![]()
Остановимся подробнее
на выборе величины ![]() .
Пренебрегая упругой связью между уравнениями, частоты собственных колебаний
свободной оболочки в продольном направлении можно определить из соотношения
.
Пренебрегая упругой связью между уравнениями, частоты собственных колебаний
свободной оболочки в продольном направлении можно определить из соотношения
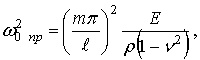
а для принятых числовых значениях
ее величина при ![]() будет равна:
будет равна:
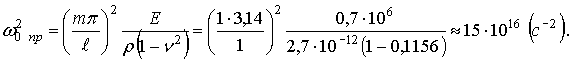
Величина ![]() выбрана из условия, что близкими к частотам
реальной оболочки будут лишь первые частоты.
выбрана из условия, что близкими к частотам
реальной оболочки будут лишь первые частоты.
Для тех же числовых
значений и геометрических параметров, частота поперечных колебаний будет равна:
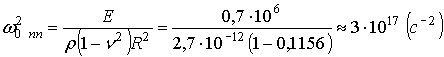 .
.
Частоту собственных
колебаний в окружном направлении примем
![]() .
.
Проведем обоснование
выбора параметров “n”, “m” и “p” в соотношениях (1). Для этого,
вычислим значения partialis
частот ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() в функции этих параметров.
в функции этих параметров.
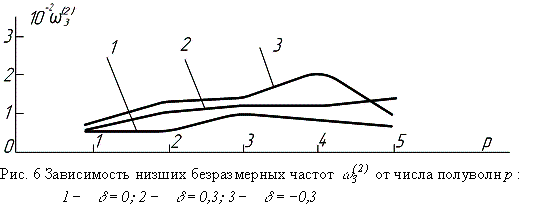
Ограничиваясь числом
полуволн не более 5, графики изменения partialis частоты ![]() представим на рис 1,
представим на рис 1, ![]() - на рис. 2,
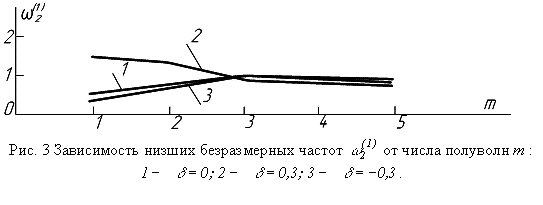
- на рис. 2, ![]() - на рис. 3,
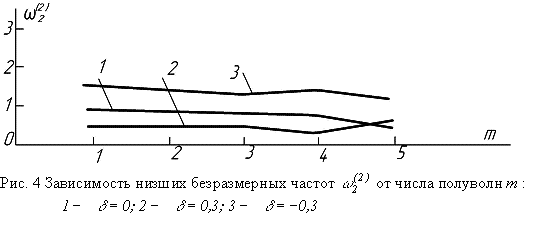
- на рис. 3, ![]() - на рис. 4,
- на рис. 4, ![]() - на рис. 5,
- на рис. 5, ![]() - на рис. 6.
- на рис. 6.
Как видно из рис. 1,
2, 3, partialis частоты по всем трем координатам
практически не изменяются с увеличением числа полуволн n, m , p. Поэтому
можно принять
![]() ,
,
что подтверждает
известный факт о наибольшем соответствии частотам реальной оболочки низших
парциальных частот. В этой связи, функции ![]() примут вид:
примут вид: