Технические науки/2. Механика
Бакиров
Ж.Б., Бакиров М.Ж., Михайлов В.Ф.
Карагандинский
государственный технический университет, Казахстан
Анализ нелинейных случайных колебаний
методом усреднения
Рассмотрим нелинейную систему, испытывающую
мультипликативные и аддитивные случайные воздействия
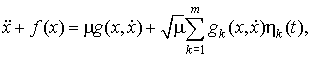
где
![]() — малый параметр;
— малый параметр; ![]() — нелинейная
восстанавливающая сила;
— нелинейная
восстанавливающая сила; ![]() ,
, ![]() — периодические
функции времени с периодом Т(а)=
— периодические
функции времени с периодом Т(а)=![]() ;
; ![]() — стационарные центрированные
случайные процессы с матрицей корреляционных функций
— стационарные центрированные
случайные процессы с матрицей корреляционных функций ![]() .
.
Для малых ![]() движение системы
близко к периодическому и решение может быть представлено в виде
движение системы
близко к периодическому и решение может быть представлено в виде
![]() ,
, ![]() , (2)
, (2)
где ![]() ,
, ![]() — «медленно»
меняющиеся функции.
— «медленно»
меняющиеся функции.
Введем новую переменную — энергию ![]() , определенную как первый интеграл порождающего уравнения (
, определенную как первый интеграл порождающего уравнения (![]() )
)
![]() ,
, 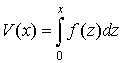 , (3)
, (3)
где ![]() — потенциальная энергия системы, причем
— потенциальная энергия системы, причем ![]() .
.
Для
порождающего уравнения a, ![]() , b являются постоянными. Тогда дифференцируя (2) по
времени, с учетом последнего выражения получим
, b являются постоянными. Тогда дифференцируя (2) по
времени, с учетом последнего выражения получим
![]() (4)
(4)
где мгновенная частота
колебаний
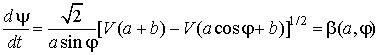 .
.
Усредняя эту частоту
можно записать
![]()
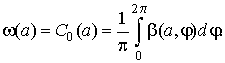 (5)
(5)
Подставляя
(2) и (4) в (1), после некоторых преобразований получаем следующую систему уравнений
в стандартной форме
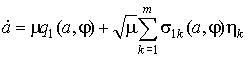 ,
,
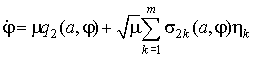 ,
(6)
,
(6)
в которых
![]()
![]() ,
,
где ![]() .
.
Поскольку
функции ![]() ,
, ![]() периодические, то для
фиксированного а они могут быть
разложены в ряд Фурье
периодические, то для
фиксированного а они могут быть
разложены в ряд Фурье
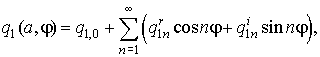
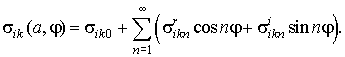 (7)
(7)
![]() (8)
(8)
где ![]() — белый шум с единичной интенсивностью;
— белый шум с единичной интенсивностью;
![]() и
и ![]() — усредненные
коэффициенты сноса и диффузии, определяемые по формулам
— усредненные
коэффициенты сноса и диффузии, определяемые по формулам
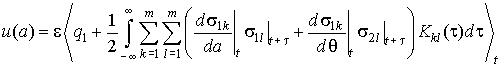 ,
,
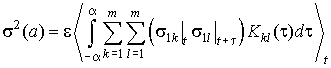 ,
(9)
,
(9)
![]() —
означает, что берется значение функций в момент времени t.
—
означает, что берется значение функций в момент времени t.
Используя для ![]() соотношение (5) и подставляя (7) в соотношения(9), получим
соотношение (5) и подставляя (7) в соотношения(9), получим
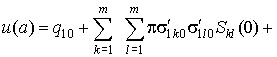
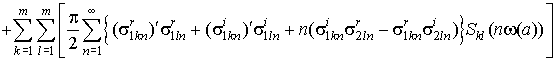
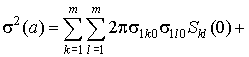
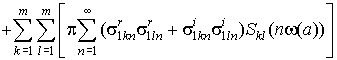 . (10)
. (10)
Здесь штрихи означают
производные по “a”, кроме того учтено, что
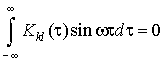 ,
, 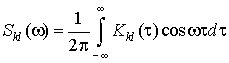
Стохастическому
уравнению Ито (8) соответствует следующее уравнение А.Н. Колмогорова
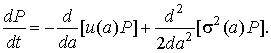
где
![]() – плотность
распределения амплитуды.
– плотность
распределения амплитуды.
Стационарное
решение этого уравнения имеет вид
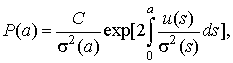 (11)
(11)
где С– нормированная постоянная, определяемая из условия нормировки
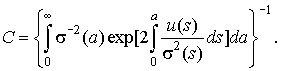
Из формулы преобразования плотности вероятности с
использованием (3) можно определить плотность распределения полной энергии
![]() (12)
(12)
Здесь амплитуда выражается
через Е из соотношения
![]() (13)
(13)
В
работе [Ошибка!
Источник ссылки не найден.] показано, что совместная плотность
распределения перемещения и его производной можно выразить через плотность
распределения полной энергии:
![]() (14)
(14)
где
период изменения энергии ![]() получается из
выражения
получается из
выражения ![]() с использованием (13)
и (5). Теперь из (14) можно определить одномерную плотность распределения
перемещения
с использованием (13)
и (5). Теперь из (14) можно определить одномерную плотность распределения
перемещения
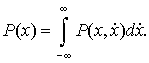
Исходя
из вышеизложенного предлагается следующий порядок расчета плотности распределения
выходных параметров:
1)
принимается множество значений a от нуля до
заданного максимального значения на малом интервале (что обусловлено
точностью);
2)
выбираются значения ![]() на равных интервалах от 0 до
на равных интервалах от 0 до ![]() ;
;
3)
для каждого значения ![]() из (5) с
использованием выражения для
из (5) с
использованием выражения для ![]() определяем
определяем ![]() и
и ![]() ;
;
4)
для каждого значения ![]() , используя БПФ определяем
, используя БПФ определяем ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для
для ![]() до
до ![]() (значение m должно выбираться в зависимости от отсечения
частоты из функции спектральной плотности воздействия);
(значение m должно выбираться в зависимости от отсечения
частоты из функции спектральной плотности воздействия);
5)
численным дифференцированием определяем производные ![]() ,
, ![]() ;
;
6)
по формулам (10) определяем коэффициенты сноса и диффузии ![]() ,
, ![]() ;
;
7)
по формуле (11) численным интегрированием вычисляем ![]() ;
;
8)
для каждого ![]() вычисляем
вычисляем ![]() ,
, ![]() и по формуле (12) вычисляем
и по формуле (12) вычисляем ![]() ;
;
9)
из (5) заменой ![]() на
на ![]() определяем
определяем ![]() и
и ![]() ;
;
10)
для различных сочетаний ![]() и
и ![]() по (3) определяем Е и по формуле (14) вычисляем
по (3) определяем Е и по формуле (14) вычисляем ![]() ;
;
11)
численным интегрированием (14) вычисляем ![]() .
.
В качестве примера рассмотрено уравнение Дуффинга с
нелинейным затуханием при внешнем и параметрическом случайном воздействии со
скрытой периодичностью. Эффективность метода показана сравнением результатов с
результатами прямого статистического моделирования. Расчеты в обоих случаях
проведены с использованием ПК MATLAB.
Предложенный метод позволяет получать адекватные результаты, как при широкополосных,
так и при узкополосных воздействиях.
Литература:
1. Dimentberg M., Gai G.Q., Lin Y.K. Application of quasiconservative
averaging to a nonlinear system under non white excitation // Int. J. Nonlinear
Mech. 30, 1995. p. 677-685.