М.П. Ленюк, Т.М. Олійник
Чернівецький
факультет НТУ „ХПІ”
МОДЕЛЮВАННЯ
ДИФУЗІЙНИХ ПРОЦЕСІВ В
НЕОДНОРІДНИХ СЕРЕДОВИЩАХ З М’ЯКИМИ МЕЖАМИ МЕТОДОМ ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО
ОПЕРАТОРА БЕССЕЛЯ – ФУР'Є – ЛЕЖАНДРА НА
ПОЛЯРНІЙ ОСІ ![]()
Моделювання
дифузійних процесів на тришаровій полярній осі ![]() з м’якими межами
математичного приводить до побудови обмеженого в області
з м’якими межами
математичного приводить до побудови обмеженого в області
![]()
розв’язку сепаратної системи диференціальних
рівнянь параболічного типу [1]
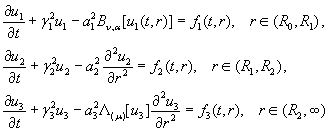 (1)
(1)
за початковими умовами
![]() (2)
(2)
крайовими умовами
![]() (3)
(3)
та умовами спряження
![]() (4)
(4)
У
рівностях (1) – (4) беруть участь диференціальні оператори Фур’є ![]() [2], Бесселя
[2], Бесселя ![]() [3], та Лежандра
[3], та Лежандра ![]()
![]() [4]; та
диференціальні оператори
[4]; та
диференціальні оператори
![]()
Припустимо,
що виконані умови на коефіцієнти:

Зауваження 1: Якщо ![]() то переходимо
до нових початкових умов
то переходимо
до нових початкових умов
![]()
Виберемо числа ![]() та
та ![]() із алгебраїчної
системи:
із алгебраїчної
системи:
![]()
![]()
Інтегральне
зображення аналітичного розв’язку дифузійної задачі (1) – (4) знайдемо методом
гібридного інтегрального перетворення із спектральним параметром, породженого
на множині ![]() гібридним
диференціальним оператором (ГДО)
гібридним
диференціальним оператором (ГДО)
![]() (5)
(5)
![]() - одинична функція
Гевісайда [5].
- одинична функція
Гевісайда [5].
Оскільки
ГДО ![]() самоспряжений й має
одну особливу точку
самоспряжений й має
одну особливу точку ![]() , то його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр
, то його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр ![]() .
.
Йому відповідає спектральна
векторна функція
![]()
При
цьому функції ![]() повинні задовільняти диференціальні рівняння
повинні задовільняти диференціальні рівняння
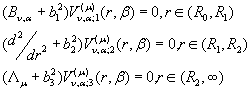 (6)
(6)
за крайовими умовами
![]() (7)
(7)
та умовами спряження
![]() (8)
(8)
У
рівностях (6) – (8) прийняті позначення:

Зауваження 2: Якщо ![]() , то ми приходимо до випадку, коли межі області жорсткі по
відношенню до відбиття хвиль.
, то ми приходимо до випадку, коли межі області жорсткі по
відношенню до відбиття хвиль.
Фундаментальну систему розв’язків
для диференціального рівняння Бесселя ![]() складають функції Бесселя першого
роду
складають функції Бесселя першого
роду ![]() та другого роду
та другого роду ![]() [3], фундаментальну систему розв’язків для диференціального
рівняння Фур’є
[3], фундаментальну систему розв’язків для диференціального
рівняння Фур’є ![]() складають тригонометричні функції
складають тригонометричні функції ![]() та
та ![]() [2]; фундаментальну систему розв’язків для диференціального
Лежандра
[2]; фундаментальну систему розв’язків для диференціального
Лежандра ![]() складають узагальнені приєднані
дійсні функції Лежандра
складають узагальнені приєднані
дійсні функції Лежандра ![]() та
та ![]() [4].
[4].
Наявність фундаментальної системи
розв’язків дозволяє знайти структуру функції ![]() у вигляді лінійної
комбінації функцій, які утворюють фундаментальну систему розв’язків [2]:
у вигляді лінійної
комбінації функцій, які утворюють фундаментальну систему розв’язків [2]:
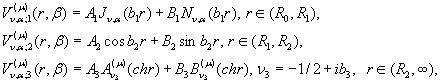 (7)
(7)
Крайова
умова в точці ![]() та умови спряження
(8) для визначення шести величин дають алгебраїчну систему з п’яти рівнянь:
та умови спряження
(8) для визначення шести величин дають алгебраїчну систему з п’яти рівнянь:
![]()
![]() (10)
(10)
![]()
У системі (10) беруть участь функції:
![]()
![]()
![]()
![]()
![]()
![]()
Візьмемо
![]() , де
, де ![]() підлягає визначенню. Перше рівняння системи стає тотожністю.
підлягає визначенню. Перше рівняння системи стає тотожністю.
Розглянемо
алгебраїчну систему стосовно ![]() :
:
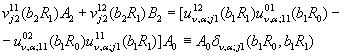 (11)
(11)
Визначник
системи (11)
![]()
Алгебраїчна система (11) має єдиний розв’язок [5]:
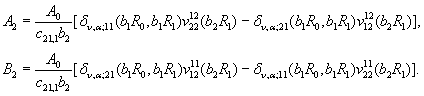 (12)
(12)
При відомих ![]() розглянемо
алгебраїчну систему стосовно
розглянемо
алгебраїчну систему стосовно ![]() та
та ![]() :
:
![]() (13)
(13)
Тут прийняті позначення:
![]() ,
,
![]()
Визначник алгебраїчної системи (13)
![]()
![]()
![]()
![]() - гама функція Ейлера
[6].
- гама функція Ейлера
[6].
Алгебраїчна система (13) має єдиний розв’язок [5]:
![]() (14)
(14)
![]()
Підставимо в рівності (9)
визначені формулами (12) та (14) величини ![]() та
та ![]() . Одержимо:
. Одержимо:
![]()
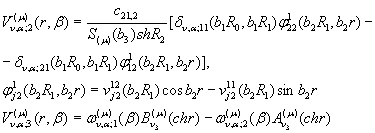 (15)
(15)
Отже, спектральна функція ![]() визначена.
визначена.
Визначимо величини
![]()
вагову функцію
![]() (16)
(16)
та спектральну щільність
![]() (17)
(17)
Наявність
спектральної вектор-функції ![]() , вагової функції
, вагової функції ![]() та спектральної щільності
та спектральної щільності
![]() дозволяє визначити пряме
дозволяє визначити пряме ![]() та обернене
та обернене ![]() гібридне інтегральне
перетворення , породжене на множині
гібридне інтегральне
перетворення , породжене на множині ![]() ГДО
ГДО ![]() [7]:
[7]:
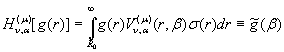 , (18)
, (18)
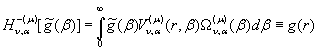 (19)
(19)
В основі розв’язання поставленої задачі
знаходиться основна тотожність інтегрального перетворення ГДО ![]()
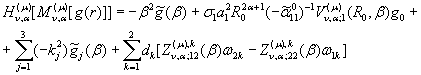 (20)
(20)
У рівності (20) прийняті
позначення:
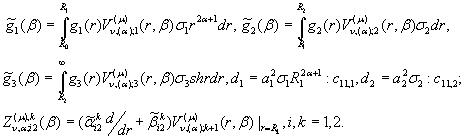 ,
, ![]()
Одержані формули (18) –
(20) складають математичний апарат для розв’язання поставленої задачі (1) –
(4).
Доведення тотожності (22) проводиться стандартним методом [6].
Розв’язання задачі.
Запишемо
систему (1) та початкові умови (2) в матричній формі:
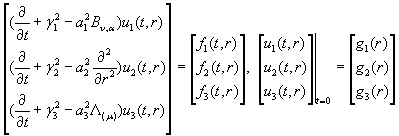 (21)
(21)
Інтегральний оператор ![]() згідно формули (18)
зобразимо у вигляді операторної матриці-рядка:
згідно формули (18)
зобразимо у вигляді операторної матриці-рядка:
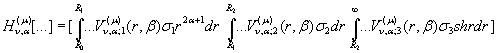 (22)
(22)
Застосуємо операторну матрицю-рядок (22) за правилом множення
матриць до задачі (21). Внаслідок основної тотожності (20) маємо задачу Коші
[2]:
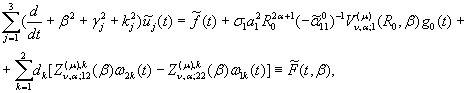
![]() (23)
(23)
Припустимо, що ![]() . Покладемо
. Покладемо ![]() ,
, ![]() ,
, ![]() .
.
Задача Коші (23) набуває вигляду найпростішої задачі Коші [2]:
![]() , (24)
, (24)
Розв’язком задачі Коші (24) є функція
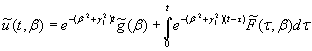 (25)
(25)
Інтегральний оператор ![]() згідно правила (19)
як обернений до (22) зобразимо у вигляді операторної матриці-стовпця:
згідно правила (19)
як обернений до (22) зобразимо у вигляді операторної матриці-стовпця:
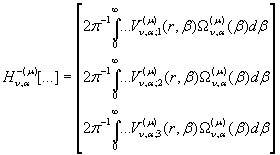 (25)
(25)
Застосуємо до матриці-елемента ![]() за правилом множення
матриць операторну матрицю-стовбець (25)
за правилом множення
матриць операторну матрицю-стовбець (25)
Одержуємо розв’язок
дифузійної задачі (1) – (4):
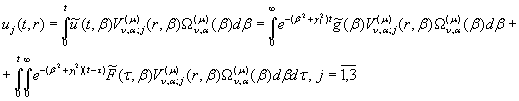 (26)
(26)
Введемо до розгляду
головні розв’язки дифузійної задачі (1) – (4): 1) породжені неоднорідністю
системи (1) (або початкових умов (2)) функції впливу
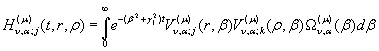 (27)
(27)
2) породжені крайовою
умовою в точці ![]() функції Гріна
функції Гріна
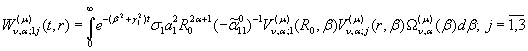 (28)
(28)
3) породжені
неоднорідністю умов спряження функції Гріна
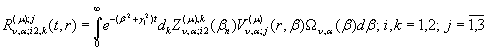 (29)
(29)
У результаті виконання низки
елементарних перетворень отримуємо інтегральне зображення аналітичного
розв’язку дифузійної задачі (1) – (4):
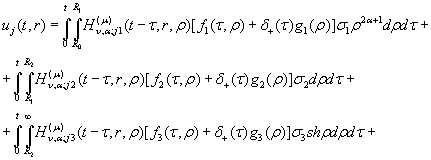
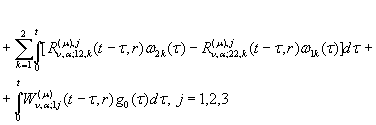 (30)
(30)
Тут ![]() - дельта-функція,
зосереджена в точці
- дельта-функція,
зосереджена в точці ![]() [8].
[8].
Зауваження 1. Якщо ![]() , то
, то ![]()
![]() і замість
і замість ![]() стоятиме
стоятиме ![]() . Якщо
. Якщо ![]() , то
, то ![]()
![]() і замість
і замість ![]() у формулах (27) –
(29) стоятиме вираз
у формулах (27) –
(29) стоятиме вираз ![]() .
.
Зауваження 2. Структура головних розв’язків задачі (1) – (4) допускає
безпосереднім вибором параметрів одержувати в рамках даної моделі будь-який
частковий випадок.
Зауваження
3. Інтегральне зображення (30) аналітичного
розвязку задачі (1) – (4) носить алгоритмічний характер. Це дозволяє
використовувати його як в теоретичних дослідженнях, так і в інженерних
(числових) розрахунках.
Література:
1.
Тихонов А.Н., Самарский
А.А. Уравнения математической физики. – М.: Наука, 1972. – 735с.
2.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468с.
3.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев,
1983. – 62с. – (Препринт / АНУССР. Ин-т Математики; 83-3).
4.
Конет І.М., Ленюк М.П. Інтегральні
перетворення типу Мелера – Фока. – Чернівці: Прут, 2002. – 248с.
5.
Курош А.Г. Курс высшей алгебры.- М.: Наука, 1971. – 432с.
6.
Градинштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. –
М.: Наука, 1971. – 1108с.
7.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є,
Бесселя, Лежандра). Частина 1. – Тернопіль: Економ. думка, 2004 – 368с.
8.
Шилов Г.Е.
Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328с.