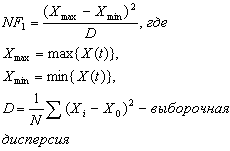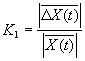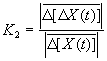Автоматическая классификация сигналов при контроле режущего инструмента

Технические науки/12. Автоматизированные системы управления на производстве

Сорокин В.В., Дараган А.Ф.

Северо-Казахстанский государственный университет им. М.Козыбаева, Казахстан

Автоматическая классификация сигналов при контроле режущего инструмента

Важной причиной снижения точности при механической обработки является изменение геометрических параметров детали вследствие износа режущего инструмента.

Следовательно, актуальной задачей является создание интеллектуальной системы контроля с прогрессивным методом обработки сигнала для получения информации о процессе особенно высокотехнологичной обработке.

При разработке интеллектуальных средств контроля возникает необходимость в автоматическом разделении исходной группы сигналов на некоторое количество классов, объединяющих, попавшие в них реализации, по определенному качественному признаку, в данном случае предлагается по дефектам режущего инструмента [1].

В статье описана методика и алгоритм автоматической классификации сигналов, основанная на теории идентификационных шкал.

Теория идентификационных шкал обосновывает возможность построения порядковых шкал как для распределений мгновенных значений (РМЗ) [2] сигналов, так и для распределений их временных интервалов (РВИ) [3,4].

Идентификационные шкалы (ИШ) отображают множество чисел, например, временной ряд наблюдений, объема N, в одно число – идентификационный параметр (IdP), с присоединением к нему качественной характеристики в виде имени распределения (I).

Имена распределений и связанные с ними, численные оценки идентификационных параметров образуют реляционную базу данных (БД). Управление такой БД состоит в пересортировке первоначального списка имен и их фильтрации. При упорядочивании чисел (IdP) автоматически ранжируются имена (I) и, соответственно, те свойства объекта или процесса, которые эти имена и числа представляют.

Таким образом, в ИШ происходит объединение технологии измерения и технологии БД для решения задач распознавания образов.

Предлагаемый алгоритм (рисунок) классификации сигналов использует идентификационные параметры, математические модели и физический смысл которых представлены в таблице 1.

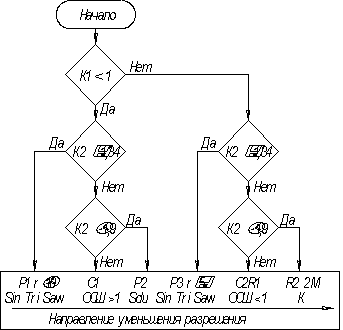
Рисунок - Алгоритм классификации сигналов

На основе данных моделей был разработан виртуальный прибор (ВП), в котором исходный, непрерывный во времени сигнал X(t) представляется, после аналого-цифрового преобразования, в виде дискретной выборочной реализации, объема N, и записывается в память компьютера.

Анализ значений идентификационных параметров позволяет определить – по какому из девяти направлений (от P1до R2) фильтруется данная запись. Каждое направление имеет свой собственный адрес. Адрес образуется путем перечисления единиц и нулей, соответствующих выполнению условий

(Да → «1», Нет → «0»). Разрядность адреса определяет «длину пути» прохождения анализа. Если разрядность адресов всех выходных направлений одинакова, то подобный алгоритм будем называть алгоритмом с равномерной дискретизацией (квантованием) свойств.

Таблица 1 - Модели идентификационных параметров

п/п	Имя IdP	Обозн. IdP	Физический смысл IdP	Математическая модель
1	Виртуальный объем	NF	Измерение формы распределения мгновенных значений сигнала X(t)	(Х_max-X_min) – размах сигнала N- объем выборки
2	Коэффициент вариабельности	K-1	Измерение среднего значения относительной скорости сигнала
3	Коэффициент вариабельности	K-2	Измерение среднего значения относительного ускорения сигнала
4	Коэффициент связи	M	Коэффициент характеризирующий связь между частотно-временными распределениями скорости и ускорения

Если в БД имеется множество записей, идентификационные параметры которых полностью покрывают диапазоны возможных значений IdP{4≤NF≤2N; 0≤(K1, K2)≤2}, то такую БД будем называть представительной. Сигналы, на основе анализа которых формируется представительная БД, называются эталонами БД.

Подразумевается, что для эталонов известны не только оценки их идентификационных параметров, но также другие характеристики, в том числе и качественные.

Рассмотрим технологию работы алгоритма, состоящую из двух этапов.

Первый этап заключается в создании эталонной БД и фиксации фильтрующих свойств. В таблице 2 для примера показан фрагмент БД, соответствующий реализации двух условий (K1<1 → Да, NF<=4 → Да, адрес направления P1→ 11) алгоритма.

Второй этап состоит в распознавании образцов сигналов, которые отсутствуют в начальной БД.

Таблица 2 - Фрагмент сортированной по параметру K1 БД (первые 4 столбца) и список имен сигналов (вторые 4 столбца), отфильтрованных алгоритмом по направлению Р1

№	FileName	K-1	K-2	№	FileName	K-1	K-2
17	squ-1	0,00002	1,00002	48	tri 1	0,00008	0,00004
34	sin 1	0,000063	0,000063	34	sin 1	0,000063	0,000063
47	cos 1	0,000063	0,000063	47	cos 1	0,000063	0,000063
48	tri 1	0,00008	0,00004	49	tri 10	0,0008	0,0004
61	saw 1	0,00008	1,00002	35	sin 10	0,000628	0,000628
18	squ-10	0,00038	1,900038	46	cos 10	0,000628	0,000628
35	sin 10	0,000628	0,000628	50	tri100	0,008	0,004
46	cos 10	0,000628	0,000628	36	sin100	0,006283	0,006283
49	tri 10	0,0008	0,0004	45	cos100	0,006283	0,006283
60	saw 10	0,0008	1,00011	51	tri1000	0,08	0,040001
89	gaus+tri100	0,008399	0,934698	59	Saw100	0,007992	1,001011

Анализ выходного состояния БД показывает, что:

· По направлению P1 фильтруются исключительно периодические сигналы прямоугольной (Squ) формы с числом периодов от 1 до 25000, что соответствует разрешению r>=4 (N=100000). Эта часть БД представляет идеальное ее состояние.

· Возможность фильтрации «посторонних» записей связана с введением дополнительного условия по идентификационному параметру, отличному от K1, K2.

Предложенный алгоритм имеет иерархическую классификационную структуру, отличающуюся от известных подобных построений тем, что она допускает «послойную» детализацию с делением групп на подгруппы причем, внутри каждого слоя наблюдается упорядоченность описаний по «горизонтали», что способствует детальному анализу сигналов поступающих от режущего инструмента.

Литература

1. Лоладзе Т.Н., Прочность и износостойкость режущего инструмента. - М.: Машиностроение, 1982, 320с.

2. Кликушин Ю.Н. Классификационные шкалы для распределений вероятности Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2000 г.

3. Гуменюк А.С., Данилюк Р.В., Кликушин Ю.Н., Виртуальный прибор для исследования эволюции аддитивной смеси сигнал-шум. Материалы 5-ой МНТК "Динамика систем, механизмов и машин». Кн.1, ОмГТУ, Омск,2004, с.373-376.

4. Кликушин Ю.Н., Кошеков К.Т. Модель роста популяции в задаче автоматической классификации сигналов.- Омский Научный Вестник, ОмГТУ, Омск, №4(33), 2005, с.160-163.