Технічні науки/
Галузеве машинобудування
К.т.н. Вольчев А.В.
Одесский национальный морской университет
Оценка долговечности деталей стрещинами
Для оценки остаточного ресурса объектов с
трещинами используются энергетические, деформационные и силовые критерии линейной
механики разрушения [1; 3], которые хотя и не отражают в должной мере кинетики
самого процесса разрушения, но удовлетворительно описывают чувствительность к
перегрузкам, надрезам и трещинам.
Трещины существенно изменяют напряженное
состояние объекта. Вопрос о напряженном состоянии в вершине трещины является достаточно
сложным в связи с возникновением там больших деформаций, лежащих за пределами упругости
[1; 3]. Изначальные дефекты в виде трещин, возникновение трещин в процессе
нагружения, их рост и распределение играют важную роль в оценке срока службы.
Разрушение определяется локальным напряженным состоянием в вершине трещины [1;
2; 3]. Основное положение механики разрушения состоит в том, что лавинное
разрушение происходит тогда, когда коэффициент интенсивности напряжении достигает
критической величины, зависящей от многих факторов. По существу расчет на
прочность о учетом сопротивления хрупкому разрушению — это расчет на
сопротивление распространению тре-
щины.
Между скоростью роста трещины и
коэффициентом интенсивности напряжений существует определенная зависимость. В
общем случае можно принять, что скорость распространения трещины пропорциональна
некоторой степенной функции от коэффициента интенсивности напряжений 
, где 
и 
— постоянные, определяемые
экспериментально. Коэффициент интенсивности
напряжений 
, где 
—напряжение, отнесенное к оставшемуся сечению
(нетто—напряжение); 
—глубина трещины, измеренная по нормали к ее фронту.
Для изотропного, вязкого и однородного
материала можно условно принять, что усталостная трещина в цилиндрическом
объекте диаметром д. распространяется равномерно по сечению к его центру, так
что максимальная ее глубина равна сумме глубин двух трещин, развивающихся с
диаметрально противоположных сторон, и может достигнуть диаметра. Тогда 
, где 
— исходный уровень
напряжения.
.
Введем
обозначение 
. После несложных преобразований получим 
.
Интегрируя последнее выражение в пределах
от 0 до 
, можно определить долговечность до образования трещины
глубиной 
:
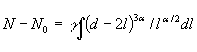. (1)
Подынтегральная функция не может быть
представлена элементарными функциями ввиду неопределенности показателя степени 
. Используя тождественные преобразования, выражение (1) можно
привести к виду
,
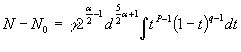где
; 
. Полученный интеграл представляет собой неполную
бета-функцию, а все выражение приводится к виду
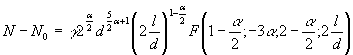
или
.
Количество
членов ряда, стоящего под знаком суммы, можно принять равным 5—6, так как этот
ряд является быстросходящимся. Тогда
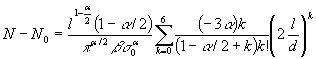. (2)
Если в выражение (2) подставить значение
критической глубины трещины 
, с которого начинается нестабильное ее развитие, то получим
ресурс долговечности от образования трещины до окончательного разрушения
детали.
Долговечность от начала нагружения до
окончательного разрушения определяется по кривой усталости. Следовательно,
можно получить уравнение кривой образования трещин усталости, предварительно
обозначив Ф правую часть выражения (2):
,
где
C и m — параметры уравнения
кривой усталости.
Последующая задача сводится к определению
параметров 
, 
, C, m и критической глубины
трещины 
.
Поиск аналитического определения
параметров 
и 
затруднителен из-за ограниченности
экспериментальных данных.
На основе сделанного ранее предположения
можно записать следующее выражение для напряжения в момент достижения трещиной критического
значения глубины: 
. Критическое значение коэффициента интенсивности напряжений
.
Аналитическое решение этого уравнения
относительно 
при известных 
, 
и 
затруднено. Но
решение его численными методами несложно. Если известен интервал, в котором
находится решение (0; 0,5
), то можно применить метод Ньютона (метод касательных),
согласно которому 
, где 
и 
— предыдущее и
последующее приближение к решению
уравнения 
; 
- первая призводная
функции 
[4, 5]. В
рассматриваемом случае
;
.
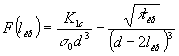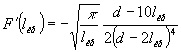Окончательно имеем
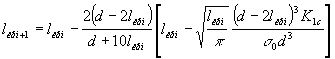. (3)
Расчет по формуле (3) прекращается при
выполнении неравенства 
, где 
— наперед заданная
точность вычислений.
Для определенных размеров объектов при
известных прочностных характеристиках их материалов можно построить кривые «критическое
значение глубины трещины — долговечность для развития трещины до этих
размеров».
По формуле (3) были просчитаны
критические размеры трещины для образцов (d = 7,5 мм из сталей 45 и
12Х18Н10Т, которые сравнивали с экспериментальными. Критическое значение коэффициента
интенсивности напряжений подсчитывали по формуле
,
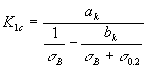где
и 
—коэффициенты регрессии, 
и 
—пределы
прочности и текучести материала.
Расхождение расчетных и экспериментальных
данных в наихудшем случае было менее 11 %, что указывает на приемлемость полученного
рекуррентного выражения для определения критических размеров трещины. Роль
агрессивности сред в формуле (3) отражается соответствующими коэффициентами интенсивности
напряжений, данные по которым постепенно накапливаются. Аналогичная задача для
объектов со сложной формой сечения еще не имеет решения.
Список
литературы
21. Екобори Т. Научные основы прочности и
разрушения материалов —К.: Наук. думка, 1978. — 352 с.
27. Коллинз Дж. Повреждение материалов в
конструкциях: Анализ. Предсказание. Предотвращение / Пер. с англ; Под ред. Э.
И. Григолюка.—М.: Мир, 1984.— 624с.
32. Махутов Н. А. Деформационные критерии
разрушения и расчет элементов конструкций на прочность-— М.: Машчностроение,
1981.— 270 с.
55. Поллард Дж. Справочник по
вычислительным методам статистики.— М.: Финансы и статистика, 1982.— 345с.
69 Форсайт Дж., Молер К. Машинные методы
математических вычислений.— М.: 1980.— 280 с.