Математика / 5. Математическое моделирование
К.т.н. Никонов В.В.
Самарский государственный
аэрокосмический университет, Россия
Лагранжев
метод для решения одномерных задач распространения ударных волн в газе
Актуальной
проблемой при численном моделировании сверхзвуковых течений газа является
корректное воспроизведение скачков уплотнения. В настоящее время для расчета
таких течений широко используются методы, построенные на так называемых TVD
схемах [1, 2], использующих подход Эйлера к рассмотрению движения сжимаемой
сплошной среды. Одним из недостатков данных методов является большая численная
вязкость, приводящая к размазыванию скачков уплотнения (фронтов ударных волн).
Для решения этой проблемы Годунов [3] и др. предлагали использовать подвижные
сетки, что существенно усложняет задачу, особенно при переходе к рассмотрению
двумерных и трехмерных областей течения. В данной работе, как и в [4],
предлагается метод, использующий подход Лагранжа к рассмотрению движения
сжимаемой сплошной среды и фиксированную однородную сетку. Как будет показано
ниже на тестовых задачах, у предлагаемого метода отсутствует численная диффузия на ударных
волнах.
1. Основные положения и идея метода
Уравнения
Эйлера, описывающие одномерную задачу движения сжимаемой сплошной среды, в
размерных переменных имеют вид [1]
,
, (1)
.
Здесь 
– скорость, 
– плотность, 
– внутренняя удельная
энергия, 
– давление, 
– координата, 
– время.
Система уравнений (1) замыкается с
помощью уравнения состояния для идеального газа
, (2)
где 
– показатель
адиабаты.
Годуновым
[3] был предложен метод решения данных уравнений, заключающийся в подстановке в
явную по времени центральную конечно-разностную схему решения задачи о распаде
разрыва. В данной работе предлагается метод, использующий подход Лагранжа для
рассмотрения движения жидкости. Сначала для каждой пары ячеек решается задача о
распаде разрыва предложенным в [3] методом, в результате получаем значения
«больших» переменных: R – плотность, U –
скорость, E – внутренняя удельная энергия, P –
давление, D – скорость распространения ударной волны или волны
разрежения, - справа и слева от границы ячеек. Величины справа и слева от
границы разрыва будем обозначать индексами R и L. При этом процессы
конвекции и «акустики» рассматриваются отдельно, т.е. производится расщепление
по физическим процессам, так как местная «акустическая» скорость может в разы
отличаться от конвекционной скорости течения. Если шаг по времени для расчета
процесса конвекции оказывается меньше шага по времени для процесса «акустики»,
то конвекция не рассчитывается до первого расчёта этапа «акустики», а затем
выполняется столько расчетов этапа конвекции, сколько было пропущено.
2. Схема метода для этапа
«акустики»
На
этапе «акустики» в численном методе аналогично работе [4] рассматриваются две
волны, бегущие влево и вправо, причём левая переносит величины 
с местной
«акустической» скоростью 
, а правая - 
со скоростью 
.
Предварительно для каждой
пары ячеек i и i+1 с набором данных 
и 
решается задача о
распаде разрыва предложенным Годуновым в [3] методом, в результате получаются
значения больших переменных 
, которые записываются в ячейки сетки следующим образом
, 
, 
, 
, 
, (3)
они составляют вектор 
волны, бегущей в
отрицательном направлении оси x (влево); и
, 
, 
, 
, 
, (4)
которые, в свою очередь, составляют вектор 
волны бегущей в
положительном направлении оси x (вправо). В случае волны
разрежения переменой D присваивается скорость
более медленной характеристики волны разрежения. Например, для правой волны
разрежения
, (5)
где
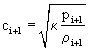. (6)
Рассмотрим волну, бегущую в положительном направлении оси x
(вправо). Ячейки рассматриваются попарно. Координаты ячеек после перемещения на
этапе акустики для «правой» волны определятся как
,
. (7)
Решения задачи на этапе «акустики» ищется в следующем виде:
1) Если выполняется условие
, (8)
тогда
1.1) если
, (9)
где 
- допуск, связанный
погрешностью машинной арифметики, то имеем «слабую» ударную волну, которая не
обгоняет решение из впереди стоящей ячейки, поэтому решение определится как
, 
, 
, 
, если 
,
, 
, 
, 
, если 
; (10)
1.2) если
, (11)
то решение определится как
, 
, 
, 
,
если 
и 
, (12)
так как имеем ударную волну, и
, 
, 
, 
,
если 
и 
, (13)
так как имеем волну разрежения.
2) Если 
, то
a) если 
, то имеем ударную волну
, 
, 
, 
, если 
,
, 
, 
, 
, если 
. (14)
b) Если 
, то имеем волну разрежения и решение для 
определяется из
условия сохранения инвариантов Римана
,
,
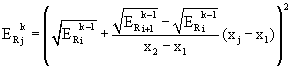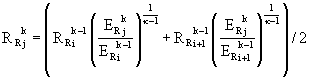, (15)
.
При выполнении условий 1) и 2), если оказывается, что в ячейку сетки на данном
подшаге уже было записано решение, то оно заменяется «новым», когда давление
«нового» решения больше давления решения уже имеющегося в ячейке сетки. Кроме
того, при записи решения в ячейки сетки также проверяется условие, чтобы
распространение данных решений с местной «акустической» скоростью не обгоняло
(не затирало) решение впереди идущей ударной волны, если таковая существует.
Для волны, бегущей в
отрицательном направлении оси x (влево) и переносящей
величины 
, условия и выражения, записанные выше, получаются
аналогичным образом.
После
перемещения левой и правой волн в каждой ячейке сетки мы имеем наборы величин 
и 
, для которых снова решается задача о распаде разрыва
предложенным в [3] методом. Причём в начальных данных задачи значения 
считаются
расположенными слева от границы разрыва, а значения 
- справа. В
результате снова получаем значения «больших» переменных 
.
Так как давление и
конвективная скорость не испытывают скачка в распаде разрыва, то их значения
после подшага «акустики» определятся как
, 
. (16)
Значения для плотности и энергии выбираются исходя из физического смысла
решения. Если 
, то выбирается решение для ударной волны. В случае если
имеем две ударные волны или пограничный случай, когда ударные волны
отсутствуют, то решение находится следующим образом
, 
, если 
или 
,
, 
, если 
или 
. (17)
Если 
, то выбирается решение для волны разрежения. В случае если
имеем две волны разряжения или пограничный случай, когда волны разряжения
отсутствуют, то решение находится следующим образом
, 
, если 
или 
,
, 
, если 
или 
. (18)
3. Схема метода для этапа конвекции
В предлагаемом методе на этапе конвекции ячейки
также рассматриваются попарно. Координаты ячеек после перемещения на этапе
конвекции определяются как
,
. (19)
Решения задачи на этапе конвекции отыскиваются в следующем виде:
1) Если выполняется условие
, (20)
то имеем ударную волну
a) если
, (21)
то решение определится как
, 
, 
, 
, если 
,
, 
, 
, 
, если 
; (22)
b) если
, (23)
то
- если 
, сначала определяется граница разрыва
, (24)
затем в ячейку j слева от границы разрыва записывается решение
, 
, 
, 
, (25)
а в ячейку j+1 справа от границы разрыва записываются величины
, 
, 
, 
, (26)
- если 
, решение определится как
, 
, 
, 
, если 
и 
,
, 
, 
, 
, если 
и 
. (27)
2) Если
, (28)
имеем волну разрежения и решение для 
определяется из
условия сохранения инвариантов Римана
,
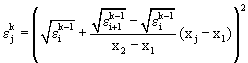, (29)
,
.
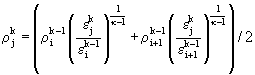При выполнении условий 1) и 2), если оказывается, что в ячейку сетки на данном
подшаге уже было записано решение, то оно заменяется «новым», когда давление
«нового» решения больше давления решения уже имеющегося в ячейке сетки.
4. Тестирование метода
Предлагаемый
метод тестировался на известной задаче, которая была в свое время предложена
Рое [1] и имеет следующие НУ:
, 
, 
, если 
,
, 
, 
, если 
. (30)
Область моделирования принималась
равной 
, сетка содержала 100 ячеек, шаг сетки составлял 
. Эти данные аналогичны параметрам моделирования задачи в
работе [2].
Шаг по времени для процесса «акустики» выбирался согласно
критерию Куранта-Фридриха-Леви
, (31)
где 
- «акустическая»
скорость распространения ударной волны; 
, т.е. ударная волна на этапе «акустики» перемещалась на одну
ячейку сетки.
Шаг по времени для процесса конвекции выбирался по
аналогичному правилу
, (32)
где 
- конвективная
скорость распространения ударной волны; 
, т.е. ударная волна на этапе конвекции перемещалась на две
ячейки сетки.
Маршевый шаг равнялся 
. Этап «акустики» выполнялся через 6 шагов по времени, т.е. 
, этап конвекции – через 10 шагов 
.
Результаты
расчетов после 110 маршевых шагов по времени показаны на рисунках 1-3 в
сравнении с точным решением Годунова [3] и данными работы Хартена [2],
полученными им для схемы ULT1C.
Графики
показывают отсутствие численной диффузии на ударных волнах, в отличие от метода
Хартена. Правда следует отметить, что из-за накопления ошибки округления
ударная волна запаздывает в показанный момент времени на одну ячейку сетки.
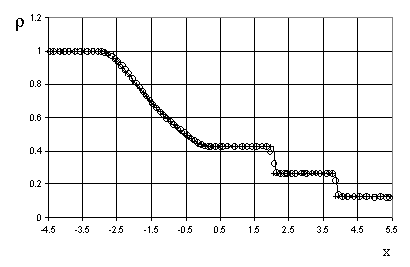
Рис. 1. Распределение
плотности в задаче о распаде разрыва (30)
- точное решение Годунова [3], 
- решение Хартена [2],
- предлагаемый метод
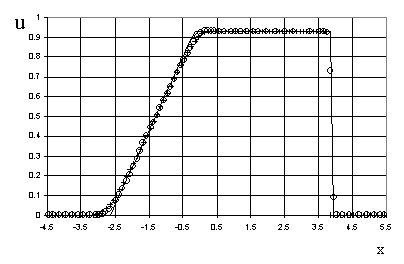
Рис. 2. Распределение
скорости в задаче о распаде разрыва (30)
- точное решение Годунова [3], 
- решение Хартена [2],
- предлагаемый метод
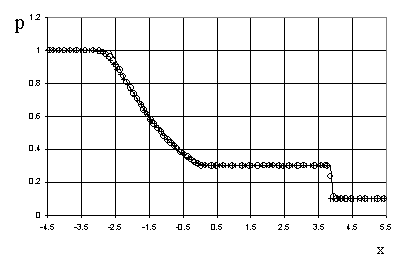
Рис. 3. Распределение
давления в задаче о распаде разрыва (30)
- точное решение Годунова [3], 
- решение Хартена [2],
- предлагаемый метод
В заключение можно сделать следующие выводы:
1) Преимуществом
предлагаемого метода по сравнению с методом Хартена является отсутствие
численной вязкости (диффузии) на ударных волнах.
2) С
течением времени ударные волны или волны разрежения могут распространяться
несколько медленнее или быстрее, чем в точном решении. Это происходит из-за
округления положения фронтов волн с точностью до ячейки сетки вследствие
применения фиксированной расчетной сетки.
Литература
1. Roe, P.L. Approximate
Riemann solvers, parameter vectors, and difference schemes // J. of Comp. Phys.
v. 135. 1997. P. 250-258.
2. Harten, A. High resolution schemes
for hyperbolic conservation laws // J. of Comp. Phys. v. 49. 1983. P.
357-393.
3. Годунов, С.К.
Численное решение многомерных задач газовой динамики / С.К. Годунов, А.В. Забродин, М.Я. Иванов,
А.Н. Крайко, Г.П. Прокопов. М.: Наука, 1976. 400 с.
4. Никонов, В.В.
Применение подхода Лагранжа к решению одномерной задачи распространения волн в
газе в рамках применимости адиабатического закона / В.В. Никонов, В.Г. Шахов //
Известия СНЦ РАН. Самара. т. 11, № 3. 2009. C. 33-37