Математика/5. Математическое моделирование

Аманбаев Т.Р., Мамешов Б.

Южно-Казахстанский государственный университет им. М. Ауэзова, Институт математики и математического моделирования КН МОН, Казахстан

О точном решении уравнения коагуляции в монодисперсной смеси при наличии источника и стока частиц

Коагуляция (слияние) частиц является одной из основных причин эволюции дисперсных систем, к которым относятся различные смеси среды (газообразной или жидкой) с частицами (твердыми или жидкими). Это явление наблюдается в различных физических ситуациях и оказывает воздействие на рост кластеров в растворах, газодисперсных системах. Подробный анализ механизмов, приводящих к движению и столкновению частиц в дисперсных системах, приведен в [1-3].

В практике часто встречаются процессы, в которых в исходном состоянии рабочая среда является однофазной, например, в виде газа (пара), а в ходе исследуемого процесса создаются условия для появления новой фазы в виде капель [4]. Именно этими процессами определяется начальная стадия фазовых переходов в однофазных (в исходном состоянии) средах (например, в переохлажденном паре). Появившиеся в результате нуклеации зародыши жидкой фазы являются достаточно мелкими и в связи с этим подвержены броуновскому блужданию. Броуновское блуждание приводит к их взаимному столкновению, поэтому является одним из основных, постоянно действующих механизмов, способствующих коагуляции микрокапель. Далее под термином “частицы” будут подразумеваться также и капли.

К настоящему времени разработано значительное число приближенных и численных методов решения кинетического уравнения парной коагуляции. Однако замкнутое аналитическое решение удается получить лишь для модельных ядер. Большое число аналитических решений с модельными ядрами приведено в монографиях [2,3], где также дана достаточно подробная библиография, посвященная этому вопросу. Заметим, что иногда (например, в случае, когда в роли частиц выступают жидкие капли) удобно записать уравнение коагуляции через объемы частиц, которое в непрерывном варианте имеет вид

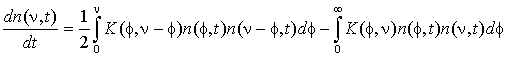(1)

Для определения общего количества частиц в единице объема необходимо проинтегрировать по всем объемам частиц

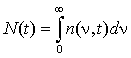
Тогда изменение общего количества частиц во времени будет равно

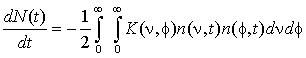(2)

В случае коагуляции монодисперсных сферических частиц ядро коагуляции примет вид . Коэффициент диффузии частиц определяется из теории броуновского движения, развитой Эйнштейном. Таким образом, ядро коагуляции в случае монодисперсных сферических частиц, подверженных броуновскому блужданию окончательно запишется в виде , где - постоянная Больцмана, T, μ – температура и вязкость несущей среды. В этом случае уравнение для общего количества частиц в дисперсной системе (2) примет более простой вид

. (3)

Если в дисперсной системе имеется постоянный или переменный источник частиц (например, из-за процесса нуклеации или конденсации) или сток частиц (например, из-за испарения, осаждения частиц на различные поверхности или гравитационной седиментации) то уравнение (3) видоизменяется и запишется в форме

, (N≥0), (4)

где - скорость появления (>0) или исчезновения (<0) частиц в единице объема смеси. Для простоты примем, что вновь появляющиеся или исчезающие из-за стока частицы того же размера, какой имеют коагулирующие частицы (это допущение справедливо, по крайней мере, в случае стока частиц или в начале процесса коагуляции при наличии источника). Уравнение для скорости изменения радиуса частиц

(5)

Из (4) следует, что при постоянном положительном значении ψ концентрация частиц с течением времени стремится к равновесному значению , причем это равновесное состояние устойчивое, поскольку

,

Уравнение (4) имеет точное решение, которое в безразмерных переменных запишется в виде

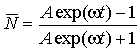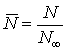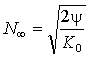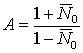, , , , (6)

где - безразмерная начальная концентрация частиц. Из (6) следует, что концентрация частиц достигает своего предельного значения =1 за бесконечное время. С учетом (6) уравнение (5) имеет следующее решение, отражающее закон изменения радиуса коагулирующих частиц (микрокапель)

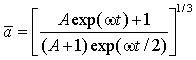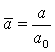, (7)

где - начальный радиус частиц.

При постоянном отрицательном значении ψ<0 (сток частиц) равновесного состояния для дисперсной системы не существует и концентрация частиц с течением времени стремится к нулю. В этом случае решением уравнения (4) будет функция

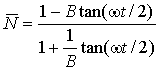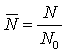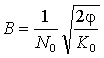, , , , φ=−ψ>0 (8)

Отсюда видно, что концентрация частиц достигает нулевого значения за конечное время . Причем с увеличением параметра B время исчезновения дисперсной фазы в системе стремится к предельному значению . Это означает, что наличие стока даже бесконечно малой интенсивности приведет к исчезновению частиц за конечное время.

При наличии стока дисперсной фазы для радиуса частиц имеем следующую формулу

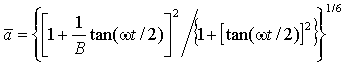(9)

Предельный радиус частиц, соответствующий моменту исчезновения t= можно рассчитать по формуле .

Ниже на рис. 1 и 2 показано примерное поведение решений (6), (7) при различных значениях начальной концентрации частиц =0 (кривая 1), 0.5 (2), 2 (3), 5 (4). Рис. 3, 4 иллюстрируют характер поведения решений (8), (9), соответствующих наличию стока частиц в дисперсной системе. Кривые 1-6 отвечают значениям параметра B=0.01; 0.05; 0.1; 0.25; 0.5; 1. На рис. 4 точки, где заканчиваются кривые, соответствуют нулевому значению концентрации частиц.

Работа выполнена при поддержке гранта (1117/ГФ2) Министерства образования и науки Республики Казахстан.

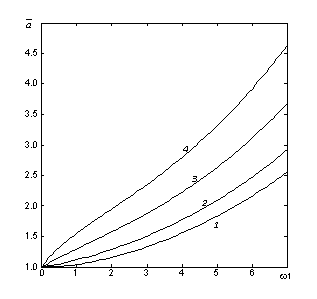
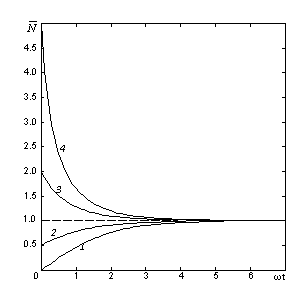
Рис.1. Рис. 2.

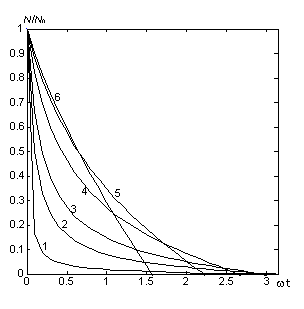
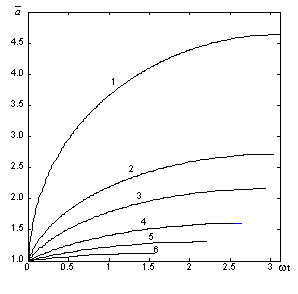
Рис. 3. Рис. 4.

Литература

1. Райст П. Аэрозоли. Введение в теорию. - М.: Мир, 1987. – 280 с.

2. Волощук В.М., Седунов Ю.С. Процессы коагуляции в дисперсных системах. – Л.: Гидрометеоиздат, 1975. – 370 с.

3. Волощук В.М. Кинетическая теория коагуляции. - Л., 1984. – 284 с.

4. Нигматулин Р.И. Динамика многофазных сред. - М.: Наука, 1987.