Явтушенко Александр
Викторович,
кандидат технических наук, доцент кафедры обработки
металлов давлением
Запорожского национального технического
университета, Украина
Оптимизационный параметрический синтез прижимного
механизма вытяжного пресса
Основная функциональная задача прижимного механизма вытяжного пресса состоит в обеспечении прижима заготовки на длительном угле поворота главного вала. В современных прессах используются рычажные многозвенные механизмы, из которых наибольшее распространение получил восьмизвенный механизм (рис.1), составленный из трех простейших механизмов [1–6]. Несмотря на его широкое применение в технической литературе практически полностью отсутствуют рекомендации по его проектированию. Основным методом синтеза подобных механизмов является графический, который при его простоте и наглядности не может обеспечить определение комбинации параметров, в наилучшей степени соответствующих назначению механизма. По этой причине создание новых конструкций прессов требует разработки метода синтеза его параметров, удовлетворяющих определенные конструктивные и технологические требования.
Создание механизма начинается с его синтеза, т. е. определения его структуры (структурный синтез) и геометрических параметров (параметрический синтез), однозначно определяющих схему механизма [7, 8]. Рычажные механизмы не могут обеспечить абсолютный выстой рабочего звена механизма (ползуна) даже на малом угле поворота главного вала, поэтому речь идет об использовании механизма, который при рабочем ходе обеспечивает отклонение ползуна ∆S от нижнего положения не более некоторой установленной величины ∆Sд. Практически на участке рабочего хода обеспечивается движение ползуна с предельным отклонением от нижнего положения не превышающим заданное значение, т. е. всегда выполняется условие
. (1)
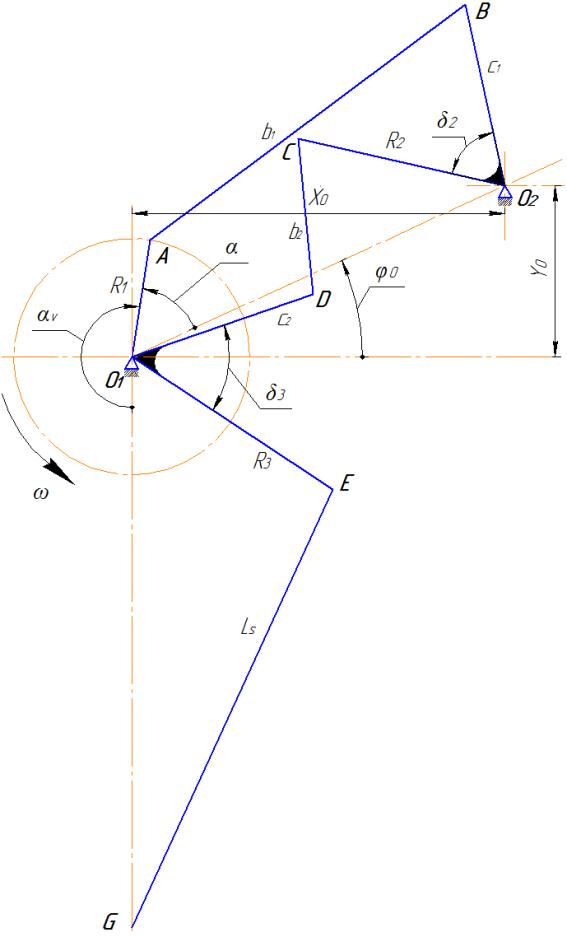
Рис. 1 – Схема прижимного механизма вытяжного пресса
Главным критерием при оценке функциональных возможностей механизма
заданной структуры принимается максимальное количество Mmax экстремумов передаточной функции 
и их положение на
интервале 
, при допустимых значениях параметров 
. Принимается, что параметры находятся в области допустимых
значений Θ, в которой обеспечивается функционирование механизма,
т. е. 
.
Для любого механизма имеется, по меньшей мере, два
экстремума функции положения, один из которых достигается в точке 
, а второй на интервале [0, 2π]. Число экстремумов Mmax
всегда четное. Присоединение механизма с одной степенью
подвижности к механизму, имеющему Mmax экстремумов,
увеличивает число Mmax образованного
механизма на 2 или 4. Функциональные возможности механизма будут тем
выше, чем больше число экстремумов Mmax, и
чем больше интервал угла поворота главного вала, на котором они имеют место.
При этом важно, что если для данной структурной схемы механизма найдено число Mmax, то всегда возможно создание
механизма этой же структуры с числом экстремумов, равным 2, 4, 6, …, Mmax–2.
На рис. 2 показан типовой график движения прижимного Sп и вытяжного Sв ползунов пресса. На
рисунке обозначено: αквп,
αкнп –
соответственно, угол крайнего верхнего и крайнего нижнего положения вытяжного
ползуна; αнп, αкп – соответственно
угол начала и конца прижима, т. е. выстоя прижимного ползуна; αс – угол выстоя
прижимного ползуна после вытяжки; Sp
– рабочий ход вытяжного ползуна. Один экстремум соответствует крайнему верхнему
положению ползуна (обозначен 10), остальные (обозначенные 2–8) расположены на рабочем участке. Если
максимальное отклонение на участке рабочего хода удовлетворяет условию (1), то
всегда существует еще две характерные точки на графике функции положения
механизма, в которых также выполняется это условие. На рис. 2 эти точки обозначены
соответственно 1 и 9, и соответствуют началу и концу процесса прижима. Таким образом,
в общем случае участок «псевдовыстоя» ползуна определяется координатами крайних
точек α1 и α9. Интервал угла
поворота ведущего кривошипа 
и есть интервал поворота,
на котором обеспечивается выполнение условия (1). Зависимости для расчета
перемещения Sп прижимного
ползуна представлены в работе [9].
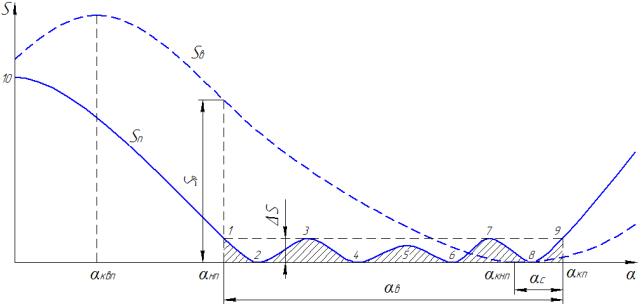
Рис. 2 – Графики движения ползунов вытяжного пресса
Задача параметрического синтеза механизма состоит в определении его геометрических параметров, обеспечивающих указанный вид функции положения и удовлетворяющих ряд условий.
Параметры механизма qi (i = 1…12) суть геометрические размеры звеньев R1, b1, c1, R2, b2, c2, R3, Ls, два угла раствора δ2 и δ3 трехплечих рычагов BO2C, DO1E, размеры, определяющие взаимное положение опор X0 и Y0. Любые из указанных параметров могут назначаться проектировщиком исходя из условий компоновки, условий необходимой прочности или жесткости и представляют собой назначаемые параметры. Если условия синтеза, имеющие форму уравнений, позволяют вычислить одни параметры через другие, такие параметры являются вычисляемыми. Все остальные параметры могут принимать любые значения в области допустимых решений, являются свободными (варьируемыми) и подлежат определению в результате синтеза. В общем случае будем все 12 параметров механизма считать свободными.
Условия синтеза делятся на главное, обязательные и желательные.
Обязательные условия синтеза обычно выражаются неравенствами и являются условиями обеспечения функционального назначения механизма и условиями существования механизма.
Механизм прижима должен обеспечить прижим заготовки при
повороте главного вала на заданном угле 
, поэтому первое обязательное условие синтеза представляет
собой неравенство
, (2)
где αвn, αвv – соответственно нижнее и верхнее допустимое значение угла αв выстоя ползуна.
Углы поворота α1 … α9 главного вала, соответствующие точкам экстремума функции положения, определяются по зависимостям, приведенным в [6].
Второе обязательное условие синтеза состоит в том, что после окончания процесса вытяжки для обеспечения выхода вытяжного пуансона из деформированной заготовки (снятия заготовки с пуансона) прижимной ползун должен оставаться неподвижным при повороте главного вала на заданный угол αс.
Возможны два варианта конструктивного исполнения механизма
прижима и механизма вытяжного ползуна. В первом варианте привод вытяжного и прижимного
ползунов производится от раздельных кривошипов, выполненных на общем валу, но
смещенных относительно друг друга на определенный угол. В таком случае крайнее
нижнее положение вытяжного ползуна αкнп
определяется геометрическими параметрами вытяжного механизма и для синтеза рассматриваемого
механизма считается известным. Во втором варианте исполнения привод обоих
механизмов производится общим кривошипом и тогда нижнее положение вытяжного
ползуна совпадает с нижним положением кривошипа О1А на рис. 1.
В практике расчетов механических прессов принято отсчет угла поворота главного
вала αv
производить от линии движения ползуна против движения вала. Из рис. 1 следует,
что углы α и αv
взаимосвязаны уравнением
, (3)
где φ0 – установочный угол центров опор (см. рис.1).
Окончание процесса деформирования происходит в крайнем
нижнем положении вытяжного ползуна при 
. Тогда из (3) следует, что угол αкнп, соответствующий крайнему нижнему положению
вытяжного ползуна равен
.
Второе условие синтеза тогда представляется в виде неравенства
, (4)
где αсn, αсv – соответственно нижнее и верхнее допустимое значение угла выстоя прижимного ползуна после окончания вытяжки заготовки.
Третье обязательное условие существования первого механизма как четырехзвенника кривошипного типа состоит в удовлетворении неравенства
, (5)
где L0 – расстояние между центрами опор, определяемое размерами X0 и Y0.
Желательные условия синтеза представляют собой ограничения, накладываемые на варьируемые параметры по конструктивным условиям и ограничения углов давления.
Все варьируемые параметры механизма могут принимать значения из указанного диапазона
, (6)
где qin, qiv – соответственно нижнее и верхнее допустимое значение i –го параметра, установленные по конструктивным условиям.
Как указано выше, желательными условиями синтеза являются также интервалы изменения углов αв и αс.
Предварительные расчеты механизма показывают, что при параметрах, удовлетворяющих условиям (6) углы давления во всех шарнирах значительно меньше допустимых, поэтому в процессе синтеза их расчет может не производиться. При необходимости, значения углов давления могут быть определены по зависимостям, приведенным в работе [10, 11].
Главное условие синтеза состоит в том, что механизм должен с заданной точностью воспроизводить заданное движение рабочего органа. В данном случае это условие состоит в том, чтобы на участке прижима удовлетворялось неравенство (1). С практической точки зрения такое условие не совсем соответствует требованиям технологического процесса. Удовлетворение условия (1) хотя бы в нескольких точках функции положения означает, что в остальных точках величина отклонения ∆S будет гораздо меньше ∆Sд. Это приведет к тому, что прижим заготовки будет осуществляться переменным усилием с амплитудой, пропорциональной величине ∆S.
Условие (1) можно ужесточить, потребовав, чтобы все
экстремумы функции положения на участке прижима были минимальными. Для этого
достаточно потребовать, чтобы среднеинтегральное отклонение величины ∆S на участке прижима было минимальным, т. е. чтобы
обеспечивался минимум интеграла Fz
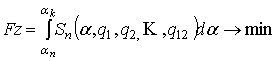. (7)
Геометрически это означает минимум площади, ограниченно осью
абсцисс и кривой функции положения на участке прижима (заштрихованная область
на рис. 2). Пределы интегрирования определяются границами участка прижима,
т. е. 
.
Таким образом, задача синтеза, состоящая в минимизации функции цели (7) при одновременном выполнении условий (1), (2), (4)–(6) представляет собой задачу нелинейной однокритериальной многопараметрической условной оптимизации. Решение таких задач возможно специальными методами, например методом деформируемого многогранника (комплексный метод Бокса), методом сопряженных градиентов и др. [12, 13].
Результаты расчетов и их сопоставление с результатами расчета механизма прижима действующего пресса усилием 8 МН показали следующее.
При исходных данных варьируемых параметров, удовлетворяющих условия (1), (2), (4)–(6), решение задачи всегда сходится к конечному результату. Задача не имеет решения, если не выполняется одно из условий, или если величина угла выстоя αв превышает значение 125…130°. Среднее время одного расчета не превышает 20…25 с.
На рис. 3 показан фрагмент графиков перемещения прижимного ползуна для реального пресса (кривая Sпб) и для пресса с оптимальными параметрами (кривая Sпо). Если для реального пресса имеют место 8 точек экстремума функции положения, то при оптимальных параметрах обеспечиваются все 10 точек экстремумов. Следует отметить, что значения отклонения ∆S в экстремальных точках 3, 5 и 7 не совпадают по величине.
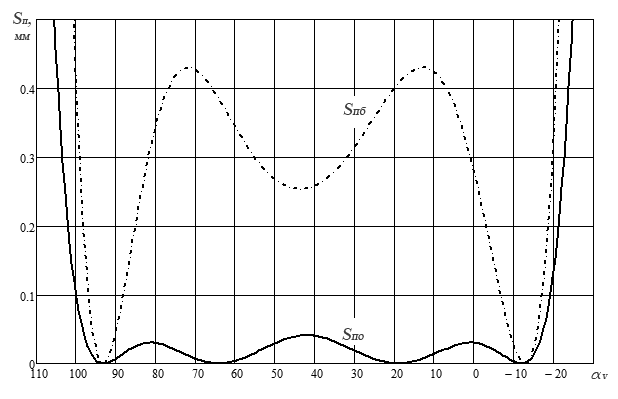
Рис. 3 – График функции положения на участке прижима
Исходные значения параметров механизма после оптимизации изменились в пределах диапазона значений, определяемых неравенствами (6). При этом значения одних параметров стали равны верхнему пределу qiv (параметры b1, b2, Ls, X0), другие – нижнему qin (параметры c2, R3, Y0). Значения остальные параметры стали равными некоторому значению внутри диапазона (qin…qiv). Однако необходимо указать, что для других вариантов исходных данных (для прессов других номинальных усилий) имеют место иные изменения начальных значений параметров, поэтому тенденции к закономерному изменению параметров не обнаружено.
Наконец, главный результат оптимизации состоит в том, что максимальная величина отклонения ползуна на заданном угле αв = 115° при оптимальном варианте параметров стала равной 0,041 мм, т. е. по отношению к реальному прессу уменьшилась примерно в 10 раз. Величина отклонения ∆S уменьшается, если ослабляются условия синтеза, например, при меньших значениях угла выстоя αв или угла αс.
Выводы
1. Представленный метод параметрического синтеза дает возможность определения оптимальных значений параметров механизма, обеспечивающих минимальную величину отклонения прижимного ползуна на участке прижима заготовки.
2. Задача условной оптимизации всегда сходится к конечному результату, если удовлетворяются все, в том числе и желательные условия синтеза.
3. Метод оптимизационного синтеза дает возможность определения параметров механизма при различных вариациях начальных параметров и условий синтеза.
4. Представленный метод полностью исключает необходимость графических построений, предварительных аналитических вычислений и обеспечивает высокую точность полученных результатов.
5. Оптимизационный параметрический синтез обеспечивает создание механизма, имеющего величину предельного отклонения прижимного ползуна не более 0,05–0,1 мм, что в несколько раз меньше, чем величина отклонения реальных вытяжных прессов.
Список использованной литературы
1. Живов Л.И., Овчинников А.Г., Складчиков Е.Н. Кузнечно-штамповочное оборудование: Учебник для вузов / Под ред. Л.И. Живова. – М.: Изд-во МГТУ, 2006. – 560 с.
2. Бочаров Ю.А. Кузнечно-штамповочное оборудование: Учебник для вузов – М.: Издательский центр «Академия», 2008. – 480 с.
3. Свистунов В.Е. Кузнечно-штамповочное оборудование. Кривошипные прессы. – М.: МГИУ, 2008. – 704 с.
4. Кривошипные кузнечно-штамповочные машины / Под ред. В.И. Власова. – М.: Машиностроение, 1982. – 424 с.
5. Ланской Е.Н., Банкетов А.Н. Элементы расчета узлов и деталей кривошипных прессов. – М.: Машиностроение, 1966. – 380 с.
6. Тынянов В.Н., Федоркевич В.Ф., Филькин И.Н. Эксплуатация кривошипных прессов двойного действия – М.: Машиностроение, 1968. – 164 с.
7. Явтушенко А.В. Задачи и методы синтеза исполнительных механизмов // Обработка металлов давлением: Сборник научных трудов. – Краматорск: ДГМА, 2014, № 1 (38). С. 245-250.
8. Явтушенко А.В. Методы и условия синтеза исполнительных механизмов механических прессов // Материалы 10-й международной научно-практической конференции «Новейшие научные достижения. – Т. 32. Технологии. – София, «Бял ГРАД-БГ» ООД. – 2014. С. 35-37.
9. Явтушенко А.В., Явтушенко А.В., Васильченко Т.А. Кинематика многозвенного прижимного механизма механических прессов // Современная техника и технологии. – Март 2014. - № 3 [Электронный ресурс]. URL:http://technology.snauka.ru/2014/03/3324 (дата обращения: 17.03.2014).
10. Явтушенко А.В. Аналитический расчет кинематических характеристик механизма прижима вытяжного пресса двойного действия // Материалы 10-й международной научно-практической конференции «Новейшие научные достижения. – Т. 32. Технологии. – Варшава, еее. – 2014. С. 35-37.
11. Левитский Н.И. Теория механизмов и машин. – М.: Наука, 1979. – 576 с.
12. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. – М.: Высш. шк., 2002. – 544 с.
13. Исследование операций / В 2-х томах. / Под ред. Дж. Моудера, С. Элмаграби. – М.: Мир, 1981. Т. 1. – 712 с.