Винник Н.І., Глоба В.С., Рябоконь Ю.О.

Національний авіаційний університет, Україна

Шифрування зображення на основі динамічних систем

Захист інформації грає важливу роль для різних типів підприємств, держави і навіть для звичайних людей, які намагаються зберегти власні дані від небажаного розголошення. Кожного дня створюються все нові алгоритми шифрування даних для забезпечення захисту конфіденційності та цілісності інформації. Також до даної сфери відноситься захист зображень та аудіо повідомлень оскільки за рахунок малюнка чи звукового запису зловмисник може скористатись інформацією, яку дістане з вказаних даних, а такий варіант розвитку подій не вигідний стороні, що хоче зберегти конфіденційність інформації.

Для сучасної криптографії характерне використання відкритих алгоритмів шифрування, що допускають використання обчислювальних засобів. Через велику поширеність DES було запропоновано багато способів підвищення його безпеки, зокрема, замінити S-блоки DES новими, які є стійкішими до лінійної атаки. Однак, широкого практичного застосування жодна з видозмінених версій DES не набула. Винятком є 3DES, однак, це не видозміна алгоритму, а лише особливий режим шифрування звичайним DES.

В програмному забезпеченні використовується технологія шифрування даних з використанням двох динамічних систем. Однією з них є динамічна система Ресслера, а другою динамічною системою – кубічним відображенням [1].

Обидві динамічні системи є чутливими до початкових умов та володіють властивістю ергодичності.

,

де змінні x, y, z – динамічні параметри системи; p, q, r – значення статичних параметрів системи. При p = 0.2, q = 0.1, r = 4.5 має місце хаотична динаміка.

Отримана при моделюванні, траєкторія кривої, що описує стан системи Ресслера у фазовому просторі та часова залежність динамічного параметра x від часу приведені на рис.1-2, відповідно.

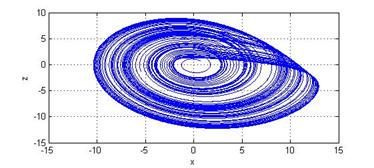
Рис. 1 - Траєкторія стану системи Ресслера в фазовому просторі

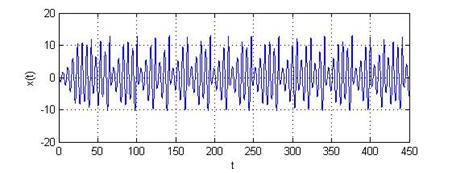
Рис. 2 - Часова залежність змінної х хаотичної системи Ресслера

Математична модель кубічного відображення має наступний вигляд:

де х – динамічна змінна, a та b – параметри системи, n = 1,2,3,… – номер ітерації.

Моделювання еволюційної поведінки цього відображення здійснювалось в програмному середовищі Matlab при різних значеннях параметрів системи a та b, що належать інтервалам [-0.6; 0.6] і [0.8; 2.5] відповідно. Отримані в процесі моделювання біфуркаційні діаграми приведені на рис.3-4. З отриманих результатів моделювання випливає, що при більших значеннях параметра b кубічне відображення демонструватиме більш розвинену хаотичну динаміку системи [2].

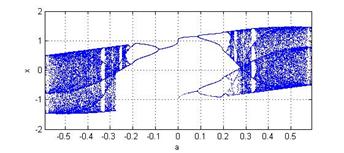
Рис. 3 - Математична модель кубічного відображення при значенні b = 2,1

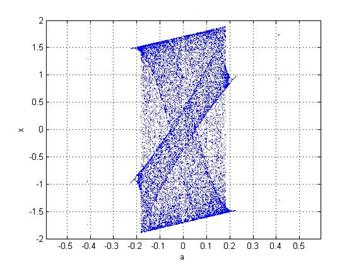
Рис. 4 - Математична модель кубічного відображення при значенні b = 2,7

Література:

1. Шахтарин Б.И., Кобылкина П.И., Сидоркина Ю.А., Кондратьэв А.В., Митин С.В. Генераторы хаотических колебаний. – Москва. – 2007. – 247 с.

2. Кузнецов А.П., Савин А.В., Тюрюкина Л.В. Введение в физику нелинейных отображений. – СПб. – 2010. – 134 с.