Шилинец В. А., Шах Е. Г.

Белорусский государственный педагогический университет

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОДНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ БИКОМПЛЕКСНЫХ ФУНКЦИЙ

В ряде работ [1–6] с помощью гиперкомплексных функций, моногенных в смысле В.С.Федорова (F-моногенных) [7], исследовались дифференциальные уравнения и системы дифференциальных уравнений в частных производных.

В данной работе с помощью F-моногенных бикомплексных функций для системы дифференциальных уравнений в частных производных

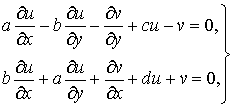(1)

где – искомые комплексные функции класса ( через обозначаем класс комплексных функций от , имеющих непрерывные частные производные первого порядка в некоторой односвязной области плоскости ), – комплексные константы, , решена следующая задача Коши.

Задача. Найти в области решение системы дифференциальных уравнений в частных производных (1), удовлетворяющее условиям

(2)

где – известные аналитические в области функции.

Исследуем сформулированную задачу Коши.

Используя следующую подстановку

, (3)

получим

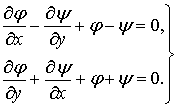(4)

Используя бикомплексные функции и формальные производные [8], легко показать, что система дифференциальных уравнений в частных производных (4) эквивалентна следующему дифференциальному уравнению в формальных производных:

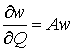, (5)

где , , , , , .

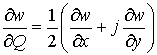Как следует из работы [1], общее решение уравнения (5) имеет вид

, (6)

где , – произвольная бикомплексная функция, F-моногенная по функции в области , .

Исследуем более подробно общее решение уравнения (5), которое задается формулой (6).

Как известно [9], бикомплексная функция , F-моногенная по функции в области , имеет вид

, (7)

где – произвольные аналитические в области функции от соответственно, , , , , .

Заметим, что

, , , .

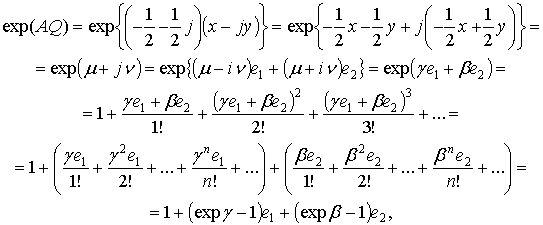
Тогда общее решение (6) дифференциального уравнения в формальных производных (5) можно записать в виде

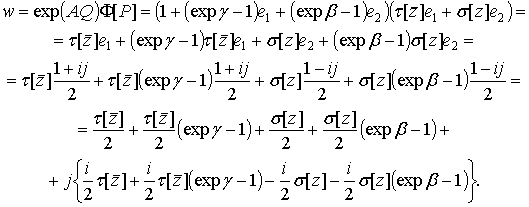
Но , следовательно общее решение системы дифференциальных уравнений в частных производных (4) примет вид

. (8)

Так как

, ,

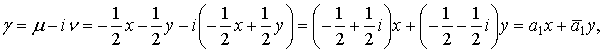
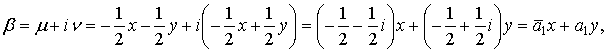
то из (8) следует

, (9)

, (10)

где – произвольные аналитические в области функции от соответственно.

Используя (3), из равенств (9) і (10) будем иметь

, (11)

. (12)

Пусть . Тогда из равенств (11) и (12) согласно условиям (2) получаем

,

.

Отсюда следует

, (13)

. (14)

Заметим, что в правых частях равенств (13), (14) имеем аналитические от в области функции. Найдя тейлоровские коэффициенты правых частей последних равенств, тем самым найдем и тейлоровские коэффициенты левых частей равенств (13) і (14).

Литература

1. Стельмашук Н.Т., Шилинец В.А. Метод формальных производных для решения задачи Коши для одной системы дифференциальных уравнений в частных производных // Дифференциальные уравнения, 1993.– Т. 29, № 11.– С. 2019-2020.

2. Стельмашук Н.Т., Шилинец В.А. Решение задачи Коши для одной системы дифференциальных уравнений методом F-моногенных функций //Весці АН Беларусі. Сер. фіз.-мат. навук,1993.–№ 3.– С.108-110.

3. Стэльмашук М.Т., Шылінец У.А. Аб рашэнні задачы Кашы для адной сістэмы дыферэнцыяльных раўнанняў у частковых вытворных метадам фармальных вытворных // Весці БДПУ,1996.– № 2.– С. 75-79.

4. Стельмашук Н.Т., Шилинец В.А. Решение краевой задачи для одной системы дифференциальных уравнений в формальных производных //Весці НАН Беларусі. Сер. фіз.-мат. навук, 1999.– № 3.– С. 127-128.

5. Стельмашук Н.Т., Шилинец В.А. О преобразовании к каноническому виду системы линейных уравнений в частных производных с помощью двойных дифференциальных операторов // Весці НАН Беларусі. Сер. фіз.-мат. навук, 2008.– №2.– С. 61-65.

6. Стэльмашук М.Т., Шылінец У.А., Трафімовіч Ю.В. Даследаванне сістэмы дыферэнцыяльных раўнанняў у частковых вытворных трэцяга парадку // Весці БДПУ. Серыя 3, 2009.– №2.– С. 8-11.

7. Федоров В.С. Основные свойства обобщенных моногенных функций // Известия вузов. Математика, 1958.– № 6.– С. 257-265.

8. Гусев В.А. Об одном обощении ареолярных производных // Bul. Stiint. si Tehnic Inst. Pol. Timisoara, 1962.– T.7, f. 2.– P. 223-238.

9. Стельмашук Н.Т. О некоторых линейных дифференциальных уравнениях в частных производных в дуальной и бикомплексной алгебрах // Известия вузов. Математика, 1964.– № 3.– С. 136-142.