Мищенчук В. В., Юзькова В. Д.

Буковинский государственный медицинский университет, Украина

Черновицкий областной институт последипломного педагогического образования

Импедансная спектроскопия одностадийной электродной реакции на вращающимся дисковом электроде

В наше время метод импедансной спектроскопии находит все большее использование вследствие своей высокой информативности и обеспечении исследователя приборами высокой точности и чувствительности [1].

Импеданс электрохимических систем рассматривается как комплексная величина, которая служит для определения констант скоростей окислительно-восстановительных реакций или адсорбционных процессов, емкости двойного электрического слоя, омического сопротивления (электропроводности, коэффициентов диффузии) и т.д.

Из-за того, что метод импедансной спектроскопии чувствителен к механизмам переноса заряда необходимо знание количественной модели всех процессов переноса заряда в электрохимической системе, что даст возможность в полной мере использовать потенциал этого метода.

В литературе описан только импеданс систем с учетом диффузии и конвекции, в то же время миграция электроактивных компонентов, игнорируется.

В работе построена математическая модель, которая может описывать кинетику одностадийного процесса с учетом миграции, диффузии и конвекции электроактивных компонентов на вращающимся дисковом электроде. Модель получена интегрированием уравнений массопереноса в допущении линейности концентрационного профиля и может количественно описывать процесс при небольших значениях перенапряжения. На основе модельных уравнений рассчитывается электрохимический импеданс, который в свою очередь может быть использован в методе импедансной спектроскопии с целью определения кинетических параметров реакции.

Рассматривается одностадийный электродный процесс:

Выражения для скоростей электродных процессов:

,

,

- концентрации возле поверхности электрода электроактивных частиц – окисленной и восстановленной формы соответственно.

Для вращающегося дискового электрода в растворе с поверхностно-неактивным электролитом, кроме двух вышеуказанных видов ионов содержится индифферентный ион концентрации c_3, имеют место следующие одномерные изотермические уравнения многокомпонентной диффузии [2]:

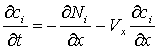, i=1...,2, 0≤x≤L, (1.1)

которые дополнены начальными и граничными условиями:

, , , i=1,…,2, (1.2)

, (1.3)

Концентрация индифферентного иона находится из условия электронейтральности:

, (1.4)

Проинтегрировав уравнения материального баланса и потоков всех компонентов по х в границах диффузионного слоя, допуская линейное распределение концентраций и используя граничные условия (1.2)-(1.3), получено следующую систему обыкновенных дифференциальных уравнений, которые описывают баланс массы с учетом транспортных процессов:

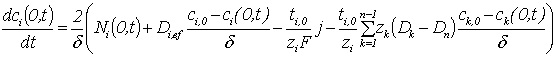, (2.2)

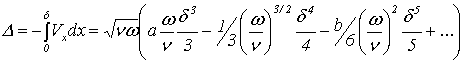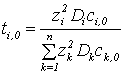где i=1,…,2; - эффективный коэффициент диффузии і-го компонента, который учитывает молекулярную диффузию в движущейся среде; - поправка на конвекцию; , - коэффициент переноса і-го компонента в объеме раствора.

В электрохимии метод импедансной спектроскопии используют разные режимы контроля электрохимической ячейки. Уравнение, которое отображает режим потенциостатического контроля трех/двухэлектродной ячейки (рис.1):

R_s S∙j(t)+E(t)=U=const , (2.3)

R_s – омическое сопротивление, S – площадь рабочего электрода, U – фиксированное значение ЭРС между потенциализмеряющими электродами (Comp и Ref) потенциостата / импедансометра.

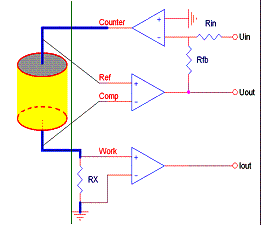
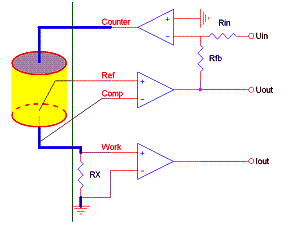
Рис 1. Способы подключения (контроля ячейки) потенциостатом / импедансометром: а) – двухэлектродное подключение; б) трехэлектродное подключение.

Литература

1. E. Barsoukov, J. Ross Macdonald, Impedance Spectroscopy Theory, Experiment, and Applications. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. 2005, P. 606.

2. J. S. Newman, Electrochemical Systems, Prentice-Hall, Inc. Englewood Cliffs, New Jersey, 1973, P. 464.