Математика/4. Прикладная математика
К.ф.-м.н.
Зинченко А.Б., Павлов А.Е.
Южный
федеральный университет. Россия
NS-ядро кооперативной
игры с трансферабельной
полезностью
В кооперативной игре с
трансферабельной полезностью (ТП-игре) 
, где
, 
, 
, 
,
предполагается, что сформировалась коалиция всех
участников. Решения игры 
предлагают способы
распределения веса 
максимальной коалиции
с учетом возможностей других коалиций 
. Одно из важнейших направлений в теории кооперативных игр
связано с содержательной интерпретацией решений, описанием их сходства и
отличия, а также рекомендациями по выбору концепции решения для специальных
классов игр.
Основным решением-множеством кооперативной
игры является С-ядро (core) [1]
,
где 
- множество
дележей. При дележах из С-ядра каждая
собственная коалиция 
получает не меньше,
чем может достичь самостоятельно. Среди одноэлементных решений (значений игры)
наиболее популярны: N-ядро (nucleolus) [2],
обозначаемое через 
, и значение Шепли (Shapley
value) [3], обозначаемое через 
.
В данной работе вводится новое
одноточечное решение ТП-игры, балансирующее две, в некотором смысле,
противоположные концепции решения 
и 
. Новое решение, названное NS-ядром и обозначенное через 
, есть среднее арифметическое N-ядра и значения Шепли
.
N-ядро лексикографически минимизирует
вектор упорядоченных по не возрастанию эксцессов коалиций
,
где 
- вектор эксцессов 
коалиций 
, 
, 
, относительно дележа 
, 
,
- множество векторов эксцессов дележей игры 
. Положительный эксцесс отражает степень неудовлетворенности
коалиции 
дележом 
, следовательно, концепция N-ядра определена так, чтобы
сделать «самую несчастную коалицию как можно более счастливой». Выигрыши существенных
агентов в N-ядре слабо отражают их продуктивность.
Согласно значению Шепли выигрыш каждого
игрока равен его среднему вкладу во все коалиции
, 
,
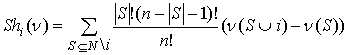т.е. выигрыш
игрока зависит только от его продуктивности.
N-ядро является селектором С-ядра сбалансированной
ТП-игры (достоинство) и всегда принадлежит множеству дележей игры общего вида
(достоинство), но не удовлетворяет аксиоме аддитивности (недостаток) и даже
ослабленной аксиоме коалиционной монотонности (недостаток). Последние свойство
очень непривлекательно, т.к. при увеличении общей прибыли 
только одной коалиции
, 
, личные выигрыши некоторых
игроков из 
могут стать меньше.
Значение Шепли - одно из немногих аддитивных и одновременно коалиционно
монотонных одноточечных решений ТП-игры (достоинство). Но оно может не
принадлежать не только С-ядру сбалансированной игры, но даже множеству дележей
(недостаток). Известно, что не существует коалиционно монотонного значения
ТП-игры, которое всегда принадлежит С-ядру сбалансированной игры. Поэтому
представляет интерес поведение NS–ядра на
всем множестве ТП-игр и на специальных классах.
Оба решения, определяющие NS-ядро, можно
интерпретировать как эгалитарные, но N-ядро реализует эгалитаризм для коалиций,
а значение Шепли – эгалитаризм для участников игры. Таким образом, новое
решение 
можно считать
компромиссным. Для кооперативной ТП-игры уже предложено несколько решений
компромиссного типа.
Консенсус-значение [4] является средним
арифметическим значения Шепли и равномерного распределения дополнительного
дохода от кооперации
, 
, 
, 
.
Консенсус-значение балансирует два крайних принципа
формирования выигрыша нулевого игрока. Игрок 
нулевой в 
, если 
, 
. Выигрыш нулевого игрока 
в значении
Шепли равен нулю 
. При равномерном распределении 
все игроки, в том числе и нулевой, получают одинаковую
долю 
дополнительного дохода от кооперации (уравниловка). В
консенсус-значении нулевой игрок может получить положительный выигрыш, но нет
уравниловки.
Существует также решение, названное 
-значением [5]
, 
, 
,
которое реализует компромисс между верхним вектором
, 
,
и нижним вектором
, 
,
компромиссно допустимой игры, т.е. игры,
удовлетворяющей условию
, 
.
Компоненты нижнего вектора – минимально возможные
выигрыши агентов для дележей, принадлежащих С-ядру, а компоненты верхнего
вектора – максимально возможные в С-ядре выигрыши агентов.
Менее известным, чем упомянутые выше,
компромиссным значением игры 
является (не имеющее
специального названия) решение
,
где 
- фиксированный
игрок, 
- вершина множества дележей, определенная формулой
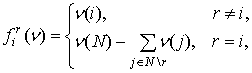
- вершина множества двойственных дележей
,
определенная формулой
В 
выигрыши всех
агентов, кроме 
-го, равны минимально возможным в множестве дележей
величинам, а 
-й игрок получает остаток распределяемой полезности 
. В 
выигрыши всех
агентов, кроме 
-го, равны максимально возможным в множестве двойственных
дележей величинам, а 
-й игрок получает остаток 
.
В
таблице 1 сравниваются свойства значения Шепли, N-ядра и NS-ядра. Используются
следующие обозначения:
·
(E)
эффективность (efficiency),
·
(A) аддитивность (additivity),
·
(Sym) симметричность (symmetry),
·
(NP) свойство нулевого игрока (null player property),
·
(ISE) инвариантность относительно
преобразования стратегической эквивалентности (invariant w.r.t. strategic equivalence),
·
(CM) коалиционная монотонность (coalition monotonicity),
·
(ACM) ослабленная коалиционная монотонность (aggregate coalition monotonicity),
·
(CS) селектор С-ядра
(core selector),
·
(IR) индивидуальная
рациональность (individual rationality).
Таблица
1
Свойства решений
|
|
E |
A |
Sym |
NP |
ISE |
CM |
ACM |
СS |
IR |
|
Значение Шепли |
да |
да |
да |
да |
да |
нет |
да |
да |
нет |
|
|
да |
нет |
да |
да |
да |
да |
нет |
нет |
да |
|
|
да |
нет |
да |
да |
да |
нет |
нет |
нет |
нет |
-ядро
-ядро
Основная трудность нахождения NS-ядра связана с вычислением N-ядра, т.к. для ТП-игры общего вида это наиболее
трудно вычисляемое решение. Нужно решить серию задач линейного программирования
с (�� + 1) переменными и 
ограничениями. В
наихудшем случае количество таких задач равно 
. Или решить одну, но очень большую задачу линейного
программирования. В обоих случаях возможен сильный «разброс» коэффициентов
симплекс таблиц, а также плохая обусловленность систем ограничений.
Для нахождения N-ядра был выбран первый способ. Создана библиотека CooperativeGames.dll, вычисляющая
значение Шепли, N-ядро и NS-ядро (C#, Microsoft Visual Studio 2015 с дополнительными
пакетами Microsoft Solver Foundation 3.1, MathNet.Numerics). Для решения задач
линейного программирования была использована библиотека Microsoft Solver Foundation Express Edition
версии 3.1. Разработано два приложения.
Первое (Windows – приложение) имеет удобный интерфейс. С помощью
этого приложения были вычислены NS-ядра
представителей классов эквивалентности крайних точек многогранника
(0,1)-нормализованных 1-выпуклых игр [6] четырех лиц (игры 
из таблиц 2 и 3).
Экстремальные игры были получены с помощью формул, выведенных в [7]. Известно,
что экстремальность игры соответствует, в некотором смысле, экстремальному
поведению участников моделируемой ситуации. Кроме того, были вычислены NS-ядра для сумм некоторых экстремальных игр (последние
три строки таблиц 2 и 3).
Таблица 2
1-выпуклые игры
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение
таблицы 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения Шепли, а, следовательно, и NS-ядра игр 
, 
, 
принадлежат С-ядру.
Значения Шепли и NS-ядра игр 
- 
, 
С-ядру не
принадлежат. Однако в игре 
значение Шепли не
принадлежит С-ядру, а NS-ядро –
принадлежит.
Таблица 3
Решения 1-выпуклых игр
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе приложение (консольное)
предназначено для тестирования программы на генерируемых данных. Игры
генерировались с помощью псевдослучайных чисел, но при условии, чтобы множество
дележей было непустым. Тестирования дало впечатляющие результаты (см. таблицу
4), за которые нужно благодарить разработчиков библиотеки Microsoft Solver Foundation Express Edition.
В частности, для решения серии задач линейного программирования с 12
переменными и 4096 ограничениями (в исходной задаче) требуется в среднем 9.3 секунды. При
вычислении NS-ядра игры 13 лиц и более,
возникает ошибка, связанная c ограничением
лицензии на библиотеку Microsoft Solver Foundation Express Edition.
Аналогично обобщенному консенсус-значению
, 
,
можно ввести обобщенное NS-ядро – выпуклую комбинацию значения Шепли и N-ядра
, 
.
Значение 
можно выбрать так,
чтобы обобщенное NS-ядро принадлежало: множеству дележей,
если значение Шепли ему не принадлежит; C-ядру сбалансированной игры, если значение Шепли ему
не принадлежит.
Таблица 4
Среднее
время вычисления NS-ядра
|
Число игроков |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Время |
45 мс |
55 мс |
91 мс |
110
мс |
287
мс |
708
мс |
1.3 с |
4.5 с |
9.3 с |
Литература:
1.
Gillies D. B. Solutions to general non-zero-sum games. In A. W.
Tucker and R. D. Luce (eds.): Contributions to the Theory of Games IV.
Princeton University Press. 1959. P. 47-85.
2. Schmeidler D. The nucleolus of a
characteristic function game // SIAM J.
Appl. Marh. 1969. V.17. P. 1163-l170.
3.
Shapley L.S. A value for
n-person games // Annals of
Mathematics Studies. 1953. V. 28. P. 307–317.
4. Ju Y., Born P., Rays P. The
consensus value: a new solution concept for cooperative games // Social Choice
and Welfare. 2006. V. 28. №. 4. P. 85-703.
5. Tijs S. Bounds for the core and the τ -value. In: O. Moeschlin and D. Pallaschke (Eds.).
Game theory and mathematical economics. 1981, pp. 123–132.
6.
Driesse T.S.H. Properties of
1-convex n-person games // OR Spektrum. 1985. №7. P. 19–26.
7. Зинченко А.Б. Многогранники специальных классов сбалансированных
игр с трансферабельной полезностью // Дискретный
анализ и исследование операций. 2016. Т.
23, № 1. C. 80–95.