ктн, доцент Василенко В. С.

Національний авіаційний університет, Україна

Модель підвищення пропускної спроможності каналів обчислювальних мереж. Рівняння частотно – енергетичного балансу

 

Забезпечення доступності та цілісності інформації, яка циркулює в цих системах є однією із основних задач технічного захисту в розподілених обчислювальних мережах (РОМ). Для телекомунікаційних систем, як елементів РОМ, ця задача трансформується в забезпечення їх високої пропускної спроможності при відсутності будь-яких модифікацій (викривлень), які не були санкціоновані її власником, не залежно від причин або джерел виникнення таких викривлень.

В [1] визначено, що при прямому (безпосередньому) розширенні смуги пропускання межа пропускної спроможності в разі, коли смуга пропускання каналу, а отже  і швидкість посимвольної передачі інформації збільшуються необмежено, дорівнює:

                            (1)

Звернемо увагу на те, що після множення правої частини цього виразу на величину , вираз (1) можна представити у вигляді [2]:

,

де:  –  швидкість посимвольної передачі інформації в каналі, при якій зафіксоване співвідношення  сигнал/завада дорівнює , а .

Підкреслимо, що спосіб розширення смуги пропускання при збільшенні швидкості посимвольної передачі інформації є найпростішим. Більш детальний аналіз показує, що у міру збільшення швидкості посимвольної передачі інформації (чи смуги пропускання ΔF каналу) його пропускна спроможність швидко зростає доти, поки середні потужності шуму і сигналу не порівняються [1]. Потім вона зростає поволі, асимптотично наближаючись до визначеного вище значення . При цьому ефективне використання смуги пропускання каналу забезпечується при , чи при  та .

Звернемо наразі увагу на те, що співвідношення сигнал/шум при максимальній швидкості посимвольного обміну дорівнює одиниці, . Зрозуміло, підвищувати надалі швидкість посимвольного обміну (та, разом із цим і пропускну спроможність каналу), використовуючи при цьому можливості багаторівневих сигналів неможливо. Дійсно, при такому співвідношенні сигнал/завада у виразі для розрахунку пропускної спроможності (1) другий множник дорівнює одиниці:  і цей вираз трансформується до вигляду:

 (біт/с).

При цьому принципово важливим недоліком цього кроку є якраз те, що  і, при цьому, величина ймовірності викривлення символу є досить великою (наприклад, при умові амплітудної модуляції є не меншою ніж ). В той же час відомо, що наприклад, згідно стандарту МККТТ (міжнародна назва тієї ж організації – ITU-T), для цифрових даних повинна виконуватися умова Рвикр < 10-6 (в окремих випадках для критичних даних цей поріг зменшують до 10-9). Отже, виходячи із умови забезпечення цілісності інформаційних символів (відсутності викривлень), при інформаційному обміні із застосуванням прямого розширення смуги пропускання повинно існувати певне обмеження такого розширення.

Тоді зрозуміло, що межа збільшення смуги пропускання повинна визначатися тією шириною смуги пропускання, при якій зберігаються вимоги діючих стандартів щодо забезпечення відсутності викривлень (забезпечення цілісності) інформаційних повідомлень. Для її визначення врахуємо, що:

Рвикр  = 0,5 ехр (− α2 h2/2),

де: α2 – коефіцієнт, який визначається видом модуляції. Виходячи із цього виразу, допустиме співвідношення сигнал/завада може бути визначеним таким, що при допустимому значенні імовірності викривлень  дорівнює . Отже, можна записати:

 

Звідси допустима ширина смуги пропускання каналу  дорівнює:

                            (2)

Оскільки  то:

          .                     (3)

Рівняння (2), (3) слід вважати рівняннями частотно – енергетичного балансу (ЧЕБ)  каналу. Дійсно із цих виразів витікає, що збільшення одного із цих параметрів, наприклад швидкості посимвольної передачі чи смуги пропускання каналу потребує відповідного збільшення потужності сигналу (при існуючому рівні  спектральної щільності потужності завади) чи зменшення спектральної щільності потужності завади (при існуючому рівні сигналу). Окрім того, із першого рівняння ЧЕБ (вираз 2) при трьох існуючих чи заданих параметрах (наприклад, потужності сигналу , спектральній щільності потужності завади ) і потрібній імовірності викривлення символу  із (2) однозначно визначається четвертий – допустима смуга пропускання . Аналогічно, із (3) при трьох існуючих чи заданих параметрах (наприклад, потужності сигналу , спектральній щільності потужності завади ) і  потрібній смузі пропускання  чи потрібному співвідношенні сигнал/ завада  однозначно визначається четвертий – допустимі співвідношенні сигнал/ завада  чи допустима смуга пропускання . Точно так же при заданих смузі пропускання  і співвідношенні сигнал/ завада  однозначно визначається потрібне співвідношення .

Із другого рівняння ЧЕБ (вираз 3) витікає також, що при сталій енергетиці каналу можна збільшувати смугу пропускання при відповідному зменшенні співвідношення сигнал/завада чи навпаки, отже існує можливість варіації цими параметрами каналу.

Звернемо увагу на те, що перше рівняння ЧЕБ (вираз 2) із використанням співвідношень (1) та (2) набуває вигляду, який можна розглядати як трете рівняння ЧЕБ:

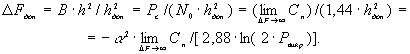     (4)

Із третього рівняння ЧЕБ (4) витікає, що заданих виду модуляції () та межі пропускної спроможності  допустима смуга пропускання каналу  визначається вимогами щодо цілісності інформаційних об’єктів (потрібною імовірністю викривлення символу) .

Врахуємо при цьому, що оскільки ширина смуги пропускання, яка розрахована згідно із (4), отримана при умові забезпечення необхідної імовірності викривлення бінарного символу, то використання інших методів збільшення пропускної спроможності каналу (наприклад, за рахунок застосування багаторівневих сигналів) є неможливим, а отже можливості прямого розширення смуги пропускання каналу є вичерпаними.

Таким чином, для заданих умов пропускна спроможність каналу може бути обрахованою, виходячи із виразу:

 біт/с,

причому допустиме значення швидкості посимвольного обміну:

.

 

1. Алишев Я. В. Предельная пропускная способность и потенциальная помехоустойчивость оптических сетей и систем телекоммуникаций. // Доклады БГУИР. 2004. – Т. 2, № 2. – С. 43-45.

2. Василенко В. С. Модель підвищення пропускної спроможності каналів обчислювальних мереж. Пряме розширення смуги пропускання каналів. //Матеріали  V міжнародної Науково – практичної конференції “ZPRÁVY VĚDECKÉ IDEJE – 2009” 07–15 жовтня 2009. INFLAČNI BEZPENOST. – Praha: “Publishing House” ”Edication and Science” s.r.o. 2009. –Т. 12, С. 49–51