Современные информационные технологии/1.Компьютерная  инженерия

Котлярова И.А.

Восточно-Казахстанский государственный технический университет имени Д. Серикбаева

Использование среды Matlab в архитектуре информационно-аналитической системы планирования доходов бюджета

В рамках бюджетного планирования очень важной задачей является прогноз ожидаемых налоговых поступлений как основного источника доходной базы с учетом особенностей социально-экономической ситуации.

Одним из подходов к решению проблемы является использование нечетких моделей [1], применение которых эффективно, когда:

- имеется недостаточность или неопределенность знаний об исследуемой системе или процессе;

- получение требуемой информации сопряжено с различными трудностями или вообще невозможно;

- основная часть информации получена на основе экспертных данных или эмпирических описаний процессов;

- параметры и входные данные не являются точными и корректно представленными.

В ходе исследования предметной области было выявлено, что значительную часть доходов бюджета Восточно-Казахстанской области составляют налоговые поступления, в большей степени индивидуальный подоходный и социальный налоги. Основываясь на методике прогнозирования поступлений бюджета [2], были выделены факторы социально-экономического развития, влияющие на данные налоговые поступления.

Для решения задачи прогнозирования доходов бюджета были разработаны три нечётких модели:

- нечёткая модель определения прироста индивидуального подоходного налога (НМИПН);

- нечёткая модель определения прироста социального налога (НМСН);

- нечёткая модель определения прироста собственных доходов бюджета области (НМСДБО).

Входными переменными для модели НМИПН являются: прирост среднемесячной заработной платы, уровень безработицы, прирост минимального расчётного показателя, выходной переменной является прирост индивидуально подоходного налога.

Для модели НМСН входными переменным являются: прирост расходов на конечное потребление, уровень безработицы, прирост внутреннего регионально продукта, выходной переменной является прирост социального налога.

Нечёткие продукционные модели образуют иерархическую структуру. Выходные переменные «Прирост ИПН» и «Прирост СН» используются в качестве входных переменных для нечёткой модели «НМСДБО».

Для каждой переменной были определены свои терм-множества и функции принадлежности. Например, для входной переменной «прирост среднемесячной заработной платы» определена лингвистическая переменная (β1) - «прирост СЗП», которая имеет следующее терм множество: T1={«очень низкий», «низкий», «средний», «высокий», «очень высокий»}.

Для построения нечётких моделей и разработки базы продукционных правил использовался FIS редактор пакета Fuzzy Logic Toolbox, входящий в состав программного средства MATLAB [3,4].

Выполнение нечеткого вывода реализовано на основе алгоритма Мамдани (Mamdani).

На рисунке 1 приведена поверхность нечеткой модели «НМИПН» для базы правил, построенная в среде MATLAB.

Данная поверхность отражает изменение прироста индивидуального подоходного налога в зависимости от прироста среднемесячной заработной платы и прироста минимального расчётного показателя. При приросте среднемесячной заработной платы на 10%, уровне безработицы 5% и приросте минимального расчётного показателя на 4%, прирост индивидуального подоходного налога составит 5,84%. Формируя всевозможные наборы данных, можно проследить, какие из правил участвуют в процессе нечёткого вывода, и, при необходимости, произвести их корректировку.

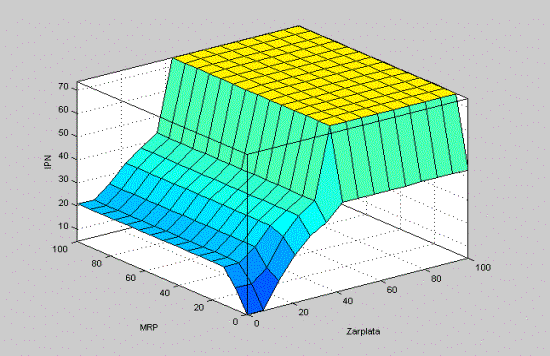
Рисунок 1 - Поверхность нечёткой модели «НМИПН» для базы правил

Разработанные продукционные модели включены в состав математического обеспечения информационно-аналитической системы планирования доходов бюджета.

Литература:

1. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближённых решений. – М.:Мир, 1976.

2. «Методика прогнозирования поступлений бюджета», Утверждена приказом Министра экономики и бюджетного планирования Республики Казахстан от 29 декабря 2008 г. №271.

3. Леоненков А.В. Нечёткое моделирование в среде MATLAB и fuzzyTECH.- СПб.: БХВ-Петербург, 2005 г. – 736 с.

4. Штовба С.Д. Проектирование нечётких систем средствами MATLAB. – М.:Горячая линия – Телеком, 2007.- 288с.