СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ / Компьютерная  инженерия.

к.т.н. Чёрный С.Г., к.т.н. Голиков С.П.

Керченский государственный морской технологический университет

Проектирование фраггмента модели мультиагентирования для GIS приложений

Основной проблемой широко распространённых технологий глобальных компьютерных сетей является невозможность универсально и эффективно использовать удалённые вычислительные ресурсы. Для преодоления ограничений и недоработок существующих решений была предложена новая технология, получившая название GRID. Технологические требования, предъявляемые к GRID чаще всего определяются как: client-server, peer-to-peer; чёткий высокоуровневый контроль над использованием ресурсов; многоуровневый контроль прав доступа, локальные и глобальные политики доступа; поддержка распределения различных ресурсов - программ, данных, устройств, вычислительных мощностей; поддержка различных моделей пользования - многопользовательской, однопользовательской, режимов performance-sensitive и cost-sensitive; контроль над качеством предоставляемых услуг, планирование, резервное предоставление услуг.

Системы поддержки рабочих процессов имеют высокую стоимость покупки и настройки, а также не затрагивают наиболее важный момент в работе анализа потоковых данных геогрупп - содержательный анализ информации для принятия решений. Технологии поддержки эвристической деятельности имеют большую трудоемкость построения и сопровождения, нацелены на решение узкоспециализированных задач, требуют наличия определенного уровня квалификации у пользователя и значительных затрат времени на работу с системой. Устранение недостатка дороговизны существующих технологий и «облегчить» систему, обеспечивающую весь цикл принятия решения возможно с использованием мультиагентного подхода, который достаточно стремительно развивается в последнее время в области создания информационных систем.

К аспектам применения мультиагентных систем можно отнести: сложность современных систем и организаций, которая достигает такого уровня, что централизованное управление в них становится неэффективным из-за наличия огромных потоков информации, когда слишком много времени тратится на ее передачу в центр и принятие им решений; компьютерные системы на сегодняшний день становятся сложнее и содержат ряд подсистем различной природы, обладающих различными функциональными характеристиками и взаимодействующих с различными специалистами, удаленными друг от друга (с ростом сложности падает надежность систем, и все труднее сформулировать их адекватную целевую функцию); решаемые задачи или разрабатываемые системы подчас неоднородны и распределены• в пространстве и в функциональном плане, поскольку ни один человек не может создать современную сложную систему в одиночку; понятие открытой системы означает, что у нее имеются развитые возможности и средства адаптации к изменениям среды, в том числе путем модификации своей структуры и параметров. При визуализации характерных данных для анализа и поддержки принятия решений, необходимо отметить особенности применения и взаимодействия систем. В теории и практике ГИС применяются пространственные прямоугольные, криволинейные, плоские прямоугольные и полярные системы координат (рис. 1). В произвольной точке эллипсоида Q() проведем нормаль QO' к этой поверхности (рис. 1), через которую можно провести бесчисленное множество нормальных сечений. Из них мы выберем два главных: сечение, совпадающее с плоскостью меридиана PQP', называемое меридианным, и сечение, ортогональное первому в точке Q, называемое сечением первого вертикала. С учётом этого определяют и используют различные системы координат: геодезическую, геоцентрическую, топоцентрическую, сфероидическую (сферическую), изометрическую и локальные системы.

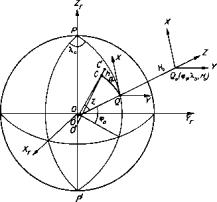
Рис. 1. Топоцентрическая горизонтная и сфероидическая (сферическая) полярные системы координат

Связь геоцентрической и геодезической системы координат выражается формулами: X_г =; Y_г = ; Z_г = ; где N = - радиус кривизны сечения первого вертикала в данной точке; , - соответственно большая полуось эллипсоида вращения и квадрат первого его эксцентриситета. Формулы связи топоцентрической и геодезической систем координат имеют вид:

;

;

,

где - соответственно географические координаты в текущих точках и точке полюса; Н₀ - высота точки полюса относительно поверхности эллипсоида; h - превышения точек.

Классификация проекции по ориентировке картографической сетки зависит от широты точки полюса Q используемой системы координат. При полюс принятой системы совпадает с географическим полюсом - получаем прямые проекции, в которых сетка меридианов и параллелей , имеет наиболее простой вид; её называют нормальной. При - получаем поперечные проекции, при - косые. В косых и поперечных проекциях нормальная сетка совпадает с сеткой вертикалов и альмукантаратов, а линии меридианов и параллелей изображаются кривыми.