Рашевський М.О.

Криворізький технічний університет

АСИМПТОТИЧНЕ ІНТЕГРУВАННЯ ДИФЕРЕНЦІАЛЬНОГО РІВНЯННЯ ДРУГОГО ПОРЯДКУ ІЗ ЗМІННИМ ЗАПІЗНЕННЯМ

 

        Питання про асимптотичне інтегрування рівняння вигляду

                           (1)

досліджене у різних припущеннях про коефіцієнти a(t, e), b(t, e) та d(t, e) [2, 4]. Тут x(t, e) – невідома функція, D(t) ³ 0 – відхилення аргументу. Мають місце зображення збіжними рядами за степенями дійсного малого параметра e > 0:

.

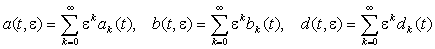У зв’язку із розв’язанням прикладних задач рівняння з відхиленням аргументу (ВА) неодноразово досліджувались при різних припущеннях про коефіцієнти. Дослідження стосувалися рівнянь із стабільним спектром граничного оператора [1]. Записане рівняння вивчалося у роботах [2, 4]. У першій із них при виконанні на проміжку [0, L] нерівності t – D(t) ³ 0 розв’язано задачу Коші

                                              (2)

У роботі [4] побудовано асимптотика частинного розв'язку, що відповідає одному з коренів характеристичного квазіполінома. Дане дослідження є розвиненням робіт [2, 4] для інтегрування рівняння (1) із нестабільним спектром у розумінні [1]. При цьому використовуються методи [1, 3, 5], розроблені для звичайних диференціальних рівнянь. Вимагатимемо виконання наступної умови.

10. Коефіцієнти ak(t), bk(t) та dk(t) є нескінченно диференційовними на проміжку [0, L], L < ¥, k ³ 0.

20. Корені рівняння  є різними для t Î (0, L] і .

Нехай також на [0, L] справджуються умови

t – D(t) ³ 0 та d0(0) = 0.                                                         (3)

При подібному обмеженні рівняння (1) досліджене у роботі [2]. Там вимагалося, щоб d0(t) º 0, тобто наявності малого параметра при доданку, що містить ВА.

          Формальний розв’язок задачі (1), (2) будуватимемо у вигляді

                                                        (4)

Підставивши (4) в (1) та прирівнявши коефіцієнти при степенях e, з урахуванням (3) дістанемо систему рівнянь

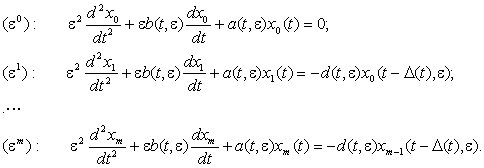
Загальний розв’язок рівняння (e0) згідно із [3] запишеться у вигляді

де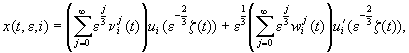

Зокрема, у випадку a(0, 0) = tp(t), p(0) ¹ 0 і b(t, 0) º 0 матимемо:

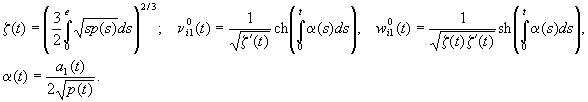
Тут ui(t) – функції Ейрі [1, 3], i = 1, 2. Довільні сталі визначимо так:  Розв'язок наступного рівняння (e1) запишеться у вигляді

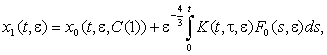
де Набір сталих C(1) визначимо так, щоб . Згідно із [1, 3] внаслідок виконання другої з умов (3) справджується оцінка 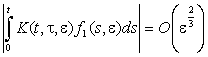. Описаним способом визначаємо інші доданки суми (4):

.

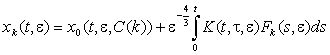Набір сталих C(k) визначимо так, щоб , k £ m. Таким чином отримуємо формальний розв’язок, що місить інтеграли від розв’язків однорідного лінійного диференціального рівняння, в термінах В.В. Кучеренка - «фазові ланцюжки» [3, стор. 309 ].

Побудуємо m – наближення Xm(t, e) [3, 4], обриваючи формальні ряди для xk(t, e) так, щоб у виразі для x0(t, e, C(k)) взяти 3(m – k) доданків: .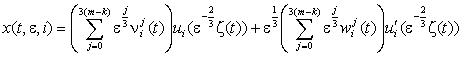

Тоді при підстановці Xm(t, e) у рівняння (1) дістанемо:

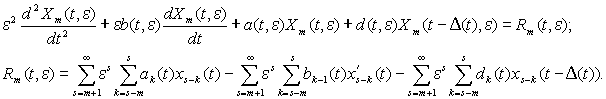
Згідно з оцінками [1, 3, 5] функцій ui(t) та ui¢(t) отримуємо наступну оцінку:

,                                                     (5)

де С – стала, що не залежить від e. Нехай x(t, e) – деякий точний розв’язок задачі (1), (2). Позначивши z(t, e) = x(t, e) – Xm(t, e), переконуємося, що внаслідок побудови Xm(t, e) справджується рівність

.

          Розв’язуючи останнє рівняння при нульових початкових умовах z(0, e) = 0, ez¢(0, e) = 0 методами [2, 4, 5] з урахуванням оцінки (5), переконаємося у правильності наступної теореми.

Теорема. Якщо виконуються умови 10, 20, (3), то рівняння (1) на проміжку [0, L] має формальний розв’язок (4) такий, що для деякого точного розв'язку x(t, e) задачі (2) і m – наближення, отриманого із формального розв'язку, справджується нерівність

,

де C – стала, що не залежить від e, k = 0, 1.

Література:

1.     Ломов С.А. Введение в общую теорию сингулярных возмущений. – М.: Наука, 1981. – 400 с.

2.     Менько Я.П., Фещенко С.Ф. О решении линейного неоднородного дифференциального уравнения второго порядка с медленно меняющимися коэффициентами и запаздывающим аргументом. – В кн.: Первая лет. мат. школа (Канев, июнь – июль 1963 г.). – Киев: Ин-т математики АН УССР, 1964, вып. 2, с. 28-30.

3.     Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. - М.: Наука, 1983. – 352 с.

4.     Фещенко С.Ф., Шкиль Н.И., Пидченко Ю.П., Сотниченко Н.А. Асимптотические методы в теории линейных дифференциальных уравнений с отклоняющимся аргументом. - К.: Наук. думка, 1981. – 296 с.

5.     Шкиль Н.И., Старун И.И., Яковец В.П. Асимптотическое интегрирование линейных систем дифференциальных уравнений с вырождениями. – К.: Выща шк., 1991. – 207 с.