Мельник В.Н., Лозовик Т.Н., Заброда А.А., Саверченко В.Г.

Национальный технический университет Украины «КПИ»

КОЛЕБАНИЯ ТЕНЕВОЙ СТОРОНы ИЗОТРОПНОЙ ПЛАСТИНы В АКУСТИЧЕСКОЙ СРЕДЕ

Наличие плоских фрагментов в элементной базе приборов инерциальной навигации может существенно сказаться на соответствии их характеристик Паспортным требованиям. Речь идет о генерируемых изгибных колебаниях в пластинах под действием проникающего акустического излучения высокой интенсивности. В совокупности с другими факторами, это явление может привести к появлению погрешностей измерений. В частности, при возникновении волнового совпадения.

При составлении математической модели прохождения звука будем исходить из следующих допущений – линейные элементы пластины, перпендикулярные к ее срединной поверхности, при деформировании остаются прямыми, и устанавливаются нормально к искривленной срединной поверхности; в срединной поверхности не возникают деформации удлинения или сдвига; деформации пластины при изгибе остаются малыми, упругими и подчиняющимися закону Гука (Hooke).

Природу изучаемого явления будем изучать на примере плоской монохроматической волны давления, т.е. волны с плоским фронтом, давление и скорость перемещения частиц среды в которой не имеют градиента вдоль линии фронта. Кроме того, скорость частиц среды в плоской волне будем считать пропорциональной давлению в тот же момент времени. На практике, плоскую волну рассматривают как идеализацию волны, излучаемой телом конечных размеров, но находящемся на достаточно большом удалении.

Вопросы прохождения звука через две пластины, не связанные между собой, рассматривал А. London, а более общая теория влияния звука на составные конструкции изложена в ряде монографий.

Если в отмеченных работах изучался вопрос взаимодействия звука с преградой в плане определения ее звукоизоляционных свойств, то здесь основным аспектом исследований являются динамические характеристики пластины при акустическом нагружении.

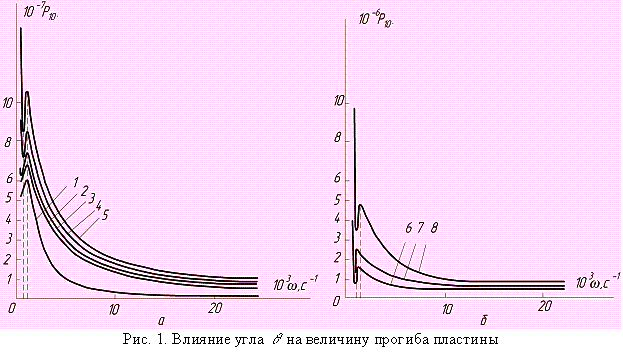
Амплитуда прогиба пластины с возрастанием частоты убывает по экспоненциальному закону, но с увеличением угла падения существенно растет по абсолютному значению (рис. 1). Объяснение этому факту состоит в усилении влияния антисимметричной составляющей, приводящей к «раскачке». Интенсивное движение пластины способствует более мощной трансляции звуковой энергии из одного полупространства в другое.

Плоская волна является, в некотором смысле, идеализированной схемой явления. Более приближенным к натурным условиям представляется диффузное поле, когда вероятность падения звуковой волны одинакова для всех значений угла . Проведя несложную операцию осреднения по Пэрису,

,

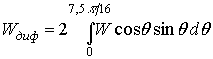можно установить закон изгибного движения пластины при равновероятностном переносе звуковой энергии.

Численный анализ говорит о том, что при прочих равных условиях, в диффузном поле амплитуда изгибной волны с увеличением частоты также уменьшается по экспоненциальному закону.

Быстрота уменьшения более значительная на частоте , причем происходит с одновременным изменением фазы колебаний на .

Для решения целого ряда задач необходимо знать степень влияния частоты на коэффициент отражения звука (рис. 2 ). На диаграмме

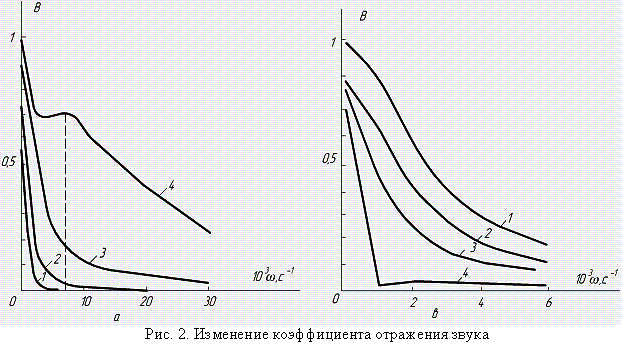
представлены его значения для разных толщин пластины (рис. 2, а), а также для различных углов падения волны (рис. 2, б).

На рис. 2, а приняты следующие обозначения графиков: м; м; м; м.

На рис. 2 б обозначено: ; ; ; .