Удк 513.83
Моделирование движения газа через слой жидкости на тарельчатых колонных аппаратах
Кумисбекова
Б., Каугаева А.М., Ташимов Л.Т.
Международный Казахско-Турецкий университет
им.Х.Ясави, г.Шымкент, Казахстан,
Тарельчатые колонные
аппараты широко используются в различных отраслях химической и нефтехимической
промышленности в качестве очистных аппаратов и аппаратов для переработки нефти.
Несмотря на большой опыт в области проектирования и эксплуатации таких
аппаратов, некоторые проблемы с методиками расчета и поиском оптимальных
конструктивных и режимных параметров остаются не до конца решенными. Это, в
первую очередь, относится к проблемам масштабного перехода, обусловленного
изменением гидродинамических характеристик и
структуры потоков при масштабировании колонн.
В настоящей работе
предлагается для обсуждения новая модель взаимодействия газового потока со
слоем жидкости на провальных тарелках колонных аппаратов химической
промышленности. Целью данной работы явилось описание вихревых структур в зонах
отверстий для слива жидкости и
выделение, позволяющих управлять формированием
гидродинамических режимов. обеспечивающих стабильность работы аппарата.
Пусть ![]() - перепад давления на
слое,
- перепад давления на
слое, ![]() - объемный расход газа через слой.
- объемный расход газа через слой.
В
качестве геометрического критерия порозности слоя по газовому потоку примем (рисунок
1):
![]() (1)
(1)
Этот параметр выглядит следующим образом. Параметр выражен через долю
свободного сечения ![]() :
:
![]() (2)
(2)
Запишем перепад давления в
виде:
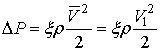 . (3)
. (3)
Из уравнения Бернулли получаем:
![]() (4)
(4)
Баланс массы через отверстие:
![]() .
(5)
.
(5)
Интенсивность вихря, индуцируемого при обтекании
решетки можно принять равной (по крайней мере, по порядку) циркуляции
воздушного потока вокруг элемента решетки с характерным размером ![]() :
:
![]() , (6)
, (6)
здесь
![]() -некоторый
коэффициент, учитывающий особенности обтекания кромки отверстия. По данным [1,
2]
-некоторый
коэффициент, учитывающий особенности обтекания кромки отверстия. По данным [1,
2] ![]() . С другой стороны, из
баланса сил в стационарном состоянии получаем:
. С другой стороны, из
баланса сил в стационарном состоянии получаем:
![]() , (7)
, (7)
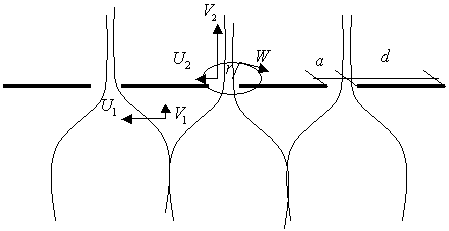
Рисунок 1 - Схема течения газа
Запишем распределение скорости газа в зоне вихря, выраженное через циркуляцию потока в форме:
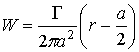 .
(8)
.
(8)
Мощность, диссипируемая в зоне вихря:
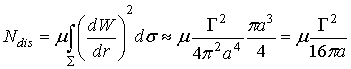 .
(9)
.
(9)
С другой стороны, эту мощность можно оценить из соотношения:
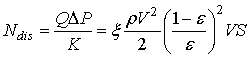 , (10)
, (10)
где
коэффициент ![]() определяется степенью
поджатия струи газа при выходе из отверстия,
определяется степенью
поджатия струи газа при выходе из отверстия, ![]() - число отверстий в
решетке.
- число отверстий в
решетке.
Тогда получаем выражение для интенсивности циркуляции:
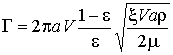 , (11)
, (11)
Далее, используя (10) и (11), находим:
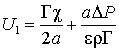 ,
(12)
,
(12)
Отсюда получаем:
![]() , (12)
, (12)
где
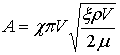 ;
; 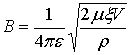 . (13)
. (13)
Для фиксированной доли свободного сечения зависимость поперечной
составляющей скорости газа под решеткой приобретает вид, показанный на рисунке
2.

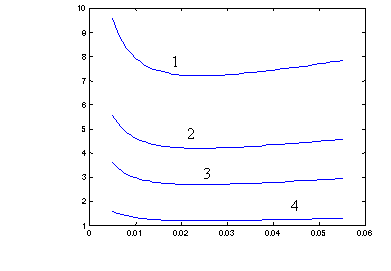
Диаметр
отверстия а, м
Газ - воздух
при нормальных условиях, ![]() м/с.
м/с.
1- ![]() ; 2-
; 2- ![]() ; 3-
; 3- ![]() ; 4-
; 4- ![]()
Рисунок
2 – Зависимость поперечной составляющей скорости газа U1 от
диаметра отверстия а
Минимальное значение поперечной составляющей, которое соответствует минимуму
гидродинамического сопротивления, наблюдается при фиксированной доле свободного
сечения для отверстий с характерным размером:
![]() . (14)
. (14)
Частота обновления межфазной поверхности в рамках предлагаемой модели
может быть описана с помощью уравнения вынужденных колебаний Дюффинга для
тонкого слоя жидкости [3, 4]. Собственную частоту колебаний тонкого слоя
жидкости оценим по соотношению:
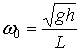 , (15)
, (15)
где
![]() - характерный продольный размер жидкой пленки. Тогда
соответствующее уравнение вынужденных колебаний слоя запишем в виде:
- характерный продольный размер жидкой пленки. Тогда
соответствующее уравнение вынужденных колебаний слоя запишем в виде:
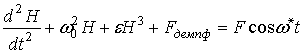 , (16)
, (16)
где ![]() - малый параметр,
характеризующий нелинейность взаимодействия.
- малый параметр,
характеризующий нелинейность взаимодействия.
Оценку величины этого параметра можно
дать в виде:
![]() . (17)
. (17)
Здесь
![]() -амплитуда возмущенного движения жидкой пленки,
-амплитуда возмущенного движения жидкой пленки, ![]() - демпфирующая сила, обусловленная вязкой диссипацией и
влиянием стабилизатора слоя,
- демпфирующая сила, обусловленная вязкой диссипацией и
влиянием стабилизатора слоя, ![]() -амплитуда вынуждающей силы,
-амплитуда вынуждающей силы, ![]() -частота вынуждающей силы.
-частота вынуждающей силы.
Для вынуждающей силы будем рассматривать воздействие газового потока,
проходящего через отверстия тарелки. Тогда частоту вынуждающих колебаний
определим по величине циркуляции газового потока:
![]() . (18)
. (18)
Подставляя в (18) выражение для циркуляции, получаем:
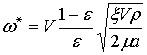 . (19)
. (19)
Амплитуду вынуждающей силы найдем через диссипируемую в слое энергию:
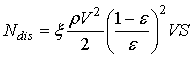 . (20)
. (20)
Тогда получаем оценку:
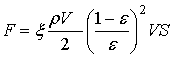 . (21)
. (21)
Будем далее считать, что малый параметр имеет порядок:
![]() . (22)
. (22)
Вывод уравнения последующих соотношений основан на разложении уравнения
колебаний общего вида:
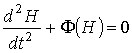 . (23)
. (23)
Разложим в ряд Тейлора в окрестности положения равновесия, где ![]() - возвращающая сила. При этом:
- возвращающая сила. При этом:
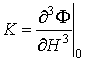 ;
; 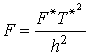 . (24)
. (24)
Здесь ![]() - характерная сила соударения;
- характерная сила соударения; ![]() - характерное время соударения.
- характерное время соударения.
Анализ
уравнения (24) проводится с помощью асимптотических методов разложением по
малому параметру. Применение метода многих масштабов показывает, что при этом в
описываемой системе возникает главный резонанс, наблюдаемый при ![]() , а также ряд вторичных резонансов, характерных для
нелинейного взаимодействия. Для упрощения анализа введем ряд замен переменных
для приведения уравнений к безразмерному виду:
, а также ряд вторичных резонансов, характерных для
нелинейного взаимодействия. Для упрощения анализа введем ряд замен переменных
для приведения уравнений к безразмерному виду:
![]() ;
; 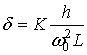 ;
; 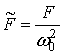 ;
; 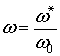 ;
; ![]() (25)
(25)
Тогда уравнение (23) приобретет вид:
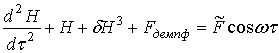 . (26)
. (26)
Выражение демпфирующей силы стабилизатора слоя через скорость изменения
высоты слоя жидкой фазы на тарелке:
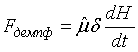 , (27)
, (27)
где
![]() - приведенный
коэффициент сопротивления стабилизирующего устройства:
- приведенный
коэффициент сопротивления стабилизирующего устройства:
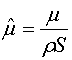 . (28)
. (28)
Основное уравнение движения слоя (20) тогда преобразуется к виду:
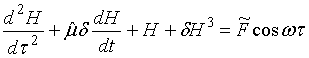 ,
(29)
,
(29)
Здесь ![]() - плотность жидкости,
- плотность жидкости, ![]() - поперечное сечение стабилизирующего устройства.
- поперечное сечение стабилизирующего устройства.
Рассмотрим стационарные колебательные режимы движения пленки, обусловленные
взаимодействием слоя с вихревым потоком газа через отверстия тарелки. Для этого
приближенное аналитическое решение уравнения колебаний слоя будем искать в виде
асимптотического разложения по малому параметру ![]() :
:
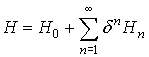 . (30)
. (30)
Для нулевого и первого порядков разложения получаем следующие уравнения:
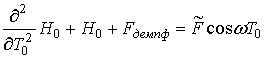 , (31)
, (31)
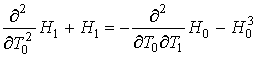 . (32)
. (32)
Решение уравнения (32) можно записать в комплексной форме в виде (здесь
![]() - символ мнимой единицы):
- символ мнимой единицы):
![]() . (33)
. (33)
Далее комплексно сопряженные слагаемые будем обозначать чертой сверху
над буквой. Для амплитуды свободных и вынужденных колебаний слоя соответственно
получаем:
![]() ;
; 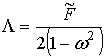 . (34)
. (34)
В итоге получаем систему уравнений для амплитуды и фазы колебаний:
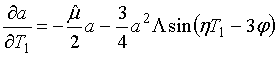 ; (35)
; (35)
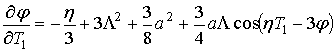 .
(36)
.
(36)
Для этой системы из условий стационарности 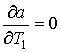 и
и 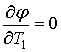 получаем амплитудно-частотную
характеристику системы: «слой жидкости – поток газа на тарелке»:
получаем амплитудно-частотную
характеристику системы: «слой жидкости – поток газа на тарелке»:
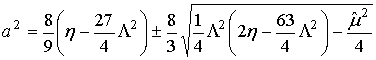 . (37)
. (37)
Действительные решения существуют только в случае выполнения неравенства:
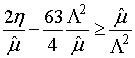 . (38)
. (38)
Введем обозначения: 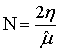 и
и 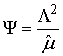 .
.
Стационарные колебания возможны только при некотором отклонении частоты внешней силы, обусловленной вихревым
потоком газа. Из условия минимума функции:
![]() (39)
(39)
находим
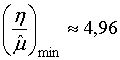 . (40)
. (40)
С помощью этих результатов можно рассчитать параметр обновления
межфазной поверхности при взаимодействии вихревого потока газа со слоем жидкости.
При этом в формулу предлагается подставлять в качестве характерного времени
взаимодействия величину:
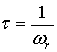 , (41)
, (41)
где
![]() - наблюдаемая частота колебаний пленки, определяемая
характером резонанса.
- наблюдаемая частота колебаний пленки, определяемая
характером резонанса.
Таким образом, можно сделать вывод, что разработанная модель позволяет
рассчитать основные динамические характеристики процесса взаимодействия
газового потока со слоем жидкости на провальной тарелке колонного аппарата.
Большой выбор управляющих параметров: как конструктивных, так и режимных, открывает широкие
возможности при идентификации параметров и позволяет рекомендовать эту модель для инженерных расчетов с учетом
масштабных факторов.
Литература
1
Бельцер Н.И. Олевский
В.М., Кочергин Н.А. К вопросу о масштабном переходе для колонн с регулярной
пакетной гофрированной насадкой: Труды Всесоюзной конференции по
аэрогидродинамике химических аппаратов «Аэрохим-I».-Северодонецк, -1981.-С.89-94.
2
Brener A.M. Adaptation of random walk methods to the modeling of liquid
distribution in packed columns//International Series on Advances in Fluid
Mechanics, IV, WIT Press, Southampton, Boston.-2002,-P.290-300.
3
Linde H., Loeschcke K. Rolling cells and oscillation in heat transfer
between gas and liquid. // Chem. Ing. Techn. 1978 -Vol. 39.- P.65.
4
Pishner A., Shapiro M., Rubin H. A new solution
for the nonlinear diffusion-convection equation // SIAM J. Appl. Math. -1991.
-Vol. 51, № 6. -P.1616.