Д.ф.-м.н. Калимолдаев М.Н., Амирханова Г.А., Гречко С.М.

Институт проблем информатики и управления, Алматы, Казахстан

Об одной задаче глобальной асимптотической устойчивости связанной фазовой системы с нелинейным регулятором

В данной работе исследуется устойчивость и стабилизация движения одной из моделей многомерных фазовых систем, описываемых дифференциальными уравнениями, правые части которых периодичны по угловой координате. Вывод уравнения движения многомерных фазовых систем, описывающих процессы в электроэнергетических системах, а также уравнения регулятора типа «котел-турбина» приведены в [1].

Целью данной работы является решение задачи глобальной асимптотической устойчивости электроэнергетических систем с нелинейным регулятором.

Рассмотрим общую модель многомерных фазовых (электроэнергетических) систем [2]:

(1)

(2)

где функция

(3)

определяет связь между подсистемами и – заданная непрерывно дифференцируемая периодическая функция.

Системы (1), (2) записаны в векторно матричной форме.

Здесь

где – угловая координата; - угловая скорость; - -вектор состояния регулятора; - управляющее воздействие регулятора;  - коэффициент демпфирования; , , - постоянные - мерные векторы; - постоянная - матрица; - управление типа обратной связи. Символ (*) означает операцию транспонирования.

Дифференциальные уравнения второго порядка (1) описывают процессы в объекте управления, а векторные дифференциальные уравнения (2) определяют состояние регулятора -й изолированной подсистемы.

Стационарное множество связанной системы (1) – (2) определяется как множество

(4)

Здесь точка ()= также является стационарной точкой и ближайшие к ней стационарные точки слева и справа определяются как

(5)

Рассмотрим глобальную асимптотическую устойчивость движения связанной системы со многими угловыми координатами в случае

, (6)

где , – постоянные, – векторы, - скалярная постоянная.

При этом системы (1) –(2) принимают вид

(7)

(8)

или в векторно-матричной форме

₍₉₎

(10)

где

Характеристика нелинейных элементов: - непрерывные функции, удовлетворяющие условиями:

Если для функции имеют место неравенства вида

то после замены придём к рассматриваемому случаю, при этом . дифференциальные уравнения (8) перепишутся в виде:

где, нелинейность удовлетворяет условию:

_.

Ограничение (10) равносильно неравенству

. (11)

Функция

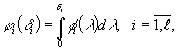(12)

Является положительной полуопределенной функцией.

Предположим, что стационарное множество системы (9), (10) определятся соотношением (4).

Введём в рассмотрение симметрические – матрицы - векторы , скаляры и обозначим

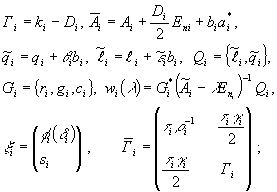(13)

.

Обозначим также через

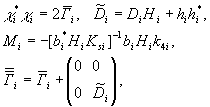(14)

где – матрицы, – матрицы.

Используя эти обозначения, сформулируем следующую теорему.

Теорема. Пусть существуют скаляры,, такие, что:

1) Фазовая система второго порядка глобально асимптотически устойчива (т.е.);

2) – полностью наблюдаемая пара;

3) Матрица – гурвицева;

4) –полностью управляемая пара;

5)

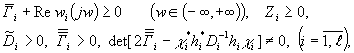
Тогда управление

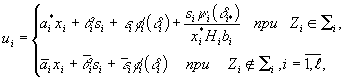(15)

обеспечивает глобальную асимптотическую устойчивость движения системы (9), (10).

Заключение. В данной работе для электроэнергетической системы с нелинейным регулятором выведены достаточные условия глобальной асимптотической устойчивости движения на основе метода нелокального сведения Леонова [3]. Эти условия получены с помощью - процедуры Лурье, частотной теоремы Якубовича-Каллмана и теории особых управлений.

Литература

1. Андерсон П., Фуад А. Управление энергосистемами и устойчивость. – М.: Энергия, 1980. – 568 с.

2. Бияров Е.Н., Калимолдаев М.Н. Глобальная асимптотическая устойчивость многомерных фазовых систем с нелинейным регулятором // Обратные задачи динамики и их приложения. – Алма-Ата: Изд.-во КазГУ, 1986. – С. 12-17.

3. Гелиг А.Х., Леонов Г.А., Якубович В.А. Устойчивость нелинейных систем с неединственным состоянием равновесия. – М.: Наука, 1978. – 400 с.