к.ф.-м.н. А.И. Долгарев

ГЕОМЕТРИЯ ВО-ПРОСТРАНСТВ И ГЕОМЕТРИЯ ГРУПП ЛИ

Обе геометрии имеют общую основу – они построены на группах Ли и используют общую аксиоматику Г. Вейля. однако представляют собой различные теории. Анализируется различие этих геометрий.

1. Разные геометрии одной группы

На одной и той же группе в одной и той же аксиоматике имеются различные геометрии. На одной и той же алгебраической структуре действительном линейном пространстве в одной и той же аксиоматике Г. Вейля получены принципиально различные геометрии. Это, например, собственно евклидова геометрия и псевдоевклидова геометрия. Их основой является аффинное пространство с линейным пространством . Можно ограничиться случаем действительных пространств, т.е. случаем линейного пространства над полем действительных чисел .

Для множества точек аффинного пространства рассматривается отображение пар точек в линейное пространство . Всякой паре точек из соответствует единственный вектор из , указанный вектор обозначается , т.е. . Отображение

удовлетворяет двум условиям, которые называются аксиомами Г. Вейля.

(В.1) Для всякой точки и всякого вектора существует единственная

точка , что .

(В.2) Для любых трех точек , если , , то .

Геометрические свойства множества точек являются следствием алгебраических свойств его линейного пространства , точнее следствием аксиоматики линейного пространства.

Аффинное пространство не обладает метрическими свойствами. Имеется возможность для реализации измерений во множестве точек. Можно во множестве ввести отображение в :

,

т.е. ввести метрическую функцию , потребовав выполнения соответствующих условий, например:

и .

Наличие векторов при этом не обязательно. Имея линейное пространство, можно использовать скалярное произведение векторов. В этом случае расстояние между точками и определяется как корень квадратный из скалярного квадрата вектора . Указанный способ является общим для многих пространств.

Метрические свойства собственно евклидова и псевдоевклидова пространств кардинально различны. Общий подход к определению метрики весьма полезен во многих вопросах, однако различия в частностях могут быть существенными. Не все свойства собственно евклидова скалярного произведения векторов переносятся на псевдоевклидово скалярное произведения векторов.

Относительно внутренней операции, т.е. операции сложения, векторы из составляют группу Ли. Группа Ли очень проста по своей структуре. На этой группе Ли в аксиоматике Г. Вейля получены многие геометрии: евклидовы [1], римановы [2], галилеевы [3]. Дело не только в группе Ли , но и в применяемых методах исследования, в условиях, наложенных на объекты и отображения и т.д.

2. Алгебраические структуры с общим носителем

Хорошо известно, что различаются свойства алгебраических структур с общим носителем и различной сигнатурой. Более того, рассматривая на алгебраической структуре дополнительные операции, получаем другие алгебраические структуры и дополнительные возможности, хотя бы в методах исследования. Например, различны теория абелевых групп и теория модулей над кольцами. В руководствах по общей алгебре содержатся в качестве различных разделов теория абелевых групп и теория модулей, см., например, оба тома СМБ [4]. На свойствах модулей лежит отпечаток свойств колец, над которыми модули определены. Еще более разителен отпечаток свойств полей на абелевых группах в теории линейных пространств.

Обозначим вешнюю операцию над структурой на структуре через . На носителе имеется сигнатура , состоящая из двух операций – одной внутренней и одной внешней. Таким образом, имеются различные алгебраические структуры и . Если абелева группа с операцией *, обычно называемой сложением, кольцо, то есть модуль над кольцом . Если кольцо является, в частности, полем, то алгебраическая структура есть линейное пространство над полем .

На произвольной группе , не обязательно абелевой, посредством внешней операции определяется другая алгебраическая структура. Известна группа над кольцом, [4, c. 104 – 105]. Во внешней операции производится умножение элементов группы на скаляры из кольца . Имеется структура , требуется выполнение следующих аксиом (кроме аксиом группы). Для любых выполняются равенства:

;

где 0 и 1 – нулевой и единичный элементы кольца (если кольцо унитарно), нулевой элемент группы;

; ;

.

На структуре группы определены еще структуры кольца, тела . На носителе группы рассматривается еще одна внутренняя операция , она связана с операцией сложения свойством дистрибутивности.

Обобщением структуры модуля над кольцом является структура одуля над кольцом, введенная Л.В. Сабининым, [5]. Обобщение довольно широкое, в качестве исходной выбрана произвольная алгебраическая структура с одной внутренней операцией , операцию уместно называть сложением. Л.В. Сабинин рассматривал квазигруппы и умножение элементов квазигрупп на скаляры из кольца . Требуется выполнение аксиомы . Полученную структуру Л.В. Сабинин называет одулем над кольцом . Возникла структура одуля в вопросах приложений квазигрупп и луп в геометрии. -одули на квазигруппах и лупах оказались очень востребованными, о чем свидетельствуют многочисленные работы различных авторов во всем мире, см., напимер, [6, 7]. В частности, при дополнительных условиях, квазигруппа может быть группой; в этом случае речь идет об одуле на группе, тогда этот термин совпадает с термином группы над кольцом из [4]. Если одуль определен на группе Ли, то он называется одулем Ли, термин из [3]. Л.В. Сабинин рассматривает аналитические лупы и одули на них, что обобщает группы Ли и одули Ли. Последние относятся к аналитическим одулям, т.е. к одулям на лупах над телом (полем).

Итак, группы Ли и одули Ли являются сугубо различными алгебраическими структурами. В частности, различны, например, группы векторов и линейные пространства над телом (полем).

3. Одули Ли аффинных преобразований

Аксиома (В.1) аффинного пространства определяет на аффинном пространстве аффинные преобразования. Зафиксировав вектор и перебирая точки аффинного пространства, получаем множество пар точек , соответствующее вектору из в отображении . Каждая точка в этом соответствии имеет единственный образ, разные точки имеют разные образы.

Пусть точки попарно различны, , . Для точки и вектора существует единственная точка , что . Из (В.2) следует . Таким образом, вектор можно интерпретировать как параллельный перенос аффинного пространства, это аффинное преобразование аффинного пространства. В композиции преобразований и , преобразования перестановочны, группа параллельных переносов абелева. На группе

определена внешняя операция умножения параллельных переносов на действительные числа и линейное пространство переносов является абелевым одулем Ли. В [8] установлено, что аффинные преобразования плоскости составляют одуль Ли. Это верно и для аффинных преобразований мерного аффинного пространства . Пододули аффинного одуля дают многочисленные примеры коммутативных и некоммутативных одулей Ли преобразований, [3]. К ним относится растран (греческая буква ро) – одуль параллельных переносов и гомотетий аффинного пространства, сибсон – одуль галилеевых движений, и т.д..

4. Геометрия ВО-пространств

Заменяя в аксиоматике Г. Вейля линейное пространство одулем Ли =, имеем вейлевское одулярное пространство , коротко ВО-пространство, [3]. Первое некоммутативное ВО-пространство определено в [9], это ВО-пространство с 3-мерным растраном.

На растране, с использованием его специфики, определена галилеева норма растов – элементов растрана. Эта специфика есть следствие операций над растами. Расты представлены тройкам действительных чисел – носитель растрана есть . Пусть и произвольные расты. Операции над растами определены равенствами

;

=; ; .

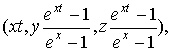
Нулевой раст есть ; раст, противоположный расту , равен = . [3, c. 107]. Сложение растов некоммутативно. В записи операции сложения усматривается операция правого сдвига на растране, что дает представление растов матрицами:

,

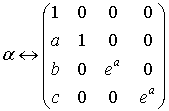т.е. расту соответствует аффинное преобразование аффинного пространства с выписанной матрицей. Сложению растов, представленных тройками из , соответствует произведение матриц:

= .

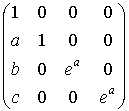
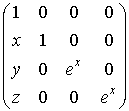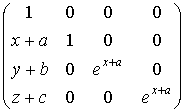Таким образом, для растрана имеются арифметическая и матричная модели.

В первой модели можно строить аналитическую геометрию ВО-пространства с растраном, которое названо ЛМ-пространством.

Пусть множество точек, всякая точка есть тройка из : . Имеется нулевая тройка . Паре точек соответствует раст , паре , если , соответствует раст ,

= .

Прямая линия в ЛМ-пространстве определяется точкой и растом , обозначение: . Прямая обладает 1-мерным подрастраном – оболочкой раста , и является множеством точек

.

Параметрические уравнения прямой :

, , .

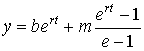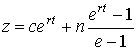Уравнения нелинейны, что основано на операциях над растами.

Через всякие две различные точки ЛМ-пространства проходит единственная прямая. Прямые и либо совпадают (если ), либо не имеют общих точек (если ). Если , то . При прямые и не имеют общих точек. Существует два вида параллельности прямых: параллельны прямые с общим подрастраном и прямые с сопряженными подрастранами.

Пусть расты независимы, т.е. . Плоскостью называется множество точек

.

Через всякие три неколлинеарные точки ЛМ-пространства проходит единственная плоскость. В плоскости через точку , не лежащую на прямой , лежат обе прямые и , параллельные прямой , где . Уравнения плоскости нелинейны. Параллельность плоскостей определяется аналогично параллельности прямых.

Существует 2-мерное ЛМ-пространство, т.е. ЛМ-плоскость.

В операции сложения растов в компоненты троек неравнозначны, что и выявляет специфику растрана. Поэтому на растране определяется галилеево скалярное произведение растов, см. [3, c. 119 – 121].

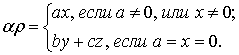
Скалярный квадрат раста равен

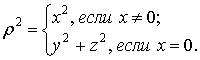
Нормой раста называется . Имеем галилееву норму:

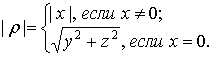
Первая компонента растов является временной, оставшиеся компоненты являются пространственными. Расстояние между точками , , определяемое как норма раста , равно

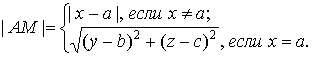
Первые компоненты точек являются временными, оставшиеся – пространственными. ВО-пространство с нормированным растраном является галилеевым пространством-временем с некоммутативной геометрией. Пространство с нормированным растраном называется ЕМ-пространством и обозначается .

Растранная функция

,

непрерывна в точке , если действительные функции непрерывны в точке . Функция непрерывна на интервале, если она непрерывна в каждой точке интервала. Производной функцией функции называется предел в каждой точке интервала :

.

Приращение функции определяется из равенства ,

=.

Вычисления приводят к следующей формуле дифференцирования:

.

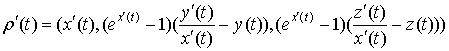Обычные правила дифференцирования векторных функций на растранные функции не распространяются; , .

Возможность дифференцировать растранные функции позволила построить дифференциальную геометрию ЕМ-пространства, аналогичную евклидовой дифференциальной геометрии. Кривая ЕМ-пространства называется регулярной класса , если существуют производные функции до третьего порядка включительно, , непрерывна.

Ввиду регулярности линии, временная компонента обратима и регулярная кривая задается в естественной параметризации функцией:

=, .

По определению нормы растов,

.

В дифференциальной геометрии пространства с растраном вводятся основные понятия по аналогии с понятиями евклидовой дифференциальной геометрии и получены результаты, аналогичные результатам евклидовой дифференциальной геометрии. Доказана основная теорема теории кривых об определяемости кривой ее натуральными уравнениями, т.е функциями кривизн, [10], основная теорема теории поверхностей об определяемости поверхности коэффициентами ее первой и второй квадратичных форм, [11].

Растран является разрешимым ступени 2 3-мерным действительным одулем Ли. Существует еще три некоммутативных разрешимых 3-мерных одуля Ли: сибсон (одуль Ли галилеевых движений плоскости), диссон (вместе с сибсоном являющийся расширением мультипликативной группы дуальных чисел), осцилляторный одуль (одуль Ли евклидовых движений плоскости). Перечисленные одули Ли являются пододулями одуля Ли аффинных преобразований пространства. В [3] изложены галилеевы дифференциальные геометрии пространств с растраном, сибсоном и диссоном, где проведена аналогия с евклидовой дифференциальной геометрией. В указанном изложении преодолены значительные трудности; в отличие от растрана, сибсон и диссон являются 2-порождеными одулями Ли. В пространствах с сибсоном и диссоном не через каждые три неколлинеарные точки проходит плоскость. Однако, основные теоремы теории кривых и теории поверхности в этих пространствах имеют место.

Выяснилось, что не существует дифференциальной геометрии пространства с осциииилляторным одулем Ли, т.к. осцилляторные функции не дифференцируемы, [12].

На растране может быть введена метрика, похожая на евклидову. Такая метрика на группе Ли предложена в [13, c. 127], эта группа Ли определяет геометрию многообразия Sol. Таким образом возможна не только галилеева геометрия ВО-пространств.

5. О геометрии групп Ли

Основоположником геометрии групп Ли является Э. Катан, начала теории содержатся в его статьях, переводы на русский язык которых составляют [14]. Остановимся на начальных положениях из [14].

Э. Картан рассматривает непрерывную параметрическую группу преобразований . Набор значений параметров интерпретируется как точка , множество всех точек называется групповым пространством ﻉ. Каждой точке соответствует преобразование из группы . Вектором группового пространства называется пара точек . [Задано отображение пар точек группового пространства ﻉ в группу преобразований .] (Текст в квадратных скобках является комментарием автора к работам Картана.) Свойства указанного отображения определяются группой . [Эти свойства включают в себя и условия (В.1),(В.2). Следовательно, геометрия группового пространства ﻉ строится в аксиоматике Г. Вейля, в которой линейное пространство заменено непрерывной группой преобразований .] Рассматривается два вида равенства векторов, что является следствием некоммутативности группы .

Геодезические линии группового пространства ﻉ определяются 1-параметрическими подгруппами группы . [В ВО-пространствах это прямые линии. ВО-пространство с одулем Ли = является соответственно одулярным пространством одуля Ли ; его можно считать групповым пространством группы Ли . Все ВО-пространства, рассматриваемые в [3], своими одулями имеют пододули одуля Ли аффинных преобразований аффинного пространства .] Два вида равенства векторов приводят к двум видам параллельности геодезических линий группового пространства. [Что соответствует двум видам параллельности прямых в ВО-пространствах.] Рассматриваются вполне геодезические многообразия группового пространства ﻉ, определенные порожденными подгруппами группы . [При имеем плоскости в ВО-пространствах в случае, если 2-порожденный пододуль является 2-мерным.]

Сказанное означает, что ВО-пространства могут быть отнесены к групповым пространствам групп Ли при условии, что на группах Ли не рассматриваются внешние операции. ВО-пространства составляют более узкий класс пространств, чем класс групповых пространств. Геометрия ВО-пространств есть специфический частный случай геометрии групп Ли.

Интересно было бы изучать геометрии абелевых групп Ли, ведь абелевы группы не исчерпываются векторными группами . Думается, что это была бы содержательная часть геометрии групп Ли, где общие методы исследований получили бы специализацию, связанную с коммутативностью групповой операции. Имеются квазициклические группы, а также абелевы группы кортежей с нелинейными, т.е. альтернативными, операциями:

.

,

см. [15]. В [16] на 2-мерном альтернативном линейном пространстве рассмотрена альтернативная аффинная плоскость. Группа альтернативных аффинных преобразований отличается от группы аффинных преобразований, согласно Эрлангенской программе Ф. Клейна, геометрия альтернативной аффинной плоскости отлична от аффинной геометрии.

Методы геометрии ВО-пространств существенно используют возможности внешней операции, являются методами дифференциальной геометрии, аналогичными методам евклидовой дифференциальной геометрии, а они принципиально отличаются от методов геометрии групп Ли. В групповом пространстве группы Ли определяются аффинные связности, при этом используются бесконечно малые [инфинитезимальные] преобразования и пфаффовы формы. Кривизна и кручение группового пространства определяются как свойства аффинной и проективной связностей. В геометрии ВО-пространств кривизна линии определена как норма одуляра второй производной одулярной функции, задающей линию в естественной параметризации. Полная кривизна поверхности определяется через коэффициенты ее квадратичных форм поверхности. В [3] изучаются галилеевы геометрии ВО-пространств. В геометрии групп Ли галилеевы геометрии не выделяются.

6. Соотношение геометрии ВО-пространств и геометрии групп Ли

Геометрия ВО-пространств охарактеризована в п. 4, геометрия групп Ли – в п. 5. Как уже отмечено, геометрия ВО-пространств может рассматриваться как своеобразный раздел геометрии групп Ли. Кардинальное отличие геометрий в том, что это геометрии пространств с различными алгебраическими структурами. Можно, например, рассматривать кольцевые пространства и полевые пространства – пространства над кольцами и пространства над полями. Геометрии этих пространств тоже являются разделами геометрии групп Ли, т.к. на группах Ли можно ввести дополнительную внутреннюю операцию умножения, получив – структуру кольца или поля. Имеется и дальнейшее углубление в рассматриваемые геометрии в результате введения внешних операций на .

Кардинальное отличие геометрии ВО-пространств и геометрии групп Ли состоит в методах исследования, как отмечалось в предыдущем п. 5. Геометрия ВО-пространств переносит классические дифферециально-геометрические методы евклидовой геометрии на некоммутативные пространства, хотя аксиоматика всех рассматриваемых пространств общая – аксиоматика Г. Вейля. Метрика в ВО-пространствах основана на квазискалярном произведении одуляров. Различаются геометрии ВО-пространств, размерность которых совпадает и не совпадает от числа порождающих элементов одулей Ли. Например, 3-мерный растран 3-порожден, а 3-мерный сибсон 2-порожден. В одулярных пространствах используется одулярный анализ, аналогичный векторному анализу. ВО-пространство с осцилляторным одулем Ли отбраковано, как не обладающее дифференциальной геометрией; в геометрии групп Ли все группы Ли на одно лицо. Общность методов евклидовой и галилеевой геометрий приносит свои плоды. Галилеевы методы с успехом используются в евклидовой геометрии. Они вносят прозрачность в евклидову теорию, [17], и выявляют неизвестные свойства евклидова пространства, в том числе его неоднородность.

Геометрия ВО-пространств настолько специфический частный случай геометрии групп Ли, что выпадает из общего случая. А общую аксиоматику имеют принципиально различные геометрии. ВО-пространства в сочетании с дифференциально-геометрическими методами нетривиально пополняют разнообразие таких геометрий. Геометрия ВО-пространств относится к фундаментальной математике.

Использованная литература

1. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия,- 2-ое изд., перераб. - М.: Наука, 1986, - 304 с.

2. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. - 664с.

3. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

4. Мельников А.В., Ремесленников В.Н., Романьков В.А., Скорняков Л.А.,Шестаков И.П. Общая алгебра. Т.1. - М.: Наука, 1990.- 592 с. (справ. мат. библ.)

5. Сабинин Л.В. Одули как новый подход к геометрии со связностью //ДАН СССР. 1977. N5. C.800-803.

6. Сабинин Л.В., Михеев П.О. Гладкие квазигруппы и геометрия //Проб-лемы геометрии. т.20. ВИНИТИ. М., 1988.- С.75-110.

7. Sabinin L.V. Smooth Quasigroups and Loops.- Kluwer Academie Publishers. Dordrecht. Netherland, 1999, xvi + 250 (English)

8. Долгарев А.И. Одулярное описание аффинных преобразований плоскости. Деп. в ВИНИТИ 02.07.97, № 369 – 97. М. ВИНИТИ, 1997 – 97с.

9. Долгарев А.И. ЛМ-пространство //Римановы пространства и методы эллиптических дифференциальных уравнений. Л.: ЛГПИ, 1986. - С.8-25.

10. Долгарев А.И. Натуральные уравнения кривых 3-мерных одулярных галилеевых пространств.// Дифференциальная геометрия многообразий фигур, Межвуз. тем. сб. научн. тр., Калиниград, КГУ, 2005, вып. 36. - С. 31-36.

11. Долгарев И.А. Получение поверхности 3-мерного галилеева пространства с растраном по коэффициентам ее квадратичных форм. // Известия высших учебных заведений. Поволжский регион. Физико-математически науки, Пенза, 2007, № 6, С. 17 – 31.

12. Долгарев А.И. Недифференцируемый одуль. // Дифференциальная геометрия многообразий фигур, Межвуз. тем. сб. научн. тр., Калиниград, КГУ, 2001, вып. 32. - С. 34-37.

13. Скотт П. Геометрии на трёхмерных многообразиях. -М.: Мир, 1986.- 168 с.

14. Картан Э. Геометрия групп Ли и симметрические пространства. – М.: ИЛ – 1949. – 386 с.

15. Долгарев А.И., Долгарев И.А. Альтернативные действительные линейные пространства размерностей 2,3,4.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза, 2011, № 1(17), С. 3 – 19.

16. Долгарев А.И., Долгарев И.А. Альтернативная аффинная плоскость// Владикавказский математический журнал, т. 9. вып. 4 (октябрь-декабрь), Владикавказ, 2007, С. 4 – 14.

17. Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов// Известия высших учебных заведений. Поволжский регион. Физико-математически науки, - Пенза, 2009, № 2(10), С. 39 - 59.