Биологические
науки/4.Ресурсоведение и интродукция растений
Д.с.-х.н. Колтунова А.И., Паламарчук И.В.,
к.с.-х.н. Паламарчук П.Г.
Оренбургский государственный аграрный университет, Россия
Закономерности текущего изменения линейных показателей в древостоях сосны
обыкновенной
Лес – основной компонент
биосферы, и изучение его жизнедеятельности в условиях глобальных изменений
климата выдвигает на первый план проблемы продуктивности и устойчивости лесных
ценозов, прогнозирования их состояния.
Задачи прогнозирования развития процессов в экосистемах – актуальнейшая
проблема современного ресурсоведения.
Пути их решения возможны на
основе биометрического моделирования. Эмпирические модели локального уровня –
первый этап изучения закономерностей роста и развития лесных ценозов –
представлены в достаточно большом количестве (Усольцев, 2007; Швиденко, 2008).
Обобщение локальных эмпирических результатов с целью выявления общих
закономерностей биопродукционного процесса, абстрагированных от влияния
географических, эдафических и, в определенной мере, климатических
факторов среды – явилось основной
задачей нашей работы.
Основой наших
исследований послужила наиболее полная
на сегодняшний день база данных о биологической продуктивности лесообразующих
пород Северной Евразии (Усольцев,
2002). Из таблиц биологической продуктивности (ТБП) были взяты сосняки в
возрасте от 20 до 120 лет и подсчитан
относительный текущий прирост для линейных показателей показателей: высоты (Н)
и диаметра (D) сосны обыкновенной (Рinus sylvestris L.) по формуле (Колтунова А.И, 2004):
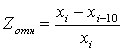 (1) ,
(1) ,
где хi –значение показателя в возрасте i-лет.
Объём полученной выборки составил 38 ТБП с I по V класс бонитета
Второй этап исследований
связан с проверкой гипотезы об однородности относительного текущего изменения
рассматриваемых таксационных показателей по классам бонитета. Проверка
осуществлялась с помощью двух критериев: “хи-квадрат” (Пирсона) и более чувствительного (мощного) критерия проверки гипотезы
Колмогорова-Смирнова.
На третьем этапе
исследований, после объединения данных в одну выборку, были найдены
математические модели.
В качестве аппроксимирующей функции взято уравнение системы кривых Пирсона
(Колтунова, 2004):
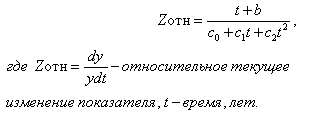 (2),
(2),
На четвертом этапе был
проведён расчёт параметров
математических моделей. Для характеристики каждой математической
модели найден коэффициент детерминации Kd (Кремер и др., 2002), который
численно показывает, на сколько процентов аппроксимируемая модель
отражает фактическую зависимость.
Анализ полученных данных по формуле (1)
(округлено до десятых) показывает: относительные текущие изменения высоты
Zотн(Н) варьируют от 0,5 до 0 как для
нормальных и сомкнутых, так и для модальных и нормальных с прореживаниями
древостоев, имея наибольшее значение в возрасте 30 лет, преимущественно при
более высоких классах бонитета. Причём, начиная с 50 лет, относительный
текущий прирост практически не
отличается и равен 0,2, а в возрасте 60
лет принимает значение 0,1 и лишь при более высоких классах бонитета - 0,2. В
период от 70 до 90 лет, в основном, относительный текущий прирост равен 0,1, а
в 100 лет варьирует между 0,1 и 0. В возрасте 110 и 120 лет относительный
текущий прирост приближённо равен нулю. В качестве примера приведена выборка из
материалов исследований (таблица 1).
Таблица 1- Относительное текущее
изменение высоты Zотн(Н) древостоев по классам бонитета
|
Лесорастительная
провинция; авторы ТХР |
Возраст, лет |
Относительное текущее изменение высоты древостоев по классам бонитета |
||||||||||||||
|
I |
II |
III |
IV |
V |
||||||||||||
|
1* |
2* |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|||||||
|
Скандинавско-Русская провинция, хвойно-широколиственные леса |
||||||||||||||||
|
Нормальные сосняки (P. sylvestris)
Литвы (ТХР: J. Butenas; цит. по: Miško…, 1983) |
30 |
0,3453 |
0,3 |
0,3445 |
0,3 |
0,3535 |
0,4 |
0,3544 |
0,4 |
0,3833 |
0,4 |
|||||
|
40 |
0,2235 |
0,2 |
0,2273 |
0,2 |
0,2385 |
0,2 |
0,2404 |
0,2 |
0,25 |
0,3 |
||||||
|
50 |
0,1517 |
0,2 |
0,1585 |
0,2 |
0,1613 |
0,2 |
0,1746 |
0,2 |
0,1837 |
0,2 |
||||||
|
60 |
0,1097 |
0,1 |
0,1117 |
0,1 |
0,1193 |
0,1 |
0,131 |
0,1 |
0,1404 |
0,1 |
||||||
|
70 |
0,0778 |
0,1 |
0,0844 |
0,1 |
0,0881 |
0,1 |
0,0994 |
0,1 |
0,1163 |
0,1 |
||||||
|
80 |
0,0551 |
0,1 |
0,0586 |
0,1 |
0,0631 |
0,1 |
0,0747 |
0,1 |
0,0915 |
0,1 |
||||||
|
90 |
0,0355 |
0 |
0,044 |
0 |
0,0507 |
0,1 |
0,0595 |
0,1 |
0,0658 |
0,1 |
||||||
|
100 |
0,0276 |
0 |
0,031 |
0 |
0,0398 |
0 |
0,0464 |
0 |
0,0617 |
0,1 |
||||||
|
110 |
0,0203 |
0 |
0,0227 |
0 |
0,03 |
0 |
0,0396 |
0 |
0,0471 |
0 |
||||||
|
120 |
0,0133 |
0 |
0,0186 |
0 |
0,0127 |
0 |
0,0335 |
0 |
0,0449 |
0 |
||||||
|
Средне-Сибирская провинция, средняя тайга |
||||||||||||||||
|
Нормальные сосняки
таежной и лесостепной подзон Цент-ральной и Вос-точной Сибири: обобщенный
норматив (ТХР: Shvidenko et al.,
1996) |
30 |
0,3559 |
0,4 |
0,3458 |
0,3 |
0,3827 |
0,4 |
0,4615 |
0,5 |
0,5862 |
0,6 |
|||||
|
40 |
0,2436 |
0,2 |
0,2357 |
0,2 |
0,2636 |
0,3 |
0,3247 |
0,3 |
0,3958 |
0,4 |
||||||
|
50 |
0,1702 |
0,2 |
0,1667 |
0,2 |
0,1912 |
0,2 |
0,2376 |
0,2 |
0,3043 |
0,3 |
||||||
|
60 |
0,1256 |
0,1 |
0,125 |
0,1 |
0,1392 |
0,1 |
0,1721 |
0,2 |
0,2247 |
0,2 |
||||||
|
70 |
0,0966 |
0,1 |
0,09 |
0,1 |
0,1023 |
0,1 |
0,1286 |
0,1 |
0,1682 |
0,2 |
||||||
|
80 |
0,0739 |
0,1 |
0,0705 |
0,1 |
0,0785 |
0,1 |
0,1026 |
0,1 |
0,1301 |
0,1 |
||||||
|
90 |
0,0586 |
0,1 |
0,0542 |
0,1 |
0,0591 |
0,1 |
0,0714 |
0,1 |
0,1022 |
0,1 |
||||||
|
100 |
0,0455 |
0 |
0,0438 |
0 |
0,0514 |
0,1 |
0,0615 |
0,1 |
0,0805 |
0,1 |
||||||
|
110 |
0,037 |
0 |
0,0309 |
0 |
0,036 |
0 |
0,0479 |
0 |
0,057 |
0,1 |
||||||
|
120 |
0,0262 |
0 |
0,0263 |
0 |
0,0263 |
0 |
0,0359 |
0 |
0,0482 |
0 |
||||||
* 1- расчётные значения относительного текущего прироста;
2- значения относительного текущего
прироста, округленные до десятых.
Показатели относительного текущего
прироста диаметра Zотн(D) изменяются на начальных этапах
регистрации (30-40 лет), в основном, в пределах 0,6-0,2, в трёх случаях
из 38 ТБП достигая своего максимума
(0,6) на III-V классах бонитета. Начиная с 50-ти лет данные показатели изменяются
более плавно: в 50 лет, в основном – 0,2, изредка достигая значения 0,3 при более высоких классах бонитета;
в 60 лет относительный текущий прирост равен 0,2 или 0,1; в период от 70 до 120
лет показатель варьирует от 0,1 до 0. В возрасте 120 лет, в семи из тридцати восьми ТБП, во всех
классах бонитета, относительный текущий прирост близок к нулю.
Сравнение данных относительного текущего изменения линейных
показателей прироста сосны обыкновенной по классам бонитета ТБП показывает, что их величины в различных
условиях местопроизрастания очень мало отличаются друг от друга.
Проверка
гипотезы об однородности относительных текущих изменений линейных показателей
по классам бонитета, по критерию
"хи-квадрат" Пирсона,
показала - наибольшее значение наблюдаемого значения 0,1047, что
меньше критического значения 16,91898
при уровне значимости 0,05 и числе степеней свободы 9. Для критерия
Колмогорова-Смирнова при критическом значение Dкр (0,05) =0,6074 наблюдаемое значение Dнабл изменялось от 0,4 до 0,1.
Статистическое
сравнение рядов относительного текущего изменения высоты и диаметра по классам
бонитета не выявило достоверных различий ни по критерию "хи-квадрат"
Пирсона, ни при использовании критерия Колмогорова-Смирнова. В связи с этим, логично выполнение
анализа географических закономерностей текущего изменения линейных
показателей в древостоях сосны обыкновенной лишь для одного - III (среднего) класса
бонитета рассматриваемых ТБП. В данном
случае наибольший результат наблюдаемого значения критерия
"хи-квадрат" Пирсона
равен 0,1213, что меньше критического значения 16,91898
. Критерий Колмогорова-Смирнова - 0,4,
а критическое значение - 0,6074. .Для всех случаев сравнения выборки из 38 ТБП
древостоев сосны ни по критерию "хи-квадрат" Пирсона, ни по критерию
Колмогорова-Смирнова нулевая гипотеза о принадлежности рядов к одной
генеральной совокупности не была отвергнута.
Анализируя вышеизложенное, можно заключить, что относительные текущие
изменения высоты и диаметра древостоев сосны обыкновенной не
зависят от условий среды и района их произрастания,
но изменяются во времени, что способствует аппроксимации возрастного характера
исследуемого признака.
Соответственно, относительный текущий прирост изучаемых линейных
показателей можно объединить в отдельные выборки большего объема, что приведёт
к сужению доверительного интервала для параметров математической модели, позволяющей аппроксимировать возрастной характер исследуемого признака. В качестве аппроксимирующей функции
использовано уравнение системы кривых Пирсона (2). Параметры
математических моделей изучаемых линейных показателей древостоев сосны
находились средствами Microsoft Excel и приведены в таблице 2, а графическая интерпретация - на рисунке 1.
Таблица 2- Параметры и характеристики моделей роста древостоев естественных
сосняков (для модальных и нормальных с прореживаниями Fкр=2,69; для нормальных
и сомкнутых Fкр=2,64)
|
Показатели |
Параметры уравнения |
Кd |
Fн |
|||
|
b |
c0 |
c1 |
c2 |
|||
|
модальные и нормальные с прореживаниями сосняки |
||||||
|
Zотн(H) |
-177,0549559 |
-7,386323419 |
-11,11016925 |
-0,053733706 |
0,967 |
1043,7 |
|
Zотн(D) |
-176,9034523 |
-7,553843793 |
-14,89138883 |
0,045076459 |
0,916 |
386,96 |
|
нормальные и сомкнутые сосняки |
||||||
|
Zотн(H) |
-177,0267981 |
-7,400061667 |
-11,39201977 |
-0,047914678 |
0,957 |
1975,1 |
|
Zотн(D) |
-176,9186065 |
-7,492755922 |
-13,53754603 |
0,034813078 |
0,900 |
794,1 |
Для оценки адекватности полученных моделей использован критерий Фишера. В результате проверки
выяснено, что во всех случаях модель
адекватна, так как наблюдаемое значение (Fн) больше
критического (Fкр) (таблица 2).
Рисунок
1–Динамика относительного текущего изменения высоты древостоев модальных
и нормальных с прореживаниями сосняков
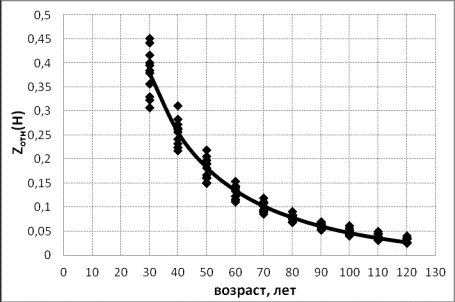
Для каждой математической модели был найден коэффициент детерминации Кd, который
варьировал от 0,90 до 0,97, что говорит о высокой точности аппроксимации данных дифференциальным уравнением системы кривых Пирсона (таблица
2).
Литература:
1. Колтунова, А.И. Некоторые закономерности текущего накопления фитомассы в
древостоях / А. И. Колтунова //
Леса Урала и хозяйство в них. –2004. – Вып. 24. – С.148–157.
2.
Кремер, Н. Ш.
Эконометрика : учебник для вузов / Н. Ш. Кремер, Б. А. Путко; под ред. проф. Н.Ш. Кремера. – Москва: ЮНИТИ-ДАНА, 2002. – 311 с.
3. Усольцев, В. А. Фитомасса лесов Северной Евразии: нормативы и элементы
географии / В. А. Усольцев. –Екатеринбург: УрО РАН, 2002. – 762 с.
4. Усольцев, В. А. Биологическая продуктивность лесов Северной Евпазии:
методы, база данных и её приложения/ В. А. Усольцев. – Екатеринбург: УрО РАН,
2007. – 636 с.
5. Швиденко, А.З. Таблицы и модели хода роста и продуктивности
насаждений основных лесообразующих пород Северной Евразии:
нормативно-справочные материалы / А.З.
Швиденко, Д.Г. Щепащенко, С. Нильссон,
Ю.И. Булуй. - Издание 2-е, доп. — М.:
Федеральное агентство лесного хозяйства, 2008. – 886 с.