Математика/1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Бахтина Ж.И.

ФГБОУ ВПО «Воронежский Государственный университет», Россия

О теории динамических уравнений на временных шкалах

В настоящей работе говорится о связи теории динамических уравнений на временных шкалах (далее – [ДУВШ]) с вариационным исчислением. Некоторые вопросы указанной теории были затронуты ранее в [6].

[ДУВШ] получила развитие в основном в работах англоязычных авторов (см. [2]-[4]). Актуальность своей тематики они мотивируют самыми разнообразными приложениями и интерпретациями в области космологии, в области пульсирующих и эпизодически замирающих процессов в биологии и экономике.

Начиная с работ Стефана Хилгера в 1988 г., [ДУВШ] претендует на своеобразное направление в теории дифференциальных уравнений. В ней изучаются функции, аргументами которых являются точки временных шкал, а временной шкалой называется любое замкнутое подмножество из . Для временной шкалы в [ДУВШ] рассматривается динамическое уравнение вида

(1)

где под -производной функции понимается

(2)

Здесь Прокомментируем уравнение (1).

В (1) во втором слагаемом слева аргумент неизвестной функции подразумевает присутствие в уравнении феномена опережения. Ранее в работах Покорного Ю.В., Бахтиной Ж.И. было введено понятие дырки шкалы . Дополнение шкалы до всей числовой оси - открытое множество в силу замкнутости и поэтому состоит из объединения конечного или счетного числа интервалов. Именно каждый такой интервал был назван дыркой шкалы .

Как было выявлено ранее, теория [ДУВШ] со стороны математических традиционных концепций не полна: не предусмотрен анализ вопросов о существовании решений, об их зависимости от параметров, не обсуждаются вопросы полноты соответствующих функциональных пространств, где ищется решение, не обсуждаются привычные для обыкновенных дифференциальных уравнений качественные свойства решений типа теорем сравнения Штурма и т.д. Устремленность к главному вопросу теории [ДУВШ] - асимптотике решений при - достигается построением аппарата, где даже процедура интегрирования иррациональна. Поэтому основные результаты этой науки вызывают сильные сомнения. Тем более что результаты относятся к весьма узкому классу вопросов, и только в окрестности бесконечности. Надо сказать, что все же Покорным Ю.В. и Бахтиной Ж.И. было показано, что на основные объекты теории [ДУВШ] возможен корректный математический взгляд с позиции теории интеграла и меры, снимающий проблему разумного дифференцирования, невзирая на «дырявость» шкалы, и позволяющий строить и изучать некоторый аналог уравнения (1) в классе абсолютно непрерывных функций без всяких дырок в области определения аргумента.

Следует заметить, что мы были вынуждены определенные на временной шкале решения, а вместе с тем - и уравнение (1), непрерывно продолжать в дырках.

Пусть - множество левых краев дырок шкалы . Динамическое уравнение отличается от обыкновенного дифференциального только на множестве - это следует из определения -производных и функции . В теории [ДУВШ] предполагается, как правило, непрерывность коэффициентов и и непрерывность решений уравнения (1) вместе с производными и . Эти условия мы назвали допустимыми условиями [ДУВШ]. Далее заменим на более привычную запись . Нами была доказана следующая теорема.

Теорема. Пусть для уравнения (1) выполняются допустимые условия [ДУВШ]. Тогда существуют функции с локально ограниченным изменением на и такие, что каждому из допустимых решений u(x) исходного уравнения (1) (не забудем о смене обозначений) соответствует определенное и непрерывное на всем из решение уравнения

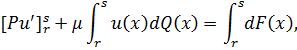
совпадающее с на шкале . Здесь интегралы понимаются по Стилтьесу.

Подобные интегро-дифференциальные уравнения хорошо известны. Они получаются путем исследования на минимум функционала потенциальной энергии соответствующей физической системы. В качестве таких систем могут выступать системы струн, стержней и т.д. Оказалось, что и эпизодически замирающие процессы в биологии тоже можно описать интегро-дифференциальным уравнением, указанным выше. А те условия, которые приводят англоязычные авторы на краях дырок как раз аналогичны тем, что получаем мы в процессе минимизации функционала потенциальной энергии следующей системы: две струны закреплены, например, на концах; правый конец левой струны соединен упругой связью с левым концом правой струны; левый конец правой струны упруго связан с внешней средой. Это своеобразная интерпретация развития биологической популяции в течении какого-то времени с присутствием одного периода спячки (одна «дырка» на временной шкале). В нашем примере образ биологического процесса – струна, период спячки – промежуток между струнами. Кроме того, видно, что система получилась непрерывной.

Таким образом, с помощью вариационного исчисления, теории меры, теории интеграла удается изучать, например, теорию динамических уравнений на временных шкалах.

Литература:

1. Покорный Ю.В. Осцилляционная теория Штурма-Лиувилля для импульсных задач/ Ю.В.Покорный, М.Б.Зверева, С.А.Шабров// Успехи математических наук, 2008. том 63, вып. 1 (379). С. 111-154.

2. Saker S.H. Oscillation of Second-Order Forced Nonlinear Dynamic Equations on Time Scales/ S.H. Saker// Electronic Journal of Qualitative Theory of Differential Equations 2005, No. 23, 1-17; С.57-64.

3. Hilger S. Analysis on measure chains - a unified approach to continuous and discrete calculus/ S.Hilger// Results Math. 18 (1990) 18-56.

4. Bohner M. Dynamic Equations on Time Scales/ M.Bohner, A.Peterson// An Introduction with Applications. Birkh user Boston, MA, 2001.

5. Сакс С. , Теория интеграла/ С. Сакс// М.: ИЛ, 1949; пер. с польск.: S. Saks, Theory of the integral, 2, revised edit., G. E. Stechert Co. VI, New York, 1937.

6. Бахтина Ж.И. О дифференциалах Стилтьеса на временных шкалах/ Ж.И.Бахтина// Саратов: Известия Саратовского университета, 2009. Т. 9. Сер. Математика. Механика. Информатика. Вып. 2. С. 3-5.