ДУАЛЬНЫЙ
ОПЕРАТОР И ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ПОГРАНИЧНОЙ ФУНКЦИИ[1]
Нефедов
В.В., Филиппычев Д.С.
Московский государственный университет имени
М.В.Ломоносова,
факультет вычислительной математики и кибернетики,
кафедра автоматизации научных
исследований
1. Введение. В работе [1] было рассмотрено применение
асимптотического метода пограничных функций (АМПФ) [2] к интегро-дифференциальному
уравнению плазма-слой [3], описывающему поведение электростатического
потенциала 
, как в основном объеме плазмы, так и в узком пристеночном
слое. Здесь безразмерные величины 
и 
соответствуют
потенциалу и линейной координате. Уравнение плазма-слой является
сингулярно-возмущенным, поскольку перед старшей (второй) производной стоит
малый параметр 
(
, где 
- дебаевская длина, 
- длина системы; 
). В пределе 
интегро-дифференциальное
уравнение переходит в интегральное уравнение, которое описывает поведение
потенциала только в основном объеме плазмы и носит название плазменное уравнение. Уравнение,
описывающее поведение пограничной функции нулевого порядка (первого члена
сингулярной части разложения АМПФ 
, в дальнейшем просто «пограничной функции») [1] является
дифференциальным уравнением второго порядка. При этом, пограничная функция
описывает основное падение потенциала вблизи стенки 
.
Численное решение уравнения плазма слой
было получено в работах [3,4]. Сингулярный характер уравнения плазма-слой
приводит к возникновению узкой области с большим изменением решения
(пограничный слой). Расчеты с 
[4] показали резкое
изменение 
непосредственно
вблизи стенки (
) и довольно гладкое уменьшение немного далее от границы (
). Такое быстрое изменение решения вблизи стенки приводит к
трудностям численного решения уравнения пограничной функции вблизи стенки:
плохо вычисляются градиенты функции, не хватает разрядности представления
чисел. Такое изменение приводит к быстрому накоплению ошибок вычислений в
пошаговых схемах расчетов (например, в простейшей схеме бегущего счета, когда
для второй производной используется трех точечный шаблон). В связи с этим
желательно получить аналитическое выражение, приближенно описывающее поведение
пограничной функции.
2. Асимптотический метод пограничных функций. Одним из эффективных асимптотических методов теории
сингулярных возмущений является АМПФ [2]. В этом методе решение 
представляется в виде
двух степенных по 
рядов - регулярного 
и пограничного 
:
, 
, (1)
, (2)
(3)
Коэффициенты рядов (2), (3) определяются в результате
формальной подстановки разложения (1) в рассматриваемое уравнение. Коэффициенты
ряда (3) экспоненциально
стремятся к нулю с ростом 
(
, 
) и называются пограничными
функциями.
Правая часть уравнения также
представляется в виде суммы регулярной 
и пограничной 
частей. После
подстановки (1) в правую часть 
становится функцией и
. Приравнивая коэффициенты при одинаковых степенях 
(раздельно для
функций, зависящих от 
и 
) получаем уравнения для определения неизвестных функций 
и 
:
(4)
. (5)
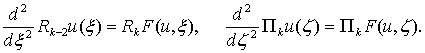
Первое соотношение (4) представляет собой вырожденное
уравнение АМПФ уравнения плазма-слой и является уравнением плазменного приближения.
3. Уравнение плазменного приближения. Если в уравнении плазма-слой [3] положить формально 
, то получается, так называемое, плазменное приближение, которое справедливо только в области вне
пристеночного слоя:
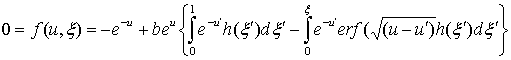. (6)
Здесь 
- функция источника.
В дальнейшем плазменное приближение будет
обозначаться как 
. Для уравнения (6) ставится только одно краевое условие 
.
Процедура получения решения интегрального
уравнения плазменного приближения (6)
подробно рассматривалась в работе [3]. Там же в неявном виде было получено
решение для произвольной функции источника 
: 
, 
- функция Доусона, а 
. Для выбранной формы функции источника 
решение принимает следующий
вид [3]: 
,
.
После интегрирования по всей области с
учетом нормировки [3] 
получается 
, в котором величина 
соответствует
значению решения плазменного уравнения
(6) на входе в слой 
. В работе [3] для нахождения 
было выведено трансцендентное уравнение, решение которого
можно получить только численными методами. После нахождения 
вычисляется параметр 
и, следовательно, 
. При значениях 
решение представляет
собой “полочку” постоянной величины 
[3,4].
4. Уравнение пограничной
функции. Поведение
пограничной функции описывается уравнением [1]:
, (7)
здесь 
, 
– растянутая
координата, 
. На пограничную функцию накладываются два дополнительных
условия. Одно из этих условий задается падением потенциала на стенке 
: 
[3,4].
Поскольку 
, то первое условие преобразуется к виду 
. Вторым условием является поведение пограничной функции на
бесконечности 
. Задача плазма-слой решалась [3,4] в области 
. В данной работе рассматривается в основном узкая область
вблизи стенки (
, при
), в которой 
.
5. Метод дуального
оператора.
В разделе рассматривается нелинейное уравнение общего вида: 
, где 
- вектор параметров,
появляющийся при математическом описании физической задачи. Дуальный оператор
[5] является аналогом сопряженного оператора линейной теории. Для его
формирования необходимо существование производной Гато для оператора 
: 
. Дуальный оператор 
определяется
равенством:
. Здесь скобки 
и 
обозначают скалярные
произведения, соответственно, в исходном и дуальном пространстве, а фигурная скобка
- бинарную форму
граничных (начальных и/или краевых) условий, получающуюся в результате
интегрирования.
В методе
дуального оператора формируются интегральные операторы: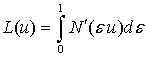 
и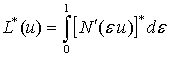 
. Эти интегральные операторы используются при записи
уравнений для запаздывающего пропагатора 
и опережающего
пропагатора 
, которые являются аналогами функции Грина линейной теории. В
дальнейшем будет использоваться только опережающий пропагатор 
, для нахождения, которого получается линейное уравнение
(8)
с соответствующими
граничными условиями. С помощью 
решение исходного
уравнения выписывается в следующем виде [5]:
(9)
Метод
дуального оператора снижает порядок дифференциального уравнения на два [5].
Рассматриваемое в этой работе дифференциальное уравнение второго порядка (7)
сводится к алгебраическому уравнению. Последнее обстоятельство позволяет
использовать этот метод для написания как трех точечных уравнений [6], так и
для получения асимптотических решений.
6. Применение метода дуального оператора
к уравнению пограничной функции.
В работе [6]
метод дуального оператора [5] использовался для нахождения приближенного
решения уравнения (7). Отметим некоторые моменты получения решения. Исходный
нелинейный оператор записывается в виде: 
, для дуального оператора получается 
, а уравнение пропагатора (8) принимает следующий вид:
(10)
(
). Коэффициент
является нелинейной
функцией 
.
Поэтому, в общем случае не удается получить решение уравнения (10) в
аналитическом виде. Однако в приближении 
уравнение (10)
становится уравнением с постоянным коэффициентом и имеет аналитическое решение,
с помощью которого соотношение (9), а также решение уравнения (7) принимает вид
(см. [6]):
(11)
. - начальная координата. Выберем для пропагатора однородные
краевые условия первого рода: 
. Тогда выражение для решения (11) упрощается за счет
устранения производной 
: 
. После замены 
получим окончательно
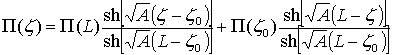. (12)
Если выполнено
условие 
(например, когда 
, или 
) то выражение (12) упрощается. В итоге приходим к решению,
для которого необходимо знать только краевое значение 
:
. (13)
Используя определение 
, асимптотику (13) можно переписать в виде:
. (14)
Следует
отметить, что соотношение (13) удовлетворяет граничным условиям: 
, 
. Таким образом, формула (13) является приближенным решением
рассматриваемой задачи. На правой границе 
. Поэтому асимптотика (14) также практически обращается в
нуль.
7. Результаты численных расчетов. Представим результаты
расчетов 
,
проведенных по формуле (13). Наблюдается монотонное возрастание погрешности.
Относительная ошибка меньше 
достигается в области
вблизи левой границы 
, а уровень 
.
Максимальная ошибка 
достигается на правой
границе области 
. В этих расчетах величина 
вычислялась на левой
границе области и равнялась 
. Представим еще относительные ошибки “полного” решения
задачи плазма-слой 
. На всей длине расчета погрешность укладывается почти в 
, 
, 
.
Поведение
пограничной функции первого порядка 
определяется
дифференциальным уравнением второго порядка (второе уравнение (5)). Помимо
всего прочего, пограничная функция входит в интегралы свободного (от 
) члена. Учитывая неудовлетворительные результаты расчетов,
приведенных с использованием пошаговых схем, нахождение значений пограничной
функции в области интегрирования (область источника; “дальняя” зона 
) становится весьма проблематичным. Остается в этой области
использовать только асимптотические решения (13) или (14).
Как указывалось
выше, при использовании формулы (13), в точности выполняются краевые условия на
обеих границах области расчета для полной задачи плазма-слой. Кроме того,
формулу (13) в совокупности с начальным (плазменным)
решением 
можно использовать
как хорошее начальное приближение для итерационного процесса нахождения решения
полной задачи плазма-слой [3,4]. Заметим, что значение падения потенциала на
стенке 
, полученное по оценочной формуле в работе [3], лишь на
немного меньше значения 
, полученного в результате численного решения задачи
плазма-слой при 
[3,4].
При оценке
результатов надо иметь в виду, что была рассмотрена только пограничная функция
нулевого порядка. Большим значениям относительной ошибки соответствуют
небольшие значения абсолютной ошибки. Такое отличие вполне может быть
обусловлено пограничной функцией первого порядка.
8.
Заключение.
Используя формализм метода дуального
оператора, в работе получено аналитическое решение уравнения пограничного слоя
(13). Построенное решение удовлетворяет краевым условиям задачи на обеих
границах области расчета полной задачи плазма-слой. Поэтому ее можно считать за
приближенное решение рассматриваемой задачи. За
использование (13) в качестве пограничной функции говорит следующее:
§
отсутствие эффекта накопления ошибок вычислений;
§
возможность вычисления значений в «дальней» области
источника для вычисления интегралов, которые входят в состав свободного члена
дифференциального уравнения пограничной функции первого порядка;
§
точные значения на обеих границах области расчета
полной задачи плазма-слой позволяют использовать пограничную функцию в сумме с
начальным (плазменным) приближением в качестве начального приближения этой
задачи.
СПИСОК ЛИТЕРАТУРЫ
1.
Филиппычев
Д.С. Метод пограничных функций для получения асимптотического решения уравнения
плазма-слой // Прикладная математика и информатика № 19: Сб. /Под ред. Д.П.
Костомарова, В.И.Дмитриева - М: MАКС Пресс, 2004 , С. 21-40.[2]
2.
Васильева
А.Б., Бутузов В.Ф. Асимптотические разложения решений сингулярно возмущенных
уравнений. - М.: Наука, 1973. 272 c.
3.
Emmert
G.A., Wieland R.M., Mense A.T., Davidson J.N. Electric sheath and presheath in
a collisionless, finite ion temperature plasma // Phys.Fluids. 1980. Vol. 23, N 4. P. 803-812.
4.
Филиппычев
Д.С. Численное моделирование уравнения плазма-слой // Вестн. Моск. ун-та.
Сер.15. Вычислительная математика и кибернетика. 2004. № 4. С. 32-39.
5.
Cacuci
D.G., Perez R.B., Protopopescu V. Duals and propagators: A canonical formalism
for nonlinear equations. // J.Math.Phys. 1988. Vol. 29. N 2. P.335-361.
6.
Филиппычев
Д.С. Применение формализма дуального оператора для получения пограничной
функции нулевого порядка уравнения плазма-слой // Прикладная математика и
информатика № 22: Сб. под ред. Д.П.Костомарова, В.И.Дмитриева - М: MАКС Пресс,
2005, С. 76-90.[3]