Математика/4. Прикладная математика

Д.ф.м.-н. Бурова И.Г.

Санкт-Петербургский государственный университет, Россия

О построении расчетных формул для решения задачи Коши с помощью интегро-дифференциальных сплайнов

Минимальные интерполяционные сплайны подробно изучались в работе [1]. Отличительная черта этих сплайнов ─ наличие интерполяционного бази-са, причем носители базисных функций занимают несколько сеточных интер-валов. Эти сплайны удобно применять для построения приближений функций и их производных с заданным порядком аппроксимации. Решение интерполяци-онной задачи Эрмита, Лагранжа и Эрмита-Биркгоффа получаем с помощью по-строения суммы произведений значений функции и/или ее производных в узлах сетки и соответствующих базисных функций. Интегро-дифференциальные по-линомиальные сплайны предложены в книге [4].

В этой работе построим численные методы для решения задачи Коши на основе полиномиальных и неполиномиальных интегро-дифференциальных сплайнов [2]. Некоторые расчетные формулы решения задачи Коши были представлены на международной конференции в Праге [3].

1. О построении неполиномиальных интегро-дифференциальных сплайнов. Пусть α, m, , , , n, , q ─ целые неотрицательные числа, ,, =+ , ─ сетка упорядо-ченных узлов, конечная или бесконечная, …< возможно В дальнейшем будем рассматривать сетку равноотстоящих узлов с шагом h.

Пусть ─ чебышёвская система на причем функции строго монотонны и отличны от нуля на . Для функции на промежутке построим приближение

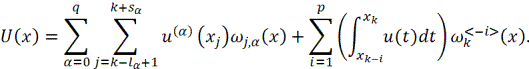
Базисные функции содержится в находим из условий:

Предположим, что определитель Вронского

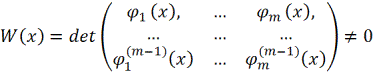
при Разлагая определитель

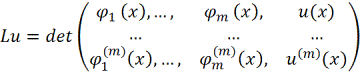
по элементам последнего столбца и деля все слагаемые на , приходим к выражению

Можно показать, что справедливо неравенство

Здесь и далее считаем, что

Рассмотрим частный случай. На промежутке базисные функции находим из системы уравнений

где

.

Переходя к переменной по правилу получаем

Графики базисных сплайнов представлены на рис.1.

251658240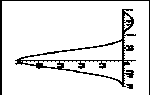251658240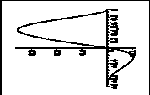251658240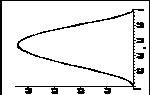

Рис.1. Графики базисных функций .

2. Построение расчетных формул для решения задачи Коши. Будем решать задачу Коши

С помощью формулы Ньютона-Лейбница

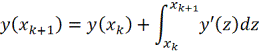
Нетрудно получить расчетную формулу для решения задачи Коши, заменяя

подынтегральное выражение на . Например, для рассматриваемого частного случая, получаем

3. Результаты счета

3.1. Рассмотрим численное решение предложенным численным методом задачи Коши

Нетрудно убедиться, что решение этой задачи имеет вид

График погрешности решения задачи Коши при равномерной сетке с шагом h=0.001 приведен на рис. 2 ( – приближенное решение).

251658240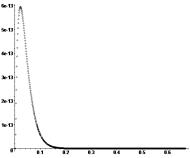251658240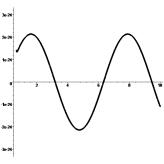

Рис.2. График погрешности численного решения задачи Коши

На рис.3. приведен график погрешности численного решения задачи Коши

Точное решение этой задачи y=sin(x).

251658240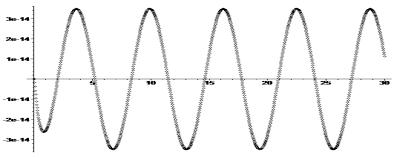

Рис.3. График погрешности при равномерной сетке с шагом h=0.01.

Литература

1. Бурова И.Г. Демьянович Ю.К. Теория миниимальных сплайнов. СПб. 2010. 364 c.

2. Бурова И.Г. О моделировании неполиномиальных интегро-дифференциаль-ных приближений / / Труды СПИИРАН. Вып. 4 (19). 2010. С.176-202.

3. Бурова И.Г. Materialy IX mezinarodni vedecko-prakticka konference «Moderni vymozenosti vedy-2013». 27.01.13-05.02.2013. Прага. 2013. С. 3-6.

4. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М. 2008. 480 c.