ПОКАЗАТЕЛИ ДЛЯ ОЦЕНКИ ДОЛГОВЕЧНОСТИ
ЗНАНИЙ УМЕНИЙ И НАВЫКОВ
Л.Г. Поляков, Е.М. Тишина,
Г.С. Слюсар
Пензенский государственный университет архитектуры и строительства г.Пенза
кафедра "Начертательная геометрия и графика"
Формирование высококвалифицированных
специалистов неразрывно связано с качеством их профессиональной подготовки, а
следовательно и с надежностью обучения. Одними из составляющих свойств
надежности обучения является долговечность применения полученных знаний, умений
и навыков на практике.
По аналогии определений составляющих
надежности, применяемых для технических систем [1,2,3,4], но адоптированных к
процессу обучения, понятия долговечность будут иметь следующий вид [5].
Долговечность это свойство системы обучения сохранять субъектами (обучаемыми)
полученные знания, умений и навыков в пределах заданного уровня от начала их
приобретения до наступления предельного состояния (т.е. полной утраты знаний)
или необходимого (заданного) срока, при установленной системе поддержания
необходимого уровня знаний, умений и навыков и восстановления их при утрате.
На практике, решение любой задачи, в общем
случае, представляет собой последовательность выполнение отдельных операций
(шагов). Шаг решения задачи - это применение конкретной формулы, отдельной
операции, использования отдельного умения или навыка, принятие промежуточного
решения по принципу «да – нет» и т.п. Говоря другими словами, это элементарное
действие или этап в процессе решения задачи.
Если принять, что отдельная операция это
элемент решения задачи, а саму последовательность решения задачи как взаимосвязь
этих элементов, то процесс решения задачи в целом можно представить в виде
системы взаимосвязанных элементов.
Учитывая, определения элемент и система,
то показатели долговечности можно подразделять на показатели элементов и
показатели систем знаний, умений и навыков.
Для дальнейших рассуждений введем понятия
«Работоспособное состояние» и «Состояние отказа» элемента и системы. Если под
работоспособным состоянием элемента или системы понимать такое состояние уровня
знаний, умений и навыков испытуемого, при котором он может достичь
положительного результата решения, то не возможность получения положительного
решения будет являться состоянием отказа элемента или системы.
В данной статье рассматриваются показатели
долговечности, используемые в технике [1,2,3,5], но адоптированные к процессу
обучения.
Показатели долговечности знаний,
умений и навыков
Из определения долговечности видно, что
она характеризует сохранение уровня полученных знаний, умений и навыков от
начала их получения до полной утраты их. При этом, промежуток времени может
прерываться на восстановление утраченных знаний, умений и навыков. В отличие от
свойства безотказности [4], которое характеризует непрерывность сохранения
знаний, умений и навыков за определенный промежуток времени, независимо от
того, когда и где берется этот промежуток, долговечность тоже характеризует
сохранение знаний, умений и навыков, но промежуток времени здесь строго определен.
Долговечность каждого элемента или системы
характеризуется сроком безотказного применения знаний. Это означает, что после
приобретения определенного уровня знаний, умений или навыков они не утратятся в
течении каково-то промежутка времени Тр
(величину Тр в последующим будем называть сроком службы
элемента).
Срок службы элемента (Тр,i) – это календарная продолжительность использования элементарного знания,
умения или навыка одного i-го испытуемого от начала его приобретения до
наступления предельного состояния, т.е. до состояния отказа.
На рис. 1 показана графическая
интерпретация формирования срока безотказного применения i-тых
элементов системы знаний, умений и навыков. Из рис. 1 видно, что величина
продолжительности срока безотказного применения знаний, умений и навыков в
значительной степени зависит от допуска (
) задаваемого уровня знаний, умений и навыков
определяемого по формуле
, (1)
где хпр – предельное значение
параметра уровня знаний, умений и навыков до которого допускается его уменьшение;
х0,i
– начальное значение параметра уровня знаний, умений и навыков i-го
элемента.
Срок службы элемента, как и любая
случайная величина, характеризуется законом распределения, в частности,
плотностью распределения ресурса f(Tp),
показанной на рис. 1.
Для оценки совокупности испытуемых для
отдельного элемента знаний, умений и навыков существуют специальные показатели
долговечности – средний срок службы элемента (Тр,ср) и гамма-процентный срок службы элемента (
).
Средний
срок службы (Тр,ср)
– это математическое ожидание календарной продолжительности использования элемента
знаний, умений и навыков для совокупности испытуемых от начала его приобретения
до наступления предельного состояния, т.е. полной утраты элемента знаний,
умений или навыков.
Гамма-процентный срок службы элемента (
) – эта величина
срока службы элемента, при которой обеспечивается вероятность безотказности полученных
знаний р(
), равной значению 
, выраженному в
процентах.
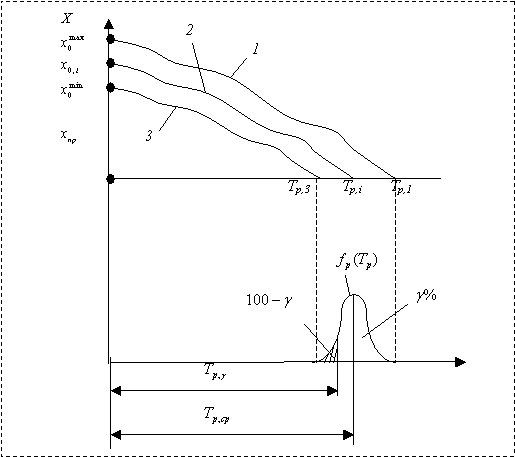
Рис. 1. Графическая интерпретация
формирования срока службы:
1-го испытуемого – Тр,1; 2-го испытуемого – Тр,2; 3-го испытуемого – Тр,3; среднего срока службы
элемента – Тр,ср;
гамма-процентного срока службы элемента – 
Величина 
назначается или
выбирается (90; 95; 99; 99,9%). Гамма-процентный срок службы элемента
определяется так же, как 
календарным временем.
Показатели долговечности для систем
знаний, умений и навыков
Как говорилось выше, решение задач это
есть взаимодействие (соединение) элементов влияющих на результат решения.
Количество элементов, входящих в соединение и их способ соединения при решении
конкретной задачи или совокупности задач будем считать системой.
Исходя из теории вероятностей, различают
три основных способа соединения элементов в системах [6]: последовательное
(основное); параллельное (кроме основного включает избыточные элементы); смешанное
соединение, т.е. часть элементов соединены последовательно, а часть
параллельно.
По сравнению с расчетом показателей
безотказности системы знаний, умений и навыков для показателей долговечности и
безотказности системы используется принцип выбора максимального или минимального
численного значения этих показателе рассчитанных для элементов.
Последовательное соединения элементов (рис.2).
Рис. 2. Последовательное
соединение элементов системы
Для такой системы значения показателей
должно выбирается как
, (2)
где 
- параметр системы
применительно к конкретному свойству надежности k-го назначения параметра (здесь k означает:
средний срок службы системы знаний, умений и навыков; гамма-процентный срок службы
системы знаний умений и навыков; средний срок хранения системы знаний, умений и
навыков);
- значения параметров
множества элементов (от 1 до N), входящих в систему j-го показателя по его назначению (здесь j
означает: средний срок службы элемента; гамма-процентный
срок службы элемента);
- минимальное численное значение параметра j-го
назначения из совокупности элементов 
;
N - число элементов в системе.
Параллельное соединение элементов (рис. 3.). Для такой системы значения показателей
должно выбирается как
, (3)
где 
- максимальное
численное значение параметра j-го назначения из совокупности элементов 
.
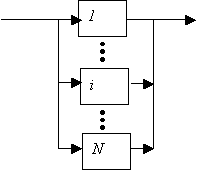
Рис. 3. Параллельное
соединения элементов
Смешанное соединение элементов. При таком соединении существуют два случая: случай
(а) – последовательно-параллельное; случай (б) – параллельно-последователное.
На рис.4 приведены упрощенные схемы таких соединений.
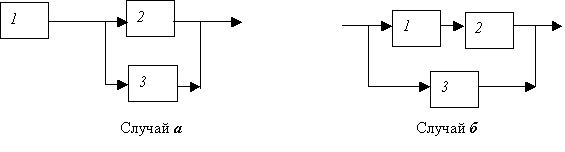
Рис. 4. Смешанное
соединение элементов
Для таких случаев
систему упрощают путем последовательного объединения элементов, приводя их в
конечном случае к виду рис.2 или рис.3. Например, система рис.4 (случай а) приводится к виду рис.2, а система
рис.4(случай б) – к виду рис.3.
Если система имеет
наиболее сложную схему соединений элементов, то в этом случае схему постепенно
упрощают, расчленяя ее на элементарные подсистемы (рис.2, 3, 4) и используя
зависимости (2), (3) приводят промежуточные и окончательный расчеты численных
значений показателей.
Таким образом, если под элементами системы
понимать отдельные дисциплины, разделы, параграфы и их составляющие, то
появляется возможность количественной оценки показателей долговечности получаемых
знаний, умений и навыков при подготовки специалистов. Кроме того, количественно
оценивая составляющие надежности можно управлять процессом подготовки специалистов
и строить прогнозирующие модели эффективности использования их уровня знаний,
умений и навыков.
Список литературы
1. ГОСТ 27.002-89. Надежность в технике.
Термины и определения.
2. Обслуживание и ремонт авиационной
техники по состоянию /Н.Н. Смирнов, А.А. Ицкович. – М.: Транспорт, 1987
3. Справочник по расчету надежности машин
на стадии проектирования /Б.Ф. Хазов, Б.А. Дедусев. -. М.: Машиностроение,
1986.
4. К вопросу о безотказности использования
полученных знаний / Л.Г. Поляков, Е.Е. Петрикова – Пенза: ПГТА, 2010.
5. Показатели долговечности и
сохраняемости полученных знаний / Л.Г. Поляков - Пенза: ПГУАС, 2010.
6. Теоретические основы эксплуатации и
ремонта вооружения /В.Н. Чухнин, Н.Н. Вершинин. – Пенза: ПГУ, 2001.
