Тишина Е.М.

Старший преподаватель кафедры «Начертательная геометрия и графика» Пензенского университета архитектуры и строительства

ИСПОЛЬЗОВАНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ПРОЦЕССА ОБУЧЕНИЯ

Для повышения эффективности процесса обучения необходимо проведение современных научных исследований опирающихся на использование методов математического моделирования. С этой целью была разработана математическая модель учебного процесса.

Математическая модель реализована в виде дискретной геометрической конструкции в пятимерном пространстве. Для построения математической модели учебного процесса использовалась многомерная геометрия и в частности, метод предельного геометрического моделирования. Процесс обучения представляется как поверхность в многомерном пространстве. С размерностью равной сумме параметров входа и выхода. В нашем случае, размерность предельного пространства равна пяти (четыре параметра входа и один параметр выхода)[1].

Выделенные параметры имеют значительный диапазон изменений, анализ которого технически сложен. И по этой причине был ограничен до трех вариантов: ниже, норма и выше. Норма определяется исходя из образовательного стандарта. В результате вместо поверхности получим дискретную конструкцию. Которая будет служить математической моделью учебного процесса [1].

Исследование предложенной дискретной конструкции в пятимерном пространстве требуется проводить одновременно, но технические средства, соответствующие нашему восприятию пространства, не дают такой возможности. Следовательно, необходимо применение традиционного метода сечений, и в частности, использовать трехмерные сечения. Для выделения пяти уровней влияния обратной связи на процесс обучения. С целью сокращения вычислительных операций был применен математический аппарат многомерной геометрии, гарантирующий построение плоских вариантов четырехмерных сечений, позволяющих установить закономерность влияния уровней обратной связи на характеристики, определяющие эффективность процесса обучения.

Логическая структура математической модели учебного процесса представлена на рис.1.

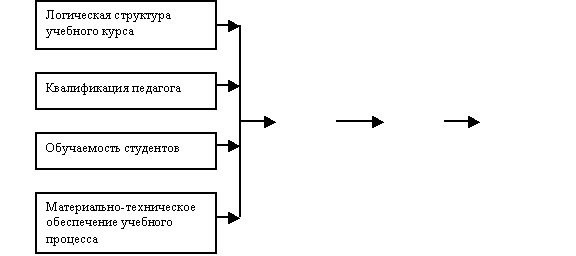
Рис. 1. Логическая структура математической модели учебного процесса

Для повышения качества знаний по графическим дисциплинам, создана оптимальная методика обучения, этапами которой является: а) анализ исходных параметров, учитывающий конкретные условия; б) определение уровня обратной связи, соответствующего рассматриваемой ситуации, с использованием разработанной математической модели; в) формирование оптимальных действий, направленных на повышение качества обучения, форм их реализации, на основе практического использования математической модели [2].

Реализация предложенной оптимальной методики обучения осуществляется посредствам следующих действий. Анализируется исходные параметры, с целью выявления их состояния, которое может соответствовать оптимальной, нормальной или критической ситуации. Используя данные, представленные в виде графов и таблиц, описывающих результаты подсчета суммарных числовых кодов точек различных типов, определяется уровень обратной связи, соответствующий анализируемой ситуации [2].

Согласно выявленному уровню обратной связи, формируется оптимальная методика обучения, подбираются виды ее реализации. Это возможно, с учетом информации, представленной в таблицах, характеризующих значимость исходных параметров. Оценивающих диапазон изменения данных, зависящий от различных уровней обратной связи и непрерывной шкалы суммарных числовых кодов. Подобный подход позволяет повысить эффективность процесса обучения методами математического моделирования, за счет использования соответствующих видов подачи информации, типов контроля качества знаний и коррекции [2]. Представление соответствующих схем, сечений, графов, таблиц и диапазонов изменений параметров из-за их сложности и большого объема вычислений в печатном издании не целесообразно.

Разработанная методика, подверглась экспериментальной проверке на примере изучения дисциплины «Черчение». Для этого выделялись контрольные и опытные группы. Результаты обработки статистических данных исследований показали, что предложенная методика обучения черчению позволяет доступными и эффективными способами повысить качество обучения посредствам воздействия на учебный процесс, за счет оптимального подбора варьируемых параметров, таких как, обучаемость студентов (Об), материально-техническое обеспечение учебного процесса (Мо), квалификация педагога (Кв), логическая структура дисциплины «Черчение» (Лс).

Например, выбираем конкретные значения параметров: обучаемость студентов, материально-техническое обеспечение учебного процесса, квалификация педагога. Эти данные берутся на основе проведенного исследования, в котором выделялись восемнадцать групп студентов (общей численностью 450 человек) строительного, технологического, автомобильно-дорожного институтов. Девять групп (ПГС – 11,12,14; ЭУН – 11,12; ГСХ – 11,12; ССК-11, ПСМ-11) были контрольными, а остальные (ОБД – 11,12; ААХ – 11,12; АДА – 11,12; ИЗО – 11,12; АФО – 11) – экспериментальными. В качестве логической структуры используется предложенная структура дисциплины «Черчение».

Следующим этапом является нахождение уровня обратной связи, с помощью математической модели [1].

Так, для контрольных групп: обучаемость студентов (Об) – норма и выше; материально-техническое обеспечение учебного процесса (Мо) – норма; квалификация педагога (Кв) – норма; логическая структура дисциплины «Черчение» (Лс) – норма. Следовательно, итоговый уровень обратной связи соответствует трем, а суммарный числовой код – 13,5. Из этого следует – Кв2, Мо2, Об2, Лс2, где цифры указывают уровень параметра (1, 2, 3 – соответственно, ниже, норма и выше).

Для экспериментальных групп: обучаемость студентов (Об) – норма и ниже; материально-техническое обеспечение учебного процесса (Мо) – норма; квалификация педагога (Кв) – норма; логическая структура дисциплины «Черчение» (Лс) – норма. Следовательно, итоговый уровень обратной связи соответствует четырем, а суммарный числовой код – 20,2. Из этого следует – Кв1, Мо1, Об2, Лс1.

Анализируя данные полученные, с использованием предложенной модели, осуществляем корректировку методики обучения, которая приведет к оптимизации результата. Для рассматриваемого случая, у экспериментальных групп необходимо воздействовать на показатели Кв, Мо, Лс, в сторону их увеличения. Это позволит при фиксированном значении Об повысить качество обучения студентов.

Подобный подход, использующий разработанную оптимальную методику обучения и методику изучения «Черчения», позволяет повышать качество проведения учебного процесса, что приведет к росту знаний студентов.

Таким образом, увеличение эффективности процесса обучения методами математического моделирования обеспечивается посредством аналитических исследований совокупности характеристик: обучаемость студентов; квалификация педагога; материально-техническое обеспечение учебного процесса; логическая структура учебного курса и категории «Обратная связь», приводящих к созданию математической модели, реализованной в виде дискретной геометрической конструкции в пятимерном пространстве. Построенные плоские варианты четырехмерных сечений позволяют установить взаимовлияние уровней обратной связи и параметров, определяющих эффективность процесса обучения, с учетом количественной оценки их статуса.

Оптимизация процесса обучения графическим дисциплинам осуществлена за счет применения предложенной методики обучения «Черчению», реализованной и экспериментально исследованной на примере, контрольных и опытных групп. Учитывались логическая структура дисциплины, архитектура элементов, декомпозиция дидактических блоков и единиц, содержание тематических модулей и составляющих их разделов.

Перспективы дальнейших исследований заключаются в целесообразности анализа возможности применения созданной оптимальной методики, в качестве основы для разработки универсальных, адаптивных и эффективных методов и форм обучения, а также, разработки методик обучения другим дисциплинам графического блока.

ЛИТЕРАТУРА

1. Найниш, Л.А. Многоменая конструкция – математическая модель учебного процесса [Текст] / Л.А. Найниш, В.С. Горбунова, Е.М. Тишина, Н.А. Филиппова // Профессиональная подготовка учительства: История, теория, практика: труды всерос. науч-практ. конф. – Пенза: ПГПУ, 2006. – С. 293-298.

2. Найниш, Л.А. К вопросу проектирования оптимальной обучающей технологии [Текст] / Л.А. Найниш, В.С. Горбунова, О.Н. Кузнецова, Е.М. Тишина, Н.А. Филипова// Профессиональное образование: проблемы и перспективы развития: труды межд. науч.-прак. кон. – Пенза: ПГТА, 2005.- С. 35-39.