Физика/1. Теоретическая физика
К.ф-м.н. Галиахметов А.М., Щербань Р.А.
Донецкий национальный технический
университет, Украина
Анизотропная космологическая модель
в теории Эйнштейна – Картана
Наблюдаемая
крупномасштабная изотропия современной Вселенной не гарантирует изотропию ее
ранних стадий эволюции. Хорошо известно [1, 2], что проблема описания ранней
Вселенной допускает сценарий анизотропного расширения.
В рамках
программы построения калибровочной теории гравитационных взаимодействий большую
актуальность имеет Пуанкаре калибровочная теория гравитации и, в частности, ее
простейший вариант – теория Эйнштейна – Картана (ТЭК). Эта теория является
расширением общей теории относи- тельности (ОТО) на пространство – время с
кручением и она сводится к ОТО, когда кручение исчезает.
В
последнее время интерес к ТЭК возрос в связи с тем, что кручение естественно
возникает в супергравитации [3, 4], теориях Калуцы-Клейна [5, 6] и суперструн
[7, 8].
Первые
точные космологические модели в ТЭК со спинирующей жид- костью Вейссенхоффа в
качестве источника кручения были найдены для космологических моделей типа I [9]
и типов I и V [10] по Бианки.
Точные
космологические решения уравнений Эйнштейна-Картана для спинирующей жидкости
Вейссенхоффа и магнитного поля были получены для модели типа I по Бианки [11] и
для модели Кантовского-Сакса [12].
Точные
решения в пространстве-времени Римана-Картана для моделей типа I по Бианки,
содержащими жидкость Вейссенхоффа и космологическую константу, были получены в
работе [13].
Точные
общие решения уравнений Эйнштейна-Картана для анизот- ропных космологических
моделей типа I по Бианки с неминимально связанным скалярным полем были получены
и исследованы в работе [14].
В данной работе рассматриваются
однородные анизотропные космоло- гические модели с неминимально связанным духовым
(ghost) скалярным полем с
нелинейным потенциалом, ультрарелятивистским газом и жидкостью с предельно
жестким уравнением состояния.
Причины рассматривать духовое скалярное поле Ф
заключаются в сле- дующем: это поле выступает в качестве возможного кандидата
для описания темной материи [15] и темной энергии [16]; оно используется для
построения регулярных фантомных черных дыр [17].
Лагранжиан
модели выбираем в виде [18]:
. (1)
Здесь 
– скалярная кривизна связности 
; 
– символы Кристоффеля 2-го рода; 
– тензор кручения; 
– гравитационная постоянная Эйнштейна, 
и 
- лагранжианы ультра-
релятивистского газа и жидкости.
Отметим, что уравнение скалярного поля,
соответствующее лагранжиану (1), в отсутствие кручения при 
и 
будет
конформно-инвариантным.
Варьируя действие с лагранжианом (1) по
получим
, (2)
, (3)
, (4)
где
, (5)
, (6)
, (7)
(8)
Здесь и 
– оператор Д'Аламбера и ковариантная производная в римановом
пространстве, 
; 
; 
, 
и 
, 
- плотность энергии и давление ультрарелятивистского газа и
жидкости с предельно жестким уравнением состояния, соответственно.
В метрике однородной анизотропной
модели типа I по Бианки
(9)
Уравнение (2) и (4) с
учетом (3) приводится к виду
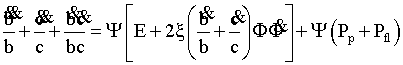, (10)
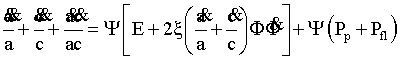, (11)
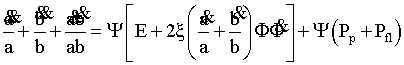, (12)
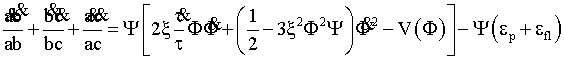, (13)
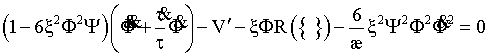, (14)
где 
, и
,
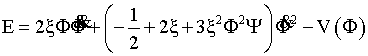(15)
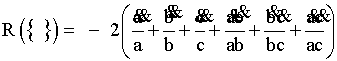. (16)
Для
ультрарелятивистского газа в метрике (9) справедливо
, 
. (17)
Для
жидкости с предельно жестким уравнением состояния выполняется соотношение:
, 
. (18)
Потенциал скалярного поля возьмем в
виде
, 
. (19)
Для 
, 
получено точное
решение:
, 
,
, 
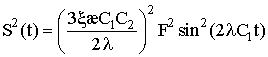, (20)
где 
, 
, 
и
, 
, 
,
, 
, 
,
, 
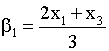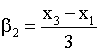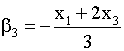, (21)
где 
, 
, 
, 
- постоянные
интегрирования; 
- квадрат следа
кручения 
; 
; 
.
Нетрудно видеть, что решение (20)
описывает реколлапсирующие модели с асимптотиками:
, 
,
, 
, (22)
где 
, 
.
Для максимума объемного фактора 
справедливо
; 
; 
. (23)
Литература:
1.
Misner C.W. // Astrophys. J. – 1968. – v. 151. –
P. 431.
2.
Зельдович Я.Б., Новиков
И.Д. Структура и эволюция вселенной. – М.: Наука, 1975.
3. Vandyck M.A.J. //
Class. Quantum Grav. – 1987. –v. 4. – P. 683.
4. Odintsov S.D. // Europhys.
Lett. – 1989. –v. 8. – P. 309.
5. Kalinowski M.W. //
Acta phys. austr. – 1981. –v. 23. – P. 641.
6. German G. // Class.
Quantum Grav. – 1982. –v. 2. – P. 455.
7. Kuusk P. // Gen.
Relativ. Gravit. – 1989. – v. 21. – P. 185.
8. Baker W.M. //
Class. Quantum Grav. – 1990. –v. 7. – P. 717.
9. Kopczyński W.
// Phys. Lett. A. –1973. –v. 43.– P.63.
10. Tafel J. // Phys. Lett. A. –1973.
–v. 45.– P.341.
11. Raychaudhuri A.K. // Phys.
Rev. D. – 1975. – v. 12. – P. 952.
12. Lorenz D. // J. Phys. A. – 1982.
– v. 15. – P. 2809.
13. Галицкий В.С., Пономарев В.Н. // Изв. вузов. Физика. –
1987, – № 3. – С. 116.
14. Galiakhmetov A.M. //
Grav. Cosmol. – 2007. – v.13. – P. 217.
15. Krause A., Ng S.-P. // Int. J.
Mod. Phys. A. – 2004. – v. 21. – P. 1091.
16. Holdom B. // JHEP – 2004. – v.
0407. – 063.
17. Bronnikov K. A., Fabris J. C.
// Phys. Rev. Lett. – 2006. – v. 96. – P. – 251101.
18. Galiakhmetov A. M. // Int. J.
Mod. Phys. D. – 2012. –v. 21. – 1250001.