INTERSUBBAND
MAGNETO- ABSORPTION IN SEMICONDUCTOR SUPERLATTICES.
G.B. IBRAGIMOV, R. G. ABASZADE, R.Z. IBAYEVA
Institute of Physics, Azerbaijan National Academy of Sciences, Javid av.
33, Az 1143, Baku, Azerbaijan
Artificial
semiconductor heterostructures after opportunities to custom design systems
with properties not encountered in natural materials. For example, it is
possible to fabricate superlattices in which electrons and holes are spatially
separated in adjacent layers with different compositions.
Semiconductor superlattices are fascinating model system for electrons
in a periodic potential [1]. They have enabled researchers to observe
long-sought physical phenomena such as Wannier – Stark localization [2] and
Bloch oscillations [3]. The absorption of
a superlattice in perpendicular magnetic field has been measured by Maan
[4].
In quantum well
such so-called intersubband transitions have been extensively studied and have
found applications in infrared detectors (“quantum well infrared phodetectors”)
[5] and lasers (“quantum cascade lasers”) [6].
In Ref.7, we
studied the interband (between conduction band and valence band) optical
transition of semiconductor superlattices. In this paper, we will study the
intraband (intersubband in the conduction
band) optical transition in the semiconductor superlattices .
We consider a
system consisting of 
electrons in a
superlattice with a potential well U(z)
of period 
along the z direction
under the influence of longitudinal magnetic field 
. The one - electron Hamiltonian then is given by
(1)
where 
is the effective mass
of a conduction electron with electric
charge 
and Landau gauge 
is given by 
.
The electron energy
and electron wave function given by the eigenvalues of Eqs. (1) can be expressed by
(2)
(3)
where
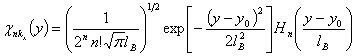
Where dimensions of the sample are assumed to be 
, 
being the miniband width and 
denoting the
periodicity of the potential, 
,
, 
is the 
th Hermite polynomial
and 
stands for the
tight-binding Bloch function in the z direction.
When a maqnetic field
is applied perpendicular to the superlattice, Landau quantization takes place
and the in-plane continuum splits up into discrete levels. At the same time,
the minibands , resulting from the motion of the electrons and holes in growth
direction, remain continuous.
For the case of non
– degenerate electron gas, in first order perturbation theory, the absorption
coefficient is given by [8, 9]
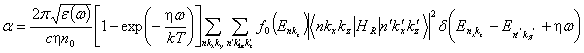(4)
We write Hamiltonian 
representing the
interaction with the high-frequency field in the form
(5)
where 
is the polarization
vector of the radiation field. In the calculation of the matrix elements of 
that follows, the
high-frequency field is assumed to be uniform.
A straightforward calculation of the square of
the matrix element in the representation (3)
We also replaced summations with respect to 
and 
in 
by the following relation [10]
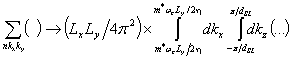
The electron distribution function 
for nondegenerate semiconductor superlattice in presence of
magnetic field, can be shown to be
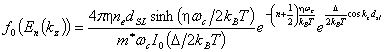
Here 
denotes the electron
density, and 
means the modified
Bessel function [11].
In order to obtain a smooth absorption
spectrum, we replace the 
function in a Eq.(4) with
a Lorentzian function with a half-width 
, viz.
The magnitude of 
is roughly equal to the energy spacing of the eigenstates.
Reference
1.H.T. Grahn (editor), Semiconductor Superlattices
(World Scientific, Singapore, 1995).
2.E.E. Mendez, F.Agullo-Runeda and J.M. Hong,
Phys.Rev.Lett. v.60,2426 (1988).
3.K.Leo,
Semicond.Sci. Technol.v.13, 249
(1998) and references theren.
4. J.C.Maan. Surf.Sci. v.196,538 (1988)
5.B.F. Levine, J.Appl.Phys. v.74, R1 (1993).
6.J.Fast, F. Capasso, D.L. Sivco, C.Sirtori,
A.L. Hutchinson and A.Y. Cho, Science v.264, 553 (1994).
7. M.I.Aliev, G.B. Ibragimov.,Transactions Azerbaijan
National Academy of Sciences, 2004, ¹2,
8.F.G. Bass and I.B.Levinson,
J.Exper.Theor.Phys. v.49,p.914 (1965)
9.G.B. Ibragimov, J.Phys. Stat.Sol.
(b),V.241,N8,p.1923-1927 (2004).
10. A.
Suzuki and M. Ogawa, J.Phys. C v.10, 1659 (1998).
11.
I.S. Gradshteyn and I.M. Ryzhik, Tables of Integrals, Series and Products
(Academic, New York,