УДК 536.24: 661.716.1

Физический смысл плёночной модели молекулы реагирующей в нано порах катализатора.

Игумнов В.С., Вавилов С.Н., Тепляков И.О., Гусева А.А., Лозина Е.Ю., Кубриков К.Г., Мамайкин Д.С., Виноградов Д.А.

Объединённый институт высоких температур РАН, Москва

Введение.

         В настоящее время известно три причины превращения молекул в другие соединения атомов. Это прямое столкновение молекул в системах: газ-газ, газ-жидкость, газ-твердое тело, жидкость-жидкость, жидкость- твёрдое тело и под воздействием лучистого потока (фотоны). Возможны также перестройки атомов внутри молекул в результате изменения во времени межатомных электромагнитных напряжений.  Будет рассматриваться элементарный акт химического превращения молекул происходящих при взаимных столкновениях во времени, т.е. кинетику химической реакции на молекулярном уровне. Это явление будет рассмотрено на примере взаимодействия водяного пара с метаном в результате чего образуется окись углерода и водород по формуле СН4 + Н2О = СО + Н2 (1) и молекулярный механизм этого химического превращения. Известно очень много работ по макрокинетике (формальной кинетике) реакции (1). Определение уравнения для определения скорости реакции заключающемся в эмпирическом получении константы скорости (метод Аррениуса, получение предэкспоненциального множителя k0 и энергии активации Е*) и подборки кинетической функции состоящей из концентраций реагирующих и образующихся веществ. Сразу следует отметить, что полученная формула подходит только для расчета и только для аппарата идентичного экспериментальной установки, на которой получено это выражение. Такое эффект происходит из-за сильного теплового потока требуемый для осуществления реакции (1). Для иллюстрации физического смысла плёночной модели молекулы реагирующей в нано порах катализатора взята именно названная реакция, т.к. её тепловой эффект (при нормальных условиях) сольно эндотермический и  составляет 206 кДж/моль (для сравнения для кипения воды требуется 41 кДж/моль). При составлении системы дифференциальных уравнений для расчета реального аппарата требуется точное определение стокового члена на проведения реакции (1), что будет показано ниже.

 

Постановка задачи.

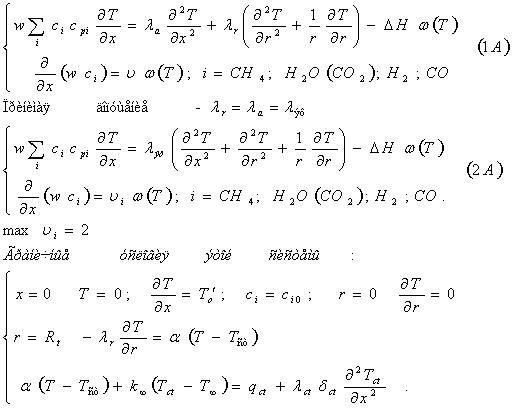         Для расчета размеров аппарата имеющего вид обогреваемой с наружи трубы, используется следующая система дифференциальных уравнений (А):

 

 

 

 

 

 

 

 

 

 

 

 

 

Где: w – скорость течения реагирующей смеси газов, ci – концентрация реагирующих газов, cpi – теплоёмкость реагирующих газов, Т , Tcт, Т∞– температура в слое катализатора стенки и окружающей среды, x – линейная координата в направлении течения газа,  λa , λr , λэф – теплопроводность аксиальная, радиальная, эффективная, ∆Н – тепловой эффект реакции,  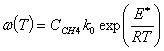- кинетическое уравнение, E* - Аррениусовская энергия активации, R = 8,314 – универсальная газовая постоянная α – коэффициент  теплоотдачи, R – внутренний радиус трубчатого реактора, δ – толщина стенки трубы, q – тепловой поток.

Трубчатый реактор заполнен катализатором никелевым катализатором в виде колец Рашига. Мы рассматриваем твёрдую поверхность передачи импульса (F dt = m dw) от поверхности нагрева внутри нано поры к отдельной молекуле газа. Поверхность нагрева это поверхность нано пор внутри катализатора. Средний диаметр поры 30 нм и внутренняя поверхность одной гранулы катализатора 65 м2. Поверхность катализатора в нано поре состоит в основном из Al2O3,  CaO, ZrO2 и Ni (восстановленного никеля). Считаем их вибраторами свойства, которых  определяются температурой слоя катализатора. С точки зрения квантовой механики  молекула представляет собой систему не из атомов, а из электронов и атомных ядер, взаимодействующих между собой. Внешние электроны, распределенные на поверхности, представляют собой сплошную оболочку. Форма оболочки зависит от расположения центра масс молекулы. Столкновения между молекулами газа и отдельных молекул с осцилляторами поверхности пор могут быть упругими, не полно упругими и не упругими.

Алгоритм структуры моделирования  плёночной модели реагирующих молекул.

          Для успешного решения системы уравнений А нам необходимо установить точное значения основных величин, которые все являются функцией температуры. В записанной системе А это эффективная теплопроводность λэф ,  ∆Н – тепловой эффект реакции и функция определения интенсивности стоков тепла в процессе химической реакции -  .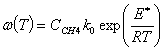

         Величина эффективной теплопроводности λэф и её функциональная зависимость от температуры с достаточной точностью определяется экспериментально. ∆Н – тепловой эффект реакции должен быть заменен на эффективный тепловой эффект ∆Нэф  полученный теоретически и подтвержденный экспериментальною [1,5,6].  

   (В)

Где  ∆Нэф - эффективный тепловой эффект, ∆Н – тепловой эффект реакции,  n – коэффициент избытка одного из компонентов реакции над стехиометрическим отношением (основной компонент Н2О), k0 -  коэффициент функционально зависящий от состава компонентов на входе в трубчатый реактор.

         Решение задачи замены определения скорости реакции  по  Аррениусу связана с использованием методов статистической физики и химии. Установим цепь молекулярных превращений в нано поре катализатора согласно известным моделям [2,3,4]. Для реакции (1) необходимо, что бы  молекула имела энергию 2,03эВ. Это соответствует температуре ТА= 36000К. Реакция (1) на катализаторе проходит при температуре 1100-1200К, поэтому согласно распределению Максвелла молекул с поступательной скоростью соответствующей  ТА очень мало, т.е. 10-7% . Поэтому происходит следующее: сначала происходит реакция разложения метана по формуле: СН4 → С + 2Н2 (2). В этой реакции энергия молекул для осуществления реакции (2) нужна 0.8 эВ.  Линейная скорость молекулы  соответствует ТБ = 14000К. Таких молекул в газе 10-4%.  В порах настоящего катализатора и реагирующих газов мы имеем кнудсеновское течение вплоть до давления 5 МПа.

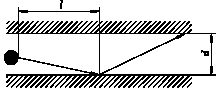
    d  - диаметр поры,   l  - длина свободного пробега молекулы (l >>d).

Рис. 1 расположение молекулы газа в нано поре.

На рис. 1 видно как отдельная молекула перемещается внутри нано поры, молекула в основном сталкивается со стенкой. От осцилляторов молекул составляющих твёрдую стенку молекула получает энергию, причем в основном вращательную, т.к. центр массы смещен по отношению к форме контактной пленки молекулы. Твердый состав катализатора основан на Al2O3. При формировании гранул катализатора добавляются связующие вещества и окислы никеля до 18% масс. При обработке пасты составляющей гранулу катализатора горячими восстановительными газами гранулы образуют пористую структуру с нано порами. Окислы никеля восстанавливаются до никеля и превращаются в никелевые нано дендриты [4]. Нано дендриты имеют не регламентированную вытянутую форму с изменяющемся диаметром. Молекулы СН4 адсорбируются в углубления нано дендритов (наименьший диаметр дендрита) теряют водород и образуют углеродное кольцо, которое разрывает дендрит.   

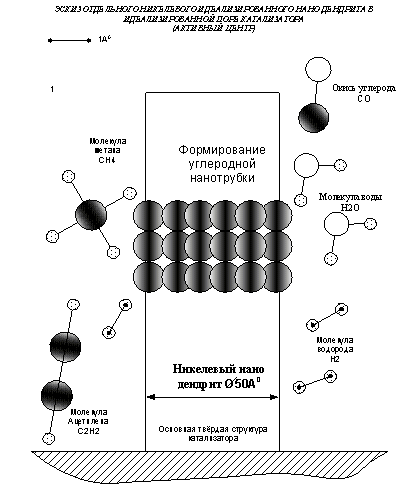
Рис.2 Гипотетический идеализированный никелевый нано дендрит.

Далее образуются новые кольца углерода, образуя многослойные углеродные

нано трубки. Эти трубки создают поверхность для 2-рой реакции (1). Реакция С +  Н2О = СО + Н2  (3) требует для взаимодействия воды с углеродом энергию 1,22 эВ. На рис. 3 показан эскиз плёночной модели в молекулы воды с названной энергией. В процессе движения такой молекулы в нано поре помимо поступательной энергии молекула приобретает энергию вращения которая в 5 раз больше энергии поступательного движения молекулы. В таком состоянии вода реагирует с углеродом нано трубок по реакции (3)[2.7].

 

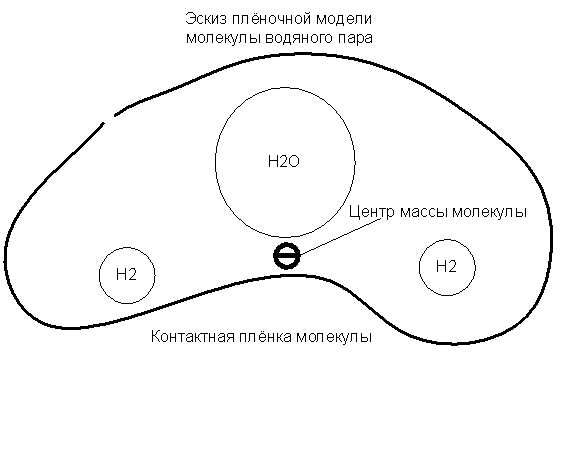
Рис.3 Эскиз молекулы воды с общей энергией 1,22 эВ.

Заключение.

         На основании экспериментов [7] можно сказать, что в реакции (1) реагирующие молекулы приобретают энергию вращения в несколько раз большую, чем энергия поступательного движения. Поэтому используя известные законы молекулярной и статистической физики можно предложить уравнение заменяющее уравнение Аррениуса. Все ранее известные кинетические зависимости для реакции (1) справедливы только для реакторов, на которых осуществлялась реакция (1) и проводились необходимые измерения.

Литература:

1. Igumnov V.S. “Technical and technological methods of realization of steam catalytic conversion of natural gas with a methane-water proportion close to stoichiomythic ratio” , Hydrogen materials science and chemistry of carbon nanomaterial, NATO security science setias – A: Chemistry and Biology,  The NATO Programmer for Security through science.  Page 555-561.  2007.

2. Игумнов В.С., Лозина Е.Ю. Статистический вес образования углеродных наноструктур  в условиях каталитического взаимодействия  метана с водяным паром, Доклад, MATERIALY  VII  MZINARODNI VEDECKO – PRAKTICKA KONFERENCE; ‘ VEDA A TECHNOLOGIE: KROK DO BUDOUCNUSTI – 2012”  Dil 31 (том 31). 27 unojra – 05 brezen 2012 roku, Praha, Publishing House “Education ana Science” s.r.o. 2012, ISBN 978-966-8736-05-6.

3. Слинько М.Г., Дильман В.В., Маркеев Б.М., Кронберг А.Е. Моделирование реакторов с неподвижным слоем катализатора. Химическая промышленность, №11, М.,1980.

4. Игумнов В.С.,   «Углеродные наноструктуры – промежуточная стадия в каталитической конверсии метана» // III Международный симпозиум «Фуллерены и фуллереноподобные структуры в конденсированных средах», июнь, 2004, Минск.

5. Igumnov V.S. “Catalytic conversion of hydrocarbons in the ratio of steam/gas close to stoichiometric”. Catalysis in Industry, Vol. 3, N1, March 2011, p 81-86,    

6. “PERSPEKTYWICZNE OPRACOWAVIA SA NAUKA I TECHNIКAMI – 2011”, 07-15 Listopada 2011 roku, Vol.48 Chemia i chemiczne technologie, Przemysl, Nauka i studia, 2011, сборник докладов,

p. 54-59.      Игумнов В.С., Вавилов С.Н., Тепляков И.О., Гусева А.А., Кубриков К.Г., Мамайкин Д.С., Виноградов Д.А. «Теплообмен при каталитической паровой конверсии природного газа в трубе».

7. Игумнов В.С., Вавилов С.Н., Тепляков И.О., Гусева А.А., Лозина Е.Ю., Кубриков К.Г., Мамайкин Д.С., Виноградов Д.А. Испытания  эффективности загрузки и формы катализатора и ингибирующей насадки конверсии природного газа в обогреваемой трубе. Интегральные эксперименты. Сборник докладов на международной конференции, VIII MEZINARODNI VEDECKO-PRAKTICKA KONFERENCE “APLIKOVANE VEDECKE NOVINKY-2012” ; PRAHA 27.07. – 05.08.2012. ISBN 978-966-8736-05-6.