6 страниц

Сагателян А.К.

(Государственный Инженерный Университет Армении)

Принципы построения модулярных сумматоров

В данной работе показаны методы  построения, эффективных с точки зрения быстродействия, модулярных сумматоров с применением современных методов проектирования и логического синтеза. Предлагаются варианты построения сумматоров данного типа как с использованием, так и без использования запоминающих устройств.

Ключевые слова: модулярная арифметика, модулярные сумматоры, система остаточных классов, LUT – таблица (Look-Up-Table), структура устройства модулярного сумматора.

В цифровых системах модулярная арифметика используется как средство повышения быстродействия, в цифровой обработке сигналов, криптографии и т.д.

Так как возрастает актуальность аппаратной реализации криптографических устройств, то появляется необходимость аппаратной реализации отдельных блоков выполнения арифметических операций в системе остаточных классов(СОК). [1]

В СОК каждое число А, которое является многоразрядным в позиционной системе счисления представляется в виде малоразрядных чисел, которые являются остатками от деления числа А на взоимопростые основания. Остатки форморуются в табличной  арифметике, при которой результат операции не вычисляется каждый раз, а рассчитывается один раз, помещается в запоминающем устройствт (ЗУ) и при необходимости считывается из него. То есть операция в системе остаточных классов выполняется за один период синхронизирующей частоты (машинный такт).

Так как в СОК используются модулярные операции для большей эффективности необходимо использовать специально спроектированные для СОК сумматоры и умножители.

В данной статье рассмотрены принципы построения модулярных сумматоров с использованием и без использования ЗУ. Существует достаточно большое количество подходов к реализации сумматоров по модулю m [2].

Схема модулярного суммирования, представленная на рисунке1,  вычисляет сумму по модулю m , т.е. (a+b)mod m, с помощью большой LUT – таблицы (Look-Up-Table) размером 22n x M, где M=log2m, а n разрядность  чисел  a и b .  

Два n разрядных числа a  и b подаются на адресные входы  LUT -таблицы, из которой просто выби-рается ответ.

Это решение очень удобно для двух чисел не очень большой разряд­ности.
 

Рис.1 Схема модулярного суммирования, с помощью большой LUT – таблицы
 
 

 

 

 

 

 

 

 


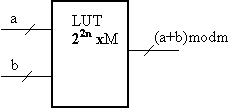
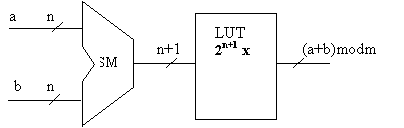
 Для чисел большей разрядности память LUT-таблицы  была бы значительного размера и для этих случаев предлагается следующая схема модулярного суммиро-вания, представленная на рисунке 2.

 

 

 

Рис.2  Схема модулярного суммирования, с предварительным суммированием и LUT – таблицы
 
 

 

 


Это предложение основано на предварительном обычном суммировании чисел a  и b и одной  LUT-таблицы размером  2n+1x M, содержащей все возможные значения для  (a+b)modm. Сокращение размера таблицы с 22nxM до 2n+1xM дает    возможность расширять набор модулей.

Третий вариант схемы модульного суммирования без использования LUT–таблиц, наиболее распространенный, предполагает наличае управляющего автомата и основан на использовании двух сумматоров для вычисления результата в соответствии с выражением (1):

 

 


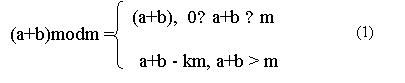
где k = 1, 2, 3,… .

Блок-схема алгоритма  для такого варианта модулярного суммирования представлена на рисунке 3.

n разрядные двоичные числа  a и b устанавливаются в соответствующие регистры  ra и rb. Дополнительный код значения модуля m устанавли-вается в регистр rmod. Сумматор SM1  выполняет обычное двоичное сумми¬рование, результат которого устанав¬ливается в rsm и дублируется в   rmem. Сумматор SM2 вычисляет разность a+b-m и анализируя знак результата выбирает или повторение цикла, или присвоение значения (a+b)modm последнего содержимого rmem. Коэффицент k в выражении указывает на количество циклов выпо묬нения условия X1-проверки зна¬ка содержимого регистра rsm. После вычисления значения (a+b)modm, управляющий автомат передает операционному устройству сигнал ready – сигнал окончания выполнения операции модулярного суммирования чисел.

 

 

 

 

 

 

 

 

 

 


                                                                                                

 

 

 

 

 

 

 

 

 

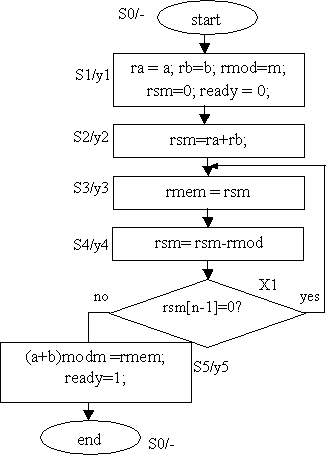
Рис.3 Блок-схема алгоритма модулярного суммирования без использования LUT – таблицы
 
 

 

 


Произведена разбивка управляющего автомата модели Мура, граф перехода которого представлен на рисунке 4.

 

 

 

 

 

 

 


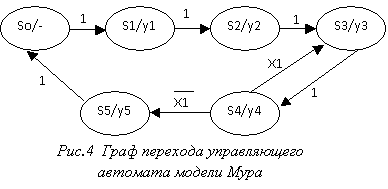
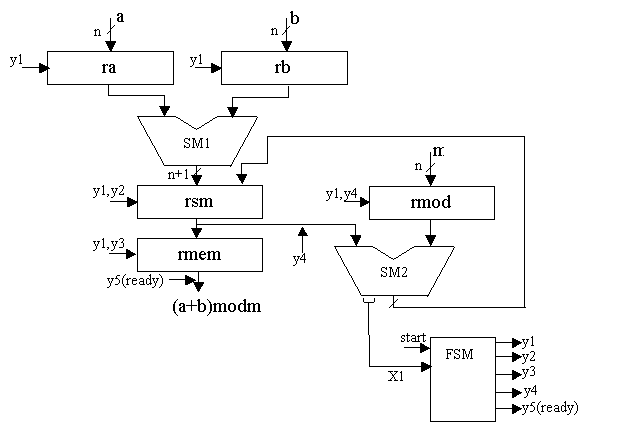Структурная схема устройства модулярного суммирования, с управляющими сигналами, представлена на рисунке 5. Управляющие сигналы отмечены в соответствии с операционными блоками блок-схемы алгоритма (рисунок 3), и вырабатываются управляющим автоматом FSM( Final State Machine).[3-4]

 

 

 

 

 

 

 

 

 

 

 

Рис.5 Структурная схема устройства модулярного суммирования
 
 

 


Выводы: из приведенного выше можно сделать вывод, что предложенные способы проектирования модулярных сумматоров являются более эффективными с точки зрения быстродействия, по сравнению с традиционным способом суммы по модулю m, т.е. обычное суммирование и последующее деление на значение модуля m, т.к. процесс нормализации делителя (в данном случае значение модуля m ), вычисление каждого разряда частного и, наконец, возможная неодходимость в нормализации конечного остатка, который и есть результат (a+b)modm,   является причиной уменьшения быстродействия. Кроме того для RTL–описания на языке Verilog каждый блок отдельно описывается с помощью процедурного оператора always, а если он является комбинационной схемой, то может описыватся также с применением оператора assign. В результате получится RTL–описание устройства, на основе которого можно синтезировать схему.

Литература

1.Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах.-М.:Советское радио, 1968.

2.Исаева Т.Ю., Корнилов А.И. Алгоритм декомпозиции логических функций, ориентированный на синтез быстродействующих цифровых устройсв// Информационные технологии.-N4, 2001.-с26-31.

3. Aoki, Ecei,Tohoku. Hardware algorithms for arithmetic modules.

4.Wakerly J.F. Digital Design. Principles and Practices. 4th Edition.- New Jersey, 2006.