Vlasenko I.B.¹, Shevtsov S.N.², Huang Jyun-Ping³

¹Don State Technical University, ²South Center of Russian Academy,
Rostov on Don, Russia

³National Kaohsiung Marine University, Kaohsiung, Taiwan R.O.C.

On the Contact Stiffness of Anti-Friction Polymeric Composite Covering Operated in the Fluid Media

The polymeric composite antifriction coverings are widely used in the modern bearing assemblies, which operated in the chemically active aqueous solutions. These coverings have the good wearing resistance at the high contact stresses and slipping velocities [1]. Such coverings produced from the fabrics with different weavings impregnated by the polymeric resin that ensure the required contact stiffness. At the same time the fabric structure creates the regular micro-relief on the friction surface, and the micro cavities on this surface contain small volumes of fluid which gives to these coverings the ability of self-lubrication. The most important features of antifriction coverings are the wear intensity, the creep under the normal contact stress, activated by the thermal effect due to friction, and also the elastic contact stiffness needed to maintain the pre-assigned gap at the action of the high radial loading. Some works, e.g. [2] communicate about experimentally established increasing on 20…30% of the contact stiffness of polymeric composite coverings at operation in the fluid media. This paper presents an approach to the modeling of this phenomenon and some results obtained by the finite element implementation of contact problem for the stiff shaft and polymeric composite covering with the presence of fluid.

It has been established [1, 2] that weight of the polymeric composite covering is gained on 5…7% due to water absorption. We assumed the increasing of the contact stiffness of moistened polymeric composite is caused by the presence of small amounts of fluid in the closed pores of the composite structure. In order to build our model some assumptions have been adopted.

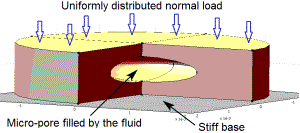
Assuming regular structure of composite based on the fabric the micro-domains of fluid have been adopted as the ellipsoid of revolution with the similar dimensions and lesser axis is normal to the friction surface (see Fig.1, a). All pores filled by the fluid are closed and not connected one with other. Tangent stresses due to friction are negligible, so, they are not taken into account. All stress and strains are adopted as quasi-static. Material of covering is adopted as elastic transversally isotropic with the elastic properties early determined according to [3]. The fluid is compressible with a compressibility corresponding to the water. These assumptions allowed to consider the studied system as axially symmetric circular disk which is clipped from the anti-friction covering with the small elliptic fluid inclusion (see Fig. 1, a).

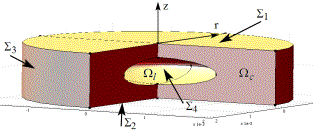
Figure 1. Schematic view of the studied model: Geometry of subdomains (left) and designations of boundaries (right)

The constructed model take into account the change of the fluid volume at the external loading, and due to change of the fluid volume the hydrostatic pressure is applied to the interface boundary between fluid and elastic material. A correct description of these phenomena is ensured by the joint consideration of global coordinate frame together with local frame which moves according to deformations of elastic body. To do this the equations of the moving finite element mesh have been introduced, and these equations allow to calculate the fluid volume on each iteration step. The appropriate numerical technique named as the Arbitrary Lagrangian-Eulerian – ALE method [4] imply a determination of the finite element mesh coordinates from the solution of mechanical sub-problem

,

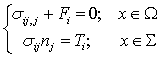where is the stress tensor; are the densities of volumetric forces and surface traction respectively, is normal to the surfaces, is coordinate of arbitrary point in the elastic body.

So, the solved joint problem includes equations of elasticity, hydrostatic equation of the compressible fluid in the varied volume, which is determined by the moving mesh equations. The problem has been implemented in the commercial finite element soft package Comsol Multiphysics 3.5. The problem is stated as static with linearly increasing normal force on the surface .

The finite element model has been simulated at the different volumetric content of fluid. The changed geometry of elastic and fluid subdomains, contour lines of von Mises stress, and strain (arrows) in the covering are presented on the plot (see Fig. 2).

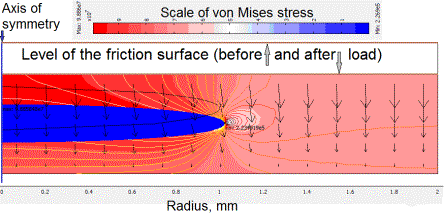
Figure 2. The fields of displacements and von Mises stress in the layer of anti-friction polymeric composite covering which contains 5.6% (volumetric) of absorbed water

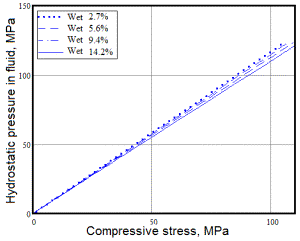
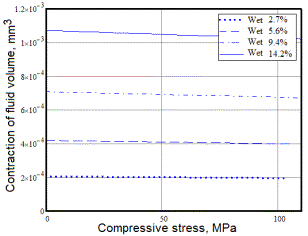
Calculation results show the considerable increase of internal pressure in the pore filled by water and some decrease of the fluid volume that caused by deformation of initially ellipsoidal shape of pore (see Fig. 3).

Figure 3. The dependencies of hydrostatic pressure in the liquid inclusion and reduction of its volume on the applied compressive stress at the different volumetric content of water

Such pressure can lead to the delamination and destruction of the covering structure, all the more so, von Mises stress is concentrated near pore surface with high curvature (see Fig. 2). The dependence of the effective compressive elastic modulus on the water content can be good described by the polynomial model presented on the Fig.3. As on can see graph of this dependence is growing with diminished rate. Thus, experimentally established increasing of the contact stiffness of anti-friction polymeric composite coverings in the fluid media can be satisfactorily explained by the proposed model, which further identify a riskiness of extreme contact forces for the integrity of anti-friction covering.

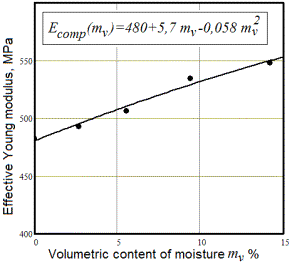
Figure 4. The dependence of effective compressive module of covering on the volumetric content of water: points – finite element calculation results; solid line – empiric polynomial model of dependence shown on the inset

References

1. Gardos M.N. Self-lubricating composites for extreme environmental conditions // In Friction and Wear of Polymer Composites, Ed. K.Friedrich, Elsevier Science Publ., Amsterdam, 1986, p.397-448

2. Власенко И.Б. Вязкоупругие свойства антифрикционных покрытий в водных средах // Трение и смазка в машинах и механизмах, 2012, №12, с. 34-38

3. Shevtsov S. et al. Polymeric Composite Shear Elastic Constants Determination on the Basis of Modified Technique // Proc. of the 2^nd Int. Conf. “From Scientific Computing to Computational Engineering” 2nd IC-SCCE, Athens, Greece, 5-8 July, 2006, 8 p.

4. Donea J., Huerta A., Ponthot J.-Ph. and Rodrıguez-Ferran A. Arbitrary Lagrangian–Eulerian Methods // In Encyclopedia of Computational Mechanics, Ed. Erwin Stein, Rene de Borst and Thomas J.R. Hughes. Vol. 1: Fundamentals. 2004, John Wiley & Sons, Ltd., p.125-149