Математика/ 5. Математическое моделирование

Д.т.н. Лукашевич А.А.

Санкт-Петербургский государственный политехнический университет,

Россия

Численные модели контактного взаимодействия упругих тел с применением контактных конечных элементов

Конструктивно нелинейные задачи с односторонними связями и трением при неизвестной заранее зоне контакта часто встречаются при расчете различного рода конструкций и сооружений. Например, технологические и деформационные швы, имеющие место в массивных сооружениях, могут раскрываться и закрываться, как с проскальзыванием, так и со сцеплением контактирующих поверхностей, при различных сочетаниях внешних нагрузок. То же самое может происходить на контакте подошвы сооружения с основанием, либо на отдельных опорах, допускающих отрыв либо проскальзывание опирающейся на них конструкции. В то же время именно состояние контактной зоны нередко является определяющим при оценке напряженно-деформированного состояния, прочности и работоспособности конструкций и сооружений.

Особый интерес представляют задачи с усложненными условиями контакта, учет которых приближает расчетную схему к реальным условиям работы сооружения. Это, например, контактное трение при зависящих от решения нормальных силах взаимодействия, учет деформаций и начальной прочности односторонних связей, учет последовательности возведения и загружения сооружения, динамического действия нагрузки и т. п. В этих случаях контактная задача усложняется в математическом отношении и усложняется ее численное решение. Поскольку учет перечисленных выше условий делает решение подобных задач зависящим от характера и истории загружения, представляется целесообразным моделировать контактное взаимодействие и, соответственно, строить решение на основе метода пошагового анализа.

В настоящей работе при решении односторонних контактных задач используются непосредственно конечно-элементные модели и алгоритмы их численной реализации. Так, для моделирования односторонних связей применяются специальные контактные конечные элементы (ККЭ), которые вводятся на участках возможного контакта взаимодействующих тел, тем самым дискретизируя некоторый тонкий слой (фиктивный или имеющий место в действительности) между контактирующими поверхностями. Этот контактный слой объединяет взаимодействующие тела в единую систему и, благодаря приданным ему особым свойствам, учитываемым посредством численного анализа, может удовлетворять необходимым условиям контакта. Такой подход позволяет конструктивную нелинейность заданной системы, то есть задачу с односторонними связями и трением между взаимодействующими телами, свести к рассмотрению самого нелинейного дискретного контактного слоя. В нашем случае предлагается использовать контактные конечные элементы в виде стержневой системы – плоской или пространственной рамы [1]. Данные ККЭ взаимодействуют с обычными конечными элементами двумерных либо трехмерных задач и обеспечивают контакт между узлами сетки, расположенными на граничных поверхностях контактирующих тел (рис. 1).

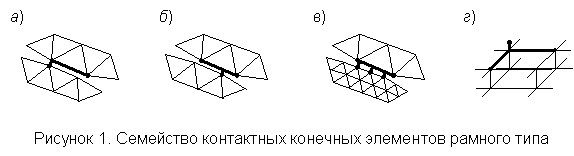
При использовании указанных контактных элементов нет необходимости в совпадении координат узлов контактирующих поверхностей, т. е. могут применяться несогласованные сетки. ККЭ могут вводиться как сразу, так и последовательно, по мере установления контактов между граничными поверхностями тел, выполняя тем самым функции регистрации состояния участков контакта (или отрыва) соприкасающихся поверхностей, а также моделируя различные условия контакта (отрыва, сцепления, проскальзывания и т. д.). Кроме того, посредством ККЭ могут учитываться различные свойства односторонних связей, такие, например, как упругая податливость, физическая нелинейность, начальная прочность и др. Моделирование условий контакта осуществляется посредством изменения физических свойств контактного слоя, которые выражаются через жесткостные характеристики отдельных стержней рамных ККЭ.

Рассмотрим, в частности, плоскую контактную задачу для линейно упругих тел и , между граничными поверхностями которых (, ) имеют место односторонние связи с кулоновским трением. Для моделирования состояния контакта в дискретной расчетной модели МКЭ используем предложенные плоские рамно-стержневые контактные элементы (рис. 2).

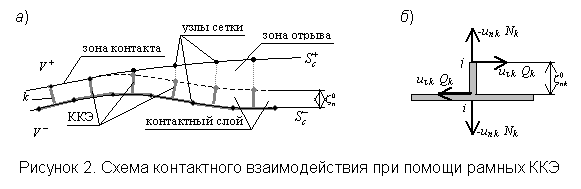
Граничные условия на контакте при этом выражаются через усилия и деформации в каждом отдельном ККЭ:

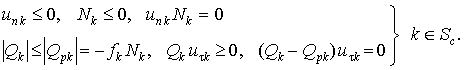(1)

Здесь – продольная и поперечная силы в k-м ККЭ;  – взаимное смещение противолежащих узлов на и () соответственно по нормали и по касательной; f – коэффициент трения.

Для решения контактных задач с односторонними связями могут применяться как методы нелинейного программирования, сводящиеся, в конечном счете, к итерационным процедурам, так и инкрементальные (пошаговые) методы. В последнем случае численная реализация граничных условий (1) будет осуществляться посредством пошагового анализа процесса нагружения и изменения состояния контакта в данной рамно-стержневой модели. Момент перехода от одного состояния к другому представляет собой соответственно событие выключения, включения односторонней связи, проскальзывания или зацепления. Метод пошагового анализа является наиболее эффективным для рассматриваемого класса контактных задач, кроме того, имеется возможность управления поведением дискретного контактного слоя в соответствии с характером нагружения, текущим состоянием контактной зоны, уровнем напряженно-деформированного состояния и т. д.

Статическое нагружение моделируется посредством пошагового приложения заданной нагрузки. Будем предполагать, что между двумя последовательными событиями система деформируется по линейному закону – в этом случае в пределах каждого шага строится решение линейно упругой задачи, а события на контакте определяются согласно схеме простого нагружения. В результате решение конструктивно нелинейной контактной задачи будет представляться в виде решения последовательности некоторого числа линейных задач, при последовательном же изменении рабочих схем сооружения. Порядок расчета здесь состоит из пробных и основных шагов нагружения. Из анализа пробного шага определяется момент наступления очередного события. В результате основного шага устанавливается новое состояние контакта и, в свою очередь, из анализа изменения рабочей схемы назначается следующий пробный шаг. Это позволяет уточнять величину не только текущего шага нагружения, но и прогнозировать дальнейшие шаги и, таким образом, строить оптимальный, с точки зрения продолжительности и трудоемкости, процесс нагружения [2].

Момент наступления события проскальзывания (т. е. величина основного (s+1)-го шага) для k-й связи, находящейся до этого в состоянии контакта со сцеплением (, ), определяется следующим выражением:

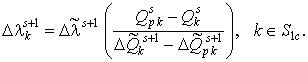(2)

Переход из состояния скольжения в состояние сцепления на (s+1)-м шаге определяется условием: , , .

Моменты выключения (отрыва) или включения (контакта) для k-й связи, находящейся до этого в состоянии контакта (, ) или в состоянии отрыва (, ):

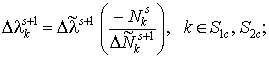
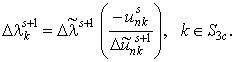(3)

Здесь величины – приращения контактных усилий и взаимных перемещений для k-го ККЭ на пробном шаге .

Возможные случаи изменения предельной силы трения на (s+1)-м шаге, а также соответствующие схемы уточнения текущего основного шага и корректировки контактных усилий (для k-го ККЭ) приводятся ниже.

1. Приращение предельной поперечной силы превышает приращение поперечной силы в k-м ККЭ, что соответствует условию допредельного трения – устанавливается состояние сцепления и выполняется перерасчет шага.

2. Приращение предельной поперечной силы меньше, чем приращение поперечной силы – состояние скольжения на k-м контакте сохраняется и производится корректировка значений поперечных сил в ККЭ:

, (4)

где – невязка поперечных сил; – приращение предельной поперечной силы на шаге (при заданной точности вычислений ):

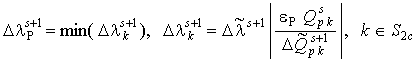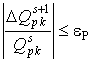, где . (5)

К соответствующим контактным узлам на граничных поверхностях взаимодействующих тел прикладываются компенсирующие силы:

. (6)

3. Если предельная поперечная сила на шаге уменьшается: , то уточнение шага и корректировка контактных усилий производится согласно (4)–(6).

При динамическом действии нагрузки конструктивная нелинейность проявляется в смене рабочих схем сооружения во времени. Момент времени изменения состояния контакта (т. е. наступление очередного события) в этом случае определяется путем пошагового (по времени) анализа рамно-стержневой контактной модели при использовании соответствующих аппроксимирующих выражений для перемещений, скоростей и ускорений на шаге Δt. При этом корректируется продолжительность временного шага и производится его перерасчет. В результате устанавливается новое состояние контакта на данный момент времени и, таким образом, меняется текущая рабочая схема сооружения.

Запишем конечно-элементную формулировку для динамической контактной задачи. Матричное уравнение движения здесь представляется в виде, позволяющем решение конструктивно нелинейной динамической задачи свести к решению последовательности линейных динамических задач на основе пошагового по времени анализа состояния контакта для рассматриваемой дискретной модели МКЭ:

(7)

Для численного интегрирования уравнений (7) используется конечно-разностная схема Ньюмарка. В любой момент времени в пределах текущего шага Δt значения перемещений, скоростей и ускорений рассчитываются по формулам:

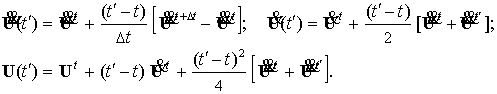(8)

При наличии односторонних связей и кулоновского трения, кроме того, должны выполняться граничные условия на контакте, записанные для момента времени t:

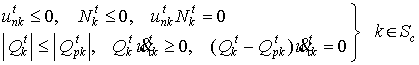. (9)

Здесь – скорость взаимного касательного перемещения противолежащих узлов k-го ККЭ в момент времени t. Состояния на контакте будут определяться следующими условиями: при сцеплении , , , ; при проскальзывании , , , ; при отрыве , .

Численное решение динамической контактной задачи, таким образом, будет заключаться в проведении процесса пошагового интегрирования по времени уравнений (7) при выполнении условий на контакте в виде (9). Соответствующие выражения для определения момента времени наступления ближайшего события – проскальзывания, зацепления, отрыва или контакта для k-й связи здесь имеют следующий вид [3]:

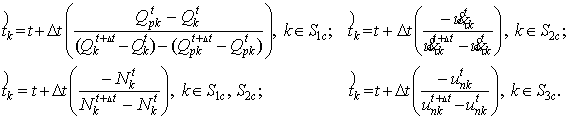(10)

С помощью аппроксимирующих выражений (8) дополнительно может быть произведено итерационное уточнение момента времени , затраты времени счета при этом возрастают незначительно.

Приведенные модели ККЭ и методы их расчета нетрудно распространить на решение задач с односторонними связями при учете физических свойств контактного слоя, а также других дополнительных факторов. Так, при учете упругой податливости в односторонних связях [4] граничные условия (1) примут следующий вид:

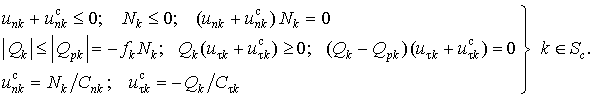(11)

Здесь – продольная и поперечная деформация k-го ККЭ (соответствующие обжатию и сдвигу упруго-податливого контактного слоя с начальной толщиной); , , , – характеристики жесткости и податливости ККЭ соответственно в нормальном и касательном направлениях; – площадь контакта, относящаяся к ККЭ. Физическая нелинейность контактного слоя здесь также может быть сведена к внутренней нелинейности самих рамных контактных элементов – при этом нелинейные свойства слоя будут задаваться через нелинейные характеристики отдельных стержней ККЭ.

При учете начальной прочности контактного шва на разрыв и срез условия на контакте запишутся в следующем виде:

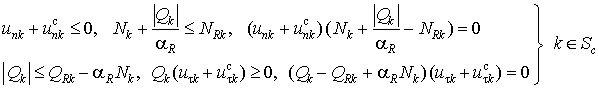. (12)

Здесь , – предельные контактные усилия растяжения и сдвига для k-й дискретной односторонней связи (т. е. k-го ККЭ).

Подчеркнем, что условия (12) справедливы только до момента разрушения связей в данной точке контакта, после чего будут действительны условия (11), описывающие односторонние связи с трением. Внеся соответствующие дополнения в алгоритм, обеспечиваем в одном пошаговом процессе одновременный учет прочности контактного шва, а также раскрытия или трения его поверхностей на участках, где сцепление разрушено.

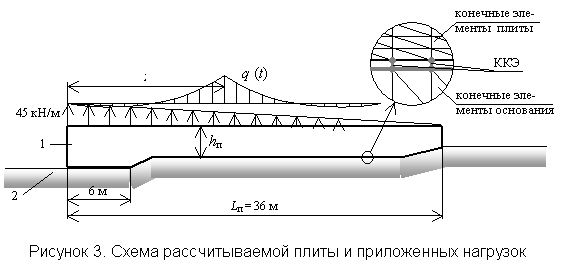Приведенные расчетные модели и методы реализованы в комплексе вычислительных программ, предназначенных для решения статических и динамических задач контактного взаимодействия. С их помощью выполнены расчеты ряда конструкций и сооружений с односторонними связями при учете соответствующих условий контакта и характера внешних воздействий. На основе анализа полученных результатов сделаны предложения, касающиеся конструктивных решений сооружений и действующих на них нагрузок [5,6].

Литература

1. Лукашевич А. А. Построение и реализация схем прямого метода конечных элементов для решения контактных задач // Изв. вузов. Строительство. 2007. № 12. С. 18–23.

2. Лукашевич А. А. Решение контактных упругих задач с трением Кулона при пошаговом нагружении // Изв. вузов. Строительство. 2008. № 10. С. 14–21.

3. Розин Л. А., Лукашевич А. А. Численное решение контактных задач с трением при динамических воздействиях // Научно-технические ведомости СПбГПУ. 2010. № 4 (110). С. 288–294.

4. Лукашевич А. А. Решение контактных задач при учете податливости и прочности односторонних связей методом пошагового нагружения / А. А. Лукашевич // Вестник гражданских инженеров. 2009. № 3 (20). С. 18–23.

5. Бухарцев В. Н., Лукашевич А. А. Решение задачи о взаимодействии водобойной плиты крепления с основанием при пульсации давления в сбрасываемом потоке // Гидротехническое строительство. 2010. № 4. С. 52–55.

6. Бухарцев В. Н., Лукашевич А. А. Расчет сооружений с учетом последовательного возведения и наличия односторонних связей на контактах // Научно-технические ведомости СПбГПУ. СПб. 2009. № 4-1 (89). С. 74–78.