И. А. Кострикина, Е. Н. Галкина

Способ оценки метрологической надежности средств измерений по результатам ускоренных испытаний

Расширение сфер применения средств измерений (СИ), многообразие и сложность измерительных задач, рост ответственности функций, возлагаемых на СИ, приводят к необходимости улучшения эксплуатационных, в первую очередь надежностных характеристик этих изделий. Проблема повышения надежности связана в основном с усложнением конструкции приборов, повышением требований к нормируемым метрологическим характеристикам, условиям эксплуатации, с наличием в составе СИ средств вычислительной техники и т.д.

Для СИ важнейшими показателями метрологической надежности являются метрологические характеритсики, которые обуславливают возможность измерения физических величин с погрешностью, не превышающей допускаемых пределов. В процессе эксплуатации одна или несколько метрологических характеристик конкретного экземпляра СИ, изменяясь, могут выйти за пределы, нормируемые в технической документации для данного типа СИ, и тем самым перевести СИ в неработоспособное состояние.

Одной из основных форм поддержания СИ в метрологически исправном состоянии является его периодическая поверка. Она проводится метрологическими службами согласно правилам и методикам, изложенным в специальной нормативно-технической документации. Поверку необходимо проводить через определенные интервалы времени [1]. При этом возникает проблема, которая заключается в следующем. С одной стороны для снижения риска эксплуатации метрологически неисправного оборудования и предотвращения аварийных ситуаций поверка должна проводиться как можно чаще. С другой стороны, частые поверки оказываются экономически нецелесообразными и трудозатратными как человеческих, так и аппаратных ресурсов. То есть возникает задача определения оптимального интервала между поверками СИ.

Установление значения оптимального интервала между поверками СИ в соответствии с рекомендациями [2] не решает проблему: доступных данных, как правило, недостаточно. Кроме того, если с корректировкой межповерочного интервала СИ в процессе эксплуатации вопрос может быть решен на основе анализа данных полученных периодическими поверками или калибровками, то для назначения первичного межповерочного интервала СИ вопрос остается открытым, хотя метрологическая надёжность закладывается при проектировании и разработке СИ.

Согласно [2], при назначении первичного интервала между поверками СИ могут быть приняты во внимание:

- результаты испытаний СИ или его отдельных блоков, данные о нестабильности элементов СИ;

- показатели надежности СИ;

- данные об опыте эксплуатации СИ-аналогов.

Определение интервала между поверками СИ по итогам длительных испытаний, во-первых, является дорогостоящей процедурой, а, во-вторых, результат таких испытаний теряет свою ценность при последующих изменениях в технологии производства, например, при замене поставщика компонентов или материалов.

Назначение интервала между поверками СИ по аналогу вносит неопределенность в связи с возможным отличием в свойствах материалов и компонентов, а также в особенностях принятой технологии и условиях эксплуатации. Возрастающая скорость изменения технологий и материалов усугубляет это обстоятельство.

При изучении вопроса авторами были проанализированы достоинства и недостатки методов назначения МПИ на основе [2-5].

В таблице 1 приведены основные достоинства и недостатки различных методов назначения интервалов между поверками СИ.

Таблица 1 - Методы назначения интервалов между поверками СИ.

Методы назначения интервалов между поверками	Достоинства	Недостатки
1 На основе статистически скрытых и явных отказов	Высокая достоверность результатов испытаний	Большое количество экспериментальных данных по процессам изменения во времени; исследования весьма трудоемки
2 По экономическому критерию	Минимизация расходов на эксплуатацию СИ; устранение последствия от возможных ошибок, вызванных погрешностями измерения	Применение приближенных моделей
3 Произвольное назначение первоначального интервала между поверками СИ с последующей корректировкой в течение всего срока службы СИ	Минимальные финансовые и временные затраты	Определение первого интервала между поверками СИ; не на все СИ существуют нормативные документы с рекомендациями первого интервала между поверками СИ; отсутствуют данные о надежности элементов
4 Назначение интервалов между поверками СИ по аналогам	Отсутствие финансовых и временных затрат	Результат аналогов не всегда корректно применять к новому разрабатываемому средству измерения; у приборов аналогов отсутствуют данные о параметрах надежности
5 Расчет интервалов между поверками СИ по показателям надежности (интенсивности отказов λt, или наработки на метрологический отказ Тмо.)	Высокая достоверность результатов испытаний	Большое количество экспериментальных данных по процессам изменения во времени; исследования весьма трудоемки
6 Расчет интервалов между поверками СИ по анализу прогрессирующей составляющей погрешности СИ	Отсутствие финансовых затрат и высокая достоверность результатов испытаний	Необходимость наличия сведений о поверке за длительный промежуток времени, а также затраты на постоянный контроль необходимости проведения поверки

Как видно из таблицы 1, ни один из приведенных методов не дает полной достоверной оценки интервалов между поверками СИ.

Наиболее достоверный результат назначения интервалов между поверками СИ может быть получен при проведении натурных испытаний в течение сроков наработки до отказа. Однако натурные испытания эффективно проводить при небольших наработках на отказ. Проведение натурных испытаний является очень трудоемким и приводит к затратам финансовых и человеческих ресурсов. В связи с этим целесообразно проводить форсированные испытания, но с возможностью сохранения картины потоков отказов дефектов СИ.

На основании вышеизложенного и [6] авторами предложена методика назначения интервала между поверками по результатам ускоренных испытаний.

В данной методике в качестве критерия нормируемого показателя предлагается использовать предел допускаемых значений вероятности метрологической исправности компонента в момент очередной поверки (либо предел средней доли компонентов забракованных при поверке, (). Рекомендуемые значения 0,90…0,95 [2, 7].

Применительно к выбранному критерию определения интервала между поверками () алгоритм испытаний заключается в следующем (рисунок 1).

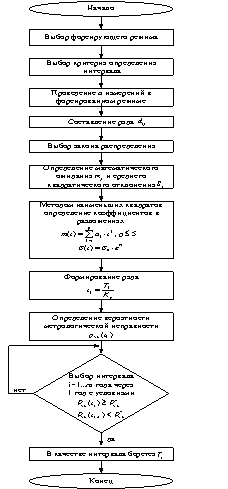
Рисунок 1 – Алгоритм определения интервала между поверками по результатам ускоренных испытаний

Проводится n измерений характеристик компонентов каждого типа прибора. Составляем ряд , где i - номер образца компонента данного типа, j - номер измерения.

Закон распределения выбирается в процессе анализа опытных данных о наработках аналогичных изделий до отказа. При выборе теоретического закона распределения необходимо учитывать информацию об изменениях, происходящих в объектах перед наступлением отказов, т. е. о характере физических процессов, протекающих в объекте.

Весьма удобной представляется методика определения закона распределения по коэффициентам асимметрии и эксцесса путем проверки гипотез. Задача проверки гипотезы о законах распределения по коэффициентам асимметрии и эксцесса начинается с выбора нулевой гипотезы. По данным эксперимента определяются статистические оценки коэффициента асимметрии и коэффициента эксцесса . Например, для нормального закона распределения коэффициенты выглядят следующим образом:

;

где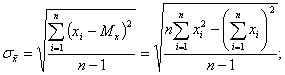

Значение оценок и позволяют приближенно определить закон распределения. Для этого по полученным значениям оценок на диаграмму наносится точка (;).

Задача проверки гипотезы о виде распределения происходит по критерию согласия Пирсона . Это один из основных критериев, который можно представить как сумму отношений квадратов расхождений между теоретическими и эмпирическими частотами к теоретическим частотам

где - число групп, на которые разбито эмпирическое распределение;

- наблюдаемая частота признака в i-й группе;

- теоретическая частота.

Для распределения составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости и степеней свободы . Уровень значимости - вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. Р – статистическая достоверность принятия верной гипотезы. В статистике чаще всего пользуются тремя уровнями значимости:

, тогда;

, тогда ;

, тогда может быть отвергнута правильная гипотеза.

Число степеней свободы определяется как число групп в ряду распределения минус число связей: . Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты. Например, при выравнивании по кривой нормального распределения имеется три связи. Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как Для оценки существенности, расчетное значение сравнивается с табличным .

При полном совпадение теоретического и эмпирического распределения , в противном случае Если , то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем. В случае, если то гипотезу принимаем и с вероятностью можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно. Критерий согласия Пирсона используется, если объем совокупности достаточно велик (N>50), при этом, частота каждой группы должна быть не менее 5.

Для каждого номера измерения j определяются математическое ожидание и среднее квадратическое отклонение

например, для нормального закона распределения

По полученным значениям методом наименьших квадратов находятся коэффициенты в разложениях

.

Формируется ряд

,

где - значения интервала между поверками из ряда 1,2,3 и т. д., через 1 год;

- коэффициент ускорения для данного компонента.

Вероятность метрологической исправности в момент времени определяется по формуле

например, для нормального закона распределения

,

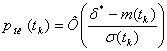
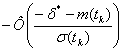где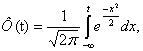

- предел допускаемых значений МХ.

Выбирается номер , такой, что

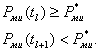
В качестве интервала между поверками берется T_l.

_{Как видно из рисунка 1 предложенный алгоритм начинается с выбора форсирующего режима. Выбор и обоснование форсирующего режима, рациональную организацию испытаний можно осуществить только после детального анализа объекта исследования и процессов его функционирования. При этом возникает необходимость принятия решений близких к оптимальным при ускоренных методах испытаний. Для решения поставленной задачи будут использованы статистические методы планирования эксперимента. Один из возможных методов приведен в [8].}

_{Для организации факторного эксперимента при ускоренных испытаниях необходимо реализовать следующие этапы}

_{1 Выбор выходного (определяющего) параметра.}

_{2 Выбор состава влияющих на выходной параметр факторов (внутренних параметров и внешних воздействий).}

_{3 Выдвижение и проверка гипотезы о виде математической модели процесса изменения выходного параметра.}

_{4 Выбор диапазонов варьирования всех факторов.}

_{5 Выбор количества опытов, т.е. определение числа узловых точек факторного пространства и числа повторений опытов в каждой точке.}

_{6 Построение матрицы планирования и проведение эксперимента.}

_{7 Вычисление коэффициентов модели.}

_{8 Оценка значимости коэффициентов модели и адекватности модели.}

_{Предложенная авторами методика позволит более достоверно определять интервалы между поверками, повысить эффективность поверочных работ и может применяться при разработке новых типов средств измерений или вводе в эксплуатацию средств измерений ввезенных по импорту в РФ.}

Литература

1 Сергеев А. Г. Метрология: Учебник. - М.: Логос, 2005. - 272 с.

2 РМГ 74-2004 ГСИ. Методы определения межповерочных и межкалибровочных интервалов средств измерений.

3 Артемьев Б.Г., Лукашов Ю.Е. Справочное пособие для работников метрологических служб – М.: Издательство стандартов, 2004. – 646 с.

4 Данилов А.А. Методы установления и корректировки межповерочных интервалов средств измерений. – Главный метролог, 2005, №6. – С. 29-37.

5 МОЗМ. МД10. Руководство по определению межповерочных интервалов средств измерений, используемых в испытательных лабораториях.

6 МИ 2554-99 Государственная система обеспечения единства измерений. Теплосчетчики. Методика испытаний с целью подтверждения межповерочных интервалов. Общие требования.

7 Дорохов А. Н., Керножицкий В. А., Миронов А. Н. Обеспечение надежности сложных технических систем: Учебник. - СПб.: Издательство «Лань», 2011. - 352 с.

8 Кострикина И.А., Мыскина Е.В. Применение методов планирования ускоренных испытаний СИ при определении межповерочных интервалов. – Мир измерений, 2012, №11. – С. 46-48.

Авторы

Кострикина Инна Анатольевна - начальник лаборатории ОАО «НИИЭМП», к.т.н.

Россия, 440000, г. Пенза. ул. Каракозова, 44

Тел. (8412) 47-72-86

Е-mail: tbmc2@mail.ru

Галкина Екатерина Николаевна - магистрант кафедры «Метрология и системы качества» Пензенского государственного университета

Россия, 440026, г. Пенза. ул. Красная, 40

Е-mail: katu000.92@mail.ru