Технические науки/5. Энергетика
УДК 621.311.004.12
К.т.н. Большанин Г.А., Большанина Л.Ю., Марьясова Е.Г.
Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
«Братский государственный университет», Россия
ИСПОЛЬЗОВАНИЕ СИСТЕМЫ «MATLAB» ДЛЯ АНАЛИЗА
ЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ
Задача электрообеспечения промышленных и
иных объектов достаточно успешно решается во всем мире. В настоящее время
известно множество способов повышения качества электрической энергии, известны
методы их реализации. Для поддержания показателей качества электрической
энергии на должном уровне необходимо проводить анализ таких характеристик электрической
энергии, как напряжение и ток [1 -5]. Для передачи электрической энергии на
дальние расстояния используют трехфазные трехпроводные линии электропередачи
напряжением свыше 35 кВ. Для расчета фазных напряжений и линейных токов
используется пакет прикладных программ Matlab [6 -7]. Законы распределения фазных напряжений и
линейных токов по однородному участку элементарной протяженности такой ЛЭП на
частоте п-й гармонической составляющей
известны [2, 3, 5] для фазы ![]() :
:
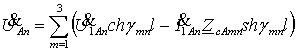 ; (1)
; (1)
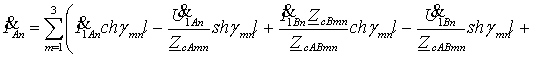
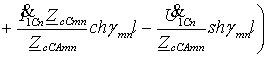 ; (2)
; (2)
где ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() – действующие значения фазных напряжений и линейных токов на частоте
п-й гармонической составляющей в
начале рассматриваемого участка ЛЭП;
– действующие значения фазных напряжений и линейных токов на частоте
п-й гармонической составляющей в
начале рассматриваемого участка ЛЭП; ![]() ,
, ![]() и
и ![]() – собственные волновые сопротивления в каждой фазе для т-й пары волн электромагнитного поля, участвующих
в передачи электрической энергии;
– собственные волновые сопротивления в каждой фазе для т-й пары волн электромагнитного поля, участвующих
в передачи электрической энергии; ![]() ,
, ![]() и
и ![]() – взаимные волновые сопротивления между линейными проводами ЛЭП
для т-й пары волн электромагнитного
поля;
– взаимные волновые сопротивления между линейными проводами ЛЭП
для т-й пары волн электромагнитного
поля; ![]() – постоянная распространения
т-й пары волн электромагнитного поля
вдоль анализируемого участка ЛЭП на частоте п-й
гармонической составляющей;
– постоянная распространения
т-й пары волн электромагнитного поля
вдоль анализируемого участка ЛЭП на частоте п-й
гармонической составляющей; ![]() – протяженность
анализируемого участка ЛЭП.
– протяженность
анализируемого участка ЛЭП.
В качестве примера могут быть использованы
спектральные составы напряжений и токов в ЛЭП-220 кВ в месте присоединения
подстанции «Лена» ОАО «Иркутскэнерго» (табл. 1). Пусть начальные фазы
напряжений и токов будут практически симметричны, то есть фазные напряжения,
также как и линейные токи отличаются друг от друга на треть периода. Причем ток
в каждом линейном проводе отстает от соответствующего напряжения на угол 200.
Таблица 1
Спектральный
состав фазных напряжений и линейных токов на ЛЭП-220 кВ (подстанция «Лена»)
|
№ гармоники |
Фазные напряжения, В |
Линейные токи, А |
||||
|
UA |
UB |
UC |
IA |
IB |
IC |
|
|
0 |
529,64 |
263,58 |
1302,5 |
2 |
2 |
0 |
|
1 |
132410 |
131790 |
130250 |
66 |
65 |
65 |
|
2 |
13,241 |
65,895 |
0 |
1 |
0,126 |
2 |
|
3 |
3310,25 |
2639,4 |
2084 |
2 |
1 |
2 |
|
4 |
13,241 |
0 |
0 |
1 |
0,063 |
1 |
|
5 |
5031,58 |
39,52,7 |
2605 |
2 |
1 |
1 |
|
6 |
13,241 |
0 |
13,025 |
1 |
0,063 |
0,0846 |
|
7 |
132,41 |
658,95 |
1432,75 |
0,1214 |
0,021 |
0,0564 |
|
8 |
13,241 |
0 |
0 |
0,0607 |
0,021 |
0,0564 |
|
9 |
662,05 |
131,79 |
13,025 |
0,0607 |
0,021 |
0,0564 |
|
10 |
13,241 |
0 |
0 |
0,0607 |
0 |
0,0282 |
|
11 |
1059,28 |
1317,9 |
1042 |
0,03035 |
0,0402 |
0,0282 |
|
12 |
13,241 |
0 |
0 |
0,0607 |
0,021 |
0,0564 |
|
13 |
3707,48 |
1317,9 |
2341,5 |
0,03035 |
0 |
0,0282 |
|
14 |
13,241 |
0 |
0 |
0,0607 |
0,021 |
0,0282 |
|
15 |
13,241 |
65,895 |
130,25 |
0,03035 |
0,042 |
0,0282 |
|
16 |
0 |
0 |
0 |
0,0607 |
0,021 |
0,0282 |
|
17 |
264,82 |
131,79 |
130,25 |
0 |
0 |
0,0282 |
Величины фазных напряжений и линейных
токов в конце участка ЛЭП протяженности l определяются по формулам подобным (1) – (2).
Для расчета фазного напряжения и построения 3D-графика в командном окне Matlab задаются диапазоны
гармоник, длины линии:
>>
n = 2:17;
>>
l = 95:105;
выравниваются
массивы:
>> [X,Y] = meshgrid (l,n);
вызывается
функция:
>>
U=Span3A (l,n).
По полученным значениям напряжения
строится график:
>>
plot3 (X,Y,abs(U)).
На рис. 1 показано распределение напряжения
в фазе ![]() вдоль анализируемого
участка ЛЭП на частотах высших гармонических (
вдоль анализируемого
участка ЛЭП на частотах высших гармонических (![]() ). Здесь видно, что в спектре фазного напряжения преобладают
величины напряжений на частотах 5-й, 7-й, 11-й и 13-й гармонических составляющих
на участках протяженностью 97 км, 98 км, 100 км, 101 км, 104 км.
). Здесь видно, что в спектре фазного напряжения преобладают
величины напряжений на частотах 5-й, 7-й, 11-й и 13-й гармонических составляющих
на участках протяженностью 97 км, 98 км, 100 км, 101 км, 104 км.
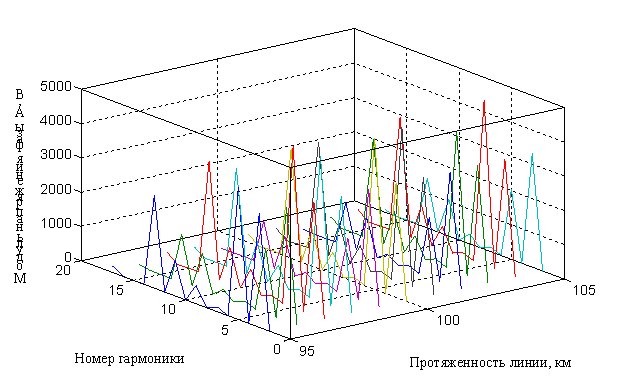
Рис. 1.
Графическая интерпретация закона распределения модуля фазного напряжения ![]() на частотах высших
гармонических составляющих
на частотах высших
гармонических составляющих
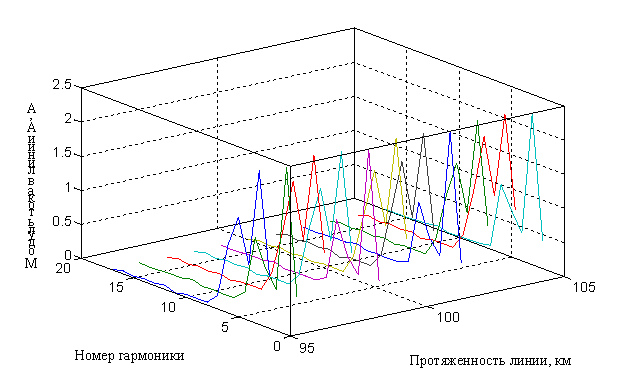
Рис. 2.
Графическая интерпретация закона распределения модуля линейного тока на частоте
высших гармонических составляющих в линии В
На рис. 2 показана графическая
интерпретация распределения линейного тока вдоль анализируемого участка ЛЭП на
частотах высших гармонических составляющих (![]() ) в линии
) в линии ![]() . Здесь видно, что наибольшие токи наблюдаются на частотах
3-й, 5-й, 7-й и 9-й гармонических составляющих. Причем величины гармонических
составляющих токов практически равновелики на протяжении всего рассматриваемого
участка линии электропередачи.
. Здесь видно, что наибольшие токи наблюдаются на частотах
3-й, 5-й, 7-й и 9-й гармонических составляющих. Причем величины гармонических
составляющих токов практически равновелики на протяжении всего рассматриваемого
участка линии электропередачи.
Литература
1.Электрическая энергия. Совместимость
технических средств электромагнитная. Нормы качества электрической энергии в
системах электроснабжения общего назначения: ГОСТ Р 54149 – 2010. – М: Стандартинформ,
2010. – 23 с.
2. Большанин Г.А. Распределение
электрической энергии пониженного качества по однородному трехпроводному участку
воздушной ЛЭП. // Научный вестник НГТУ. / Г.А. Большанин. – 2009.– №4(37).– С.
135–144.
3. Большанин Г.А. Распределение
электрической энергии пониженного качества по участкам электроэнергетических
систем. В 2-х кн. / Г.А. Большанин. – Братск: БрГУ, 2006. – 807 с.
4. Большанин Г.А. Автоматизированная
система активного контроля показателей качества электрической энергии. / Г.А.
Большанин. – Братск: БрГУ, 2006. – 152 с.
5. Большанин Г.А. Особенности
распространения электрической энергии по трехпроводной линии электропередачи. /
Г.А. Большанин, Л.Ю. Большанина, Е.Г. Марьясова. – Системы. Методы. Технологии.
– 2011. – №3(11). – С.82–89.
6. Большанин Г.А. Расчет параметров
трехфазной трехпроводной линии электропередачи (LEP3 v. 1.00):
Программа для ЭВМ. / Г.А. Большанин, Л.Ю. Большанина. – №2010611988 от
16.03.2010.
7. Большанина Л.Ю., Большанин Г.А.,
Марьясова Е.Г. Расчет параметров электрической энергии трехфазной трехпроводной
линии электропередачи в программе «LEP3»./
Л.Ю. Большанина, Г.А. Большанин, Е.Г. Марьясова. // Труды Братского
государственного университета. Серия: Естественные и инженерные науки –
развитию регионов Сибири. 2010. – Т.2. –
С. 69-73.