УДК 530.1

В.К. Федоров, Е.В. Аникина, И.Е. Пестрикова, М.Е. Пестриков, Л.Е. Пестрикова

Омский государственный технический университет, г. Омск

ГЕНЕРАТОР АНИЩЕНКО – АСТАХОВА

Еще одной моделью детерминированного хаоса является генератор Анищенко – Астахова [1, 32]. В процессе моделирования устанавливалась зависимость рассеиваемой мощности в активном нелинейном элементе (активное сопротивление) от типа колебаний в НЭЦ.

Автоколебания в системе обеспечиваются введением в контур активного сопротивления R(T), свойства которого нелинейным и инерционным образом зависят от протекающего через него тока.

Схема генератора Анищенко – Астахова изображена на рис.1. Уравнения для тока i(t) в контуре имеют вид [1]:

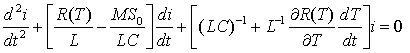
где S₀ – крутизна характеристики усилителя, который предполагается линейным, M – взаимная индуктивность цепи обратной связи, R(T) – активное сопротивление, зависящее от температуры T, L и С – индуктивность и емкость в колебательном контуре.

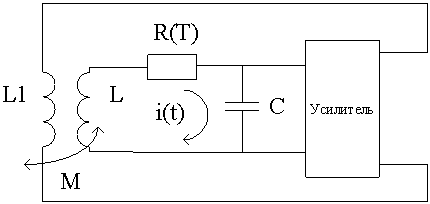
Рис. 1 Принципиальная схема генератора Анищенко – Астахова

Полагая зависимость R(T) линейной

;

и считая, что процесс теплообмена подчиняется закону Ньютона

;

где q – удельная теплоемкость нити термистора, а p – ее масса, получаем замкнутую систему вида [1]:

;

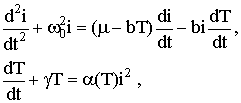где использованы обозначения:

;

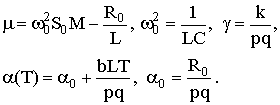В безразмерных переменных:

;

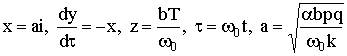уравнения принимают вид:

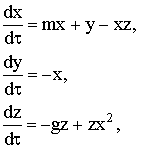
где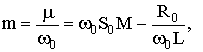

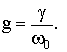
В трехмерной двухпараметрической системе уравнений параметр m пропорционален разности вносимой и рассеиваемой в контуре энергий, g – параметр, характеризующий относительное время релаксации R(T).

Библиографический список

1. Анищенко, В.С. Нелинейная динамика хаотических и стохастических систем.Фундаментальные основы и избранные проблемы / В.С. Анищенко, Т.Е. Вадивасова, В.В. Астахов; под ред. В.С.Анищенко. – Саратов: Изд-во Сарат. ун-та, 1999. – 368 с.