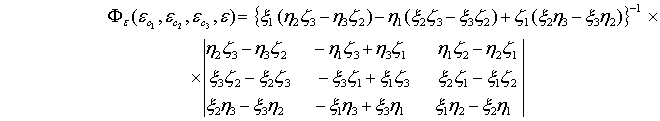Оценка эфемерид навигационных спутников на основе нелинейного фильтра Калмана

Крамаров С.О., Лукасевич В.И.

Институт управления, бизнеса и права, г. Ростов-на-Дону, Российская Федерация

Введение. Точность определения параметров движения объекта с помощью спутниковых навигационных систем (СНС) в значительной степени зависит от точности эфемеридных данных, используемых в существующих алгоритмах обработки спутниковых измерений. В свою очередь, текущее определение эфемерид осуществляется с ошибкой, зависящей от типа используемой СНС (GPS или ГЛОНАСС), степени учета возмущающих факторов, влияющих на положение спутников, частоты обновления данных и пр. и может достигать даже на небольших интервалах времени (до 30 мин.) значительных величин (десятки метров) [1,2]. При этом истинное положение спутников уточняется по радиолокационным измерениям базовых станций через заданные интервалы времени (например, в СНС ГЛОНАСС – через 30 мин.), внутри которых для вычисления навигационных параметров спутников используются детерминированные алгоритмы, не предполагающие использования каких-либо навигационных измерений и не учитывающие стохастический характер воздействий, возмущающих движение спутника [1,3]. В то же время очевидно, что их учет совместно с использованием дополнительной измерительной информации может существенно повысить точность определения эфемеридных данных [2,4-7]. В связи с этим рассмотрим возможность построения алгоритмов оценки текущих параметров реального – возмущенного, движения спутников совместно с решением навигационной задачи для любых подвижных объектов.

Постановка задачи. В связи с тем, что предлагаемый далее подход не зависит от вида используемого режима спутниковых измерений, рассмотрим далее только стандартный (автономный) режим - как наиболее универсальный, и, соответственно, только кодовые и доплеровские измерения спутниковых навигационных систем. При этом решение поставленной задачи проведем для СНС с высокой частотой поступления навигационных сообщений, позволяющей считать характер спутниковых измерений по отношению к динамике изменения навигационных параметров объекта непрерывным [6-12]. (В настоящее время частота приема спутниковых сообщений в ряде навигационных приемников (Topcon (ранее Javad), Trimble) уже составляет 100 Гц с дальнейшей тенденцией к ее увеличению [3,6,7].)

В качестве базового алгоритма вычисления спутниковых навигационных параметров далее рассмотрим алгоритм СНС ГЛОНАСС, где значения скоростей и координат _с,_с,_с спутника в гринвичской СК (ГСК) вычисляются путем решения следующей системы дифференциальных уравнений движения спутника [1]:

,

,

,

, (1)

,

,

где - угловая скорость вращения Земли,

= , =,

=,

= 398600, 44 км³/с² - гравитационная постоянная, - модуль радиуса-вектора координат _с,_с,_с спутника в гринвичской СК,

J =1082,6310^-6 – коэффициент, характеризующий несферичность нормального поля тяготения Земли (вторая зональная гармоника разложения геопотенциала в ряд по сферическим функциям),

а = 6378,136 км – большая полуось модельного эллипсоида Земли,

,,- ускорения от лунно-солнечных гравитационных возмущений, - время эфемеридных данных, с которого начинается интегрирование уравнений движения спутника (эфемеридные данные ,_с(),_с(),_с(),(),(),(),,, регистрируются приемником СНС ГЛОНАСС наравне с кодовыми и доплеровскими измерениями и обновляются 1 раз в 30 минут).

Очевидно, что при детерминированном (кусочно-постоянном) описании в (1) лунно-солнечных гравитационных возмущений не учитываются другие реальные возмущения, соизмеримые или меньшие лунно-солнечных возмущений и носящие случайный непрерывный характер, что при увеличении их интенсивности может привести к неустойчивости решения системы (1) и соответствующим «выбросам» при определении координат объекта [6,12-17]. Аппроксимируя данные множественные возмущения векторным белым гауссовским шумом (БГШ) с нулевым средним и матрицей интенсивностей , трансформируем уравнения (1) к векторной форме Ланжевена, исходной для последующего построения устойчивых алгоритмов спутниковой навигации на основе использования современных методов теории стохастической нелинейной фильтрации [4]:

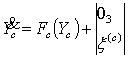, (2)

где Y = , - нулевой вектор размерности 3,

=_.

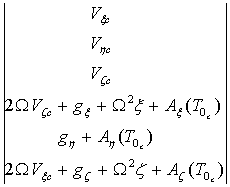Для возможности использования описания (2) при стохастической оценке параметров движения спутников необходимо, как известно, иметь уравнение наблюдателя оцениваемых параметров [4]. В качестве последнего может быть использован информационный сигнал кодовых измерений (псевдодальность), который после применения известных алгоритмов компенсации погрешностей [1] в общем случае может быть записан как [1,2]:

Z_R = +W , (3)

где _c,_c,_c – координаты спутника в ГСК, ,,- текущие координаты объекта в ГСК, W- белый гауссовский шум (БГШ) с нулевым средним и известной интенсивностью D_Z(t), обусловленный алгоритмически нескомпенсированными ошибками часов спутников и приемника, задержками сигнала при прохождении ионосферы и тропосферы, ошибками многолучевости и др. погрешностями. (Следует при этом отметить, что приведенная информационная модель наблюдения справедлива как для кодового, так и для фазового режимов измерений, поэтому полученные далее результаты носят общий характер).

Из (3) очевидна явная зависимость сигналов спутниковых измерений от текущих координат конкретного спутника, что позволяет, во-первых, осуществлять их непосредственное наблюдение на борту подвижного объекта, а во-вторых, формировать их устойчивую оценку, используя известные методы теории стохастической фильтрации.

В связи с этим в терминах теории нелинейной фильтрации задача повышения точности совместного определения эфемеридных данных и координат объекта может быть сформулирована как задача синтеза алгоритмов стохастической оценки вектора навигационных параметров спутника Y и объекта по принятым на объекте спутниковым измерениям.

Инвариантная стохастическая модель изменения навигационных параметров подвижного объекта. Но непосредственное применение теории фильтрации к системе «объект-наблюдатель» (2),(3) невозможно в силу зависимости сигнала (3) еще и от вектора координат объекта, требующего соответствующего описания, аналогичного (2). Для завершения построения модели вектора навигационных параметров, наблюдаемых в кодовых измерениях (3), проанализируем принципиальную возможность стохастического синтеза уравнений навигационных параметров любых подвижных объектов по спутниковым измерениям, обеспечивающих инвариантность алгоритмов фильтрации к виду физической модели объекта, траектории его движения, характеру возмущений и пр.

Для решения этой задачи воспользуемся моделью информационного сигнала доплеровских измерений (псевдоскорости) Z_V в автономном режиме, которая может быть представлена следующим образом [1,2]:

Z_V = []

()^-1 +, (4)

где - проекции вектора скорости спутника на оси ГСК, - проекции вектора скорости объекта на оси ГСК, W_V - БГШ с нулевым средним и известной интенсивностью D_Z(t), обусловленный нескомпенсированными погрешностями измерения.

Относительно вектора скорости объекта уравнение (4) можно переписать в виде:

[] – (Z_V - ) =

=

или в векторной форме:

, (5)

где .

Для определения всех компонентов вектора скорости объекта приведенного уравнения, полученного по доплеровским измерениям одного спутника, недостаточно. В связи с этим, для формирования недостающих уравнений предварительно введем следующие обозначения:

вектор координат i-го спутника в ГСК, V_ci= - вектор скорости i-го спутника в ГСК, Z_Vi - сигнал доплеровских измерений i-го спутника, - погрешности доплеровских измерений i-го спутника.

Для возможности полного определения вектора скорости объекта запишем систему уравнений, аналогичных (5), но построенных уже по доплеровским измерениям трех спутников [5]:

,

,

.

Обозначив далее для сокращения записи =,

, , ,

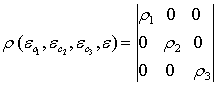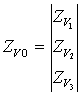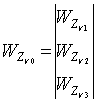запишем полученную систему уравнений в векторном виде:

.

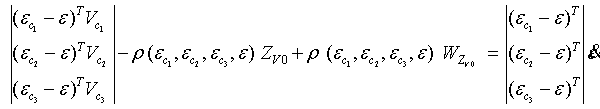Данная система легко допускает разрешение относительно вектора скорости объекта [5]:

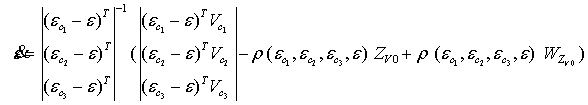,(6)

где 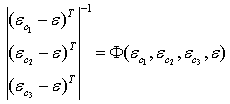- матрица, обратная матрице (приведена в Приложении).

Тогда в векторной форме Ланжевена, исходной для последующего синтеза уравнений апостериорной оценки, уравнения (6) можно представить следующим образом:

, (7)

где ,

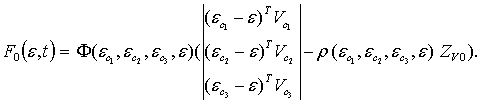
Принципиальными особенностями полученных уравнений (7) являются, во-первых, их общий характер (т.к. при их выводе не было сделано никаких упрощающих допущений о физической модели объекта, характере его движения и виде действующих на него возмущений), а во-вторых, возможность использования на их основе методов нелинейной стохастической фильтрации, обеспечивающих оптимальность оценок навигационных переменных при обработке информации с СНС.

Комплексированный вектор навигационных параметров спутников и объекта. Т.к. для формирования уравнений (7) вектора параметров движения объекта необходимо иметь точные значения навигационных параметров не одного, а трех спутников, то полный вектор оцениваемых переменных помимо вектора должен включать еще и векторы состояния этих спутников, описываемые соответствующими уравнениями, аналогичными (2):

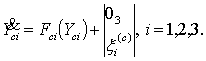
_{Полная система уравнений комплексированного вектора принимает в этом случае вид:}

,

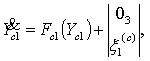
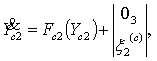
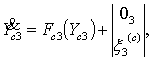
или в общей форме:

₍₈₎

_где

, , .

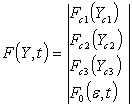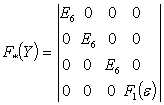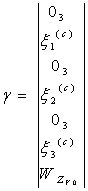Для окончательного решения задачи апостериорного оценивания комплексированного вектора Y необходимо, как и ранее, сформировать соответствующий наблюдатель его компонентов. Проведенный ранее анализ информационной модели наблюдателя (3) показывает, что сигналы кодовых измерений любого спутника явно зависят (т.е. обеспечивают полное наблюдение) как от вектора координат объекта, так и от координат этого же спутника. В связи с этим для фильтрации всего комплексированного вектора состояния Y необходимо наличие кодовых измерений со всех трех спутников. В этом случае размерность наблюдателя увеличивается до трех:

Z_R1 = +W= + W,

Z_R2 = +W= + W,

Z_R3 = +W= + W,

где Z _Ri - сигнал кодовых измерений i - го спутника,

- погрешности кодовых измерений i - го спутника,

или в векторной форме:

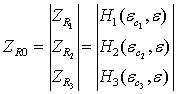
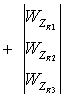= + W. (9)

Апостериорная оценка комплексированного вектора навигационных параметров. Полученное представление уравнений оцениваемых навигационных параметров в форме «объект-наблюдатель» (8), (9) позволяет построить для вектора состояния Y многомерную апостериорную плотность вероятности , знание которой в данном случае решает проблему определения любых вероятностных оценок как эфемерид спутников, так и вектора координат объекта [4]. Т.к. процедура формирования в общем случае сводится к решению многомерного интегро-дифференциального уравнения с частными производными (уравнения Стратоновича), которое в общем случае не имеет аналитического решения, то для получения оценок нелинейных процессов вида (8) используют различные приближенные (субоптимальные) методы [4], наиболее известным и востребованным из которых является обобщенный (нелинейный) фильтр Калмана. (Использование которого в системах навигации на сегодняшний день позволяет достичь необходимого компромисса между требуемой точностью и вычислительными затратами).

Исходя из уравнений «объект-наблюдатель» (8),(9) и следуя [4], обобщенный фильтр Калмана для исследуемого случая может быть записан следующим образом:

, (10)

,

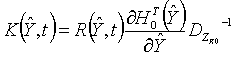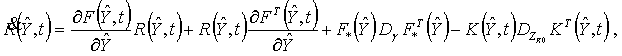
где - текущая оценка вектора , ,

- апостериорная ковариационная матрица,

_,

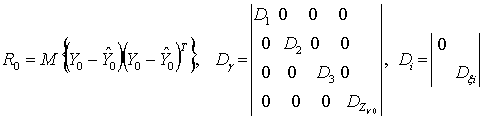матрицы интенсивностей возмущающих ускорений спутников, - матрица интенсивностей помех кодовых измерений,

- матрица интенсивностей помех доплеровских измерений.

По сравнению с традиционным подходом – вычислением эфемерид спутников в соответствии с (1) и обработкой спутниковых измерений (3),(4) с использованием итеративных алгоритмов или МНК [1], алгоритм (10) требует существенно больших вычислительных затрат (тем не менее, легко реализуемых современными вычислительными средствами в реальном времени), но за счет динамического учета и оптимальной обработки случайных возмущений эфемерид и помех спутниковых измерений позволяет обеспечить, как показано ниже, большую точность оценки навигационных параметров как спутников, так и объекта.

Интересно также отметить, что если созвездие спутников содержит спутников, то возникает возможность одновременного синтеза различных уравнений координатного вектора объекта, вектор наблюдения которого в каждом случае содержит m измерений кодовых дальностей (со всех спутников). Это, в свою очередь, приводит к возможности параллельной реализации нелинейных фильтров, аналогичных (10), - если позволяют возможности вычислителя. Одновременное формирование оценок навигационных параметров, равнозначных с информационной точки зрения, в свою очередь, позволяет существенно поднять точность позиционирования объекта и спутников за счет дополнительных процедур обработки полученных оценок – усреднения, использования метода медианы и др. робастных алгоритмов обработки статистической информации [4].

Пример. Для иллюстрации эффективности предложенного подхода было проведено моделирование алгоритма фильтрации (10) на временном интервале с шагом Dt=0,01с методом Рунге-Кутты 4-го порядка. Движение объекта задавалось по локсодромической кривой с азимутальным углом из точки с долготой - , широтой – (м) и законом изменения проекции скорости объекта на плоскость меридиана: V_М = 10 (1+sin 0.005t) м/с.

Линейное движение каждого спутника моделировалось интегрированием уравнений его движения (2) при следующих начальных условиях: для 1-го спутника - _с =, _с =, _с = , ; для 2-го - _с = 0,_с = 0,_с = , ; для 3-го - _с =, _с = 0, _с = 0, .

В качестве модели помех измерений и возмущающих ускорений спутников был использован аддитивный гауссовский вектор-шум с нулевым матожиданием и интенсивностью для: кодовых измерений – (10 м)² , доплеровских измерений - (0.25 м/с)², возмущающих ускорений - ( м/с²)².

По окончании временного интервала моделирования максимальные ошибки оценки эфемерид спутников составили: (при использовании традиционного алгоритма, соответственно: ), компонентов навигационного вектора объекта: (при использовании традиционного алгоритма - ), что свидетельствует о возможности весьма эффективного практического использования предложенного подхода.

СПИСОК ЛИТЕРАТУРЫ

1. Интерфейсный контрольный документ ГЛОНАСС (5.1 редакция). - М.: РНИИ КП, 2008 г.

2. ГЛОНАСС. Принципы построения и функционирования / Под ред. Перова А.И., Харисова В.Н. - М.: Радиотехника, 2010. - 800 с.

3. www.trimble.com

4. Тихонов В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических устройств и систем. – М.: Радио и связь, 1991. – 608 с.

5. Соколов С.В. Синтез моделей пространственных траекторий и их применение для решения задач спутниковой навигации // Прикладная физика и математика.- №2, 2013.- С.3-12.

6. Feigl, K. L, R. W. King, T. A. Herring, M. Rotchacher. A scheme for reducing the effect of selective availability on precise geodetic measurements from the Global Positioning System, Geophysical Research Letters, 18, 12891292, 1991.

7. Lichten, S.M., J.S., Border. Strategies for high-precision Global Positioning System orbit Determination, J. Geophys. Res, 92, 12751-12762, 1987.

8. Hofmann-Wellenhof, B., Lichtenegger, H., Collins, J. Some GPS Surveying Problems, Proc. of sixth Int. Geodt. sym. on Satellite Positioning ,Columbus, OHIO, pp.336-344, 1992.

9. Dow, J.M., Feltens, J., Duque, P., Sarti, F. A GPS orbit determination and analysis facility, Proc. of sixth Int. Geodt. sym. on Satellite Positioning ,Columbus, OHIO, pp.472-481, 1992.

10. Hofmann-Wellenhof B., Lichtenegger L., Collins J. Global positioning system // Theory and practice. Therrevized edition, New York, 1994.

11. Lo, Sherman C., Peterson, Benjamin B., Enge, Per K. Proving the Integrity of the Weighted Sum Squared Error (WSSE) Loran Cycle Confidence Algorithm - Navigation: The Journal of the Institute of Navigation, Vol. 54 No. 4, 2007.

12. Savage, P. G. Velocity and Position Algorithms // AIAA Journal Of Guidance, Control, And Dynamics, Vol.21, No. 2, March-April 1983, pp. 208-221.

13. Bar-Sever, Y. A new Massachusetts model for GPS yaw attitude, Journal of Geodesy, 70, 714723, 1996.

14. Schodlbauer, A., Krack, K., Scherer, B., Widmann, R. GPS Leveling in high precision engineering surveys, Proc. of sixth Int. Geodt. sym. on Satellite Positioning ,Columbus, OHIO, pp.893-903, 1992.

15. Yunck, T.P. Orbit Determination, Global Positioning System: Theory and Applications, Vol.2, Edited by Parkinson, B.W., Spilker, J.J., 1996, pp.559-592.

16. Herring, T.A. Geodetic Applications of GPS , Proceedings of The IEEE, v.87, n.1, pp.92-110, 1999.

17. Dare, P., Saleh, H. GPS Network Design: Logistics Solution Using Optimal and Near-Optimal Methods, Journal of Geodesy, vol.74, pp.467-478, 2000.

ПРИЛОЖЕНИЕ

При обозначениях:

матрица имеет вид: