Technical science /6. Electrical equipment and radio electronics

Doctor of Technical Science, professor. Basan S. N.

Russian state hydrometeorological university, branch in Tuapse, Russia

Master of Science Pivnev V. V.

Southern federal university, Russia

Conditions of reversibility of processes in linear electric chains

Now it is possible to meet various interpretation of property of reversibility. So, for example, in the theory of linear electric chains property of reversibility is formulated in the form of the theorem of reversibility (reciprocity) [1]. Its essence consists in the following. If the source of tension is in a branch with number and causes in a branch with number current , after source transfer in a branch it will cause in a branch current , such that equality will be carried out

. (1)

Other interpretation of property of reversibility is that process is considered reversible if, since some timepoint , processes in studied system take place in the return sequence [2]. In this work the vtory understanding of property of reversibility of processes is used.

Definition. Process of change of current (or tension ) in one of branches of an electric chain we will call reversible in that case when, since some timepoint , as a result of change of parameters of an equivalent circuit of an electric chain (switching), the condition is satisfied:

. (2)

Or

. (3)

At the heart of many forms of movement of a matter lie electromagnetic interactions. Therefore conditions of course of the reversible process, received bu studying of reversibility electric chains, can be extended to other forms of movement of a matter, mechanical, thermal, etc. These results can be in the long term applied to the solution of problems in various areas of practical activities (ecology, medicine, a hydromechanics, etc.). In this regard the subject of this work is greatly actual. Let's consider an equivalent circuit of any linear electric chain. Let it is required to make in this electric chain in the set timepoint switching so that current (or tension) in a branch began to change in the return sequence Generally for the set class of electric chains current changes according the law:

. (4)

Here:

- the forced component of current,

- integration constants,

- roots of the characteristic equation,

- order of an electric chain.

Applying to (3) condition (1) to the scheme after switching, we will receive:

. (5)

By simple transformations the equation (4) can be given to a look:

. (6)

In this expression: . (7)

. (8)

The demanded law of change of the forced component can achieve, having changed as appropriate parameters of independent sources of electric energy in a chain. Reversibility of process for a free component can be provided, having changed signs of the corresponding elements so that signs of roots of the characteristic equation changed on the opposite. As an example we will consider an equivalent circuit of a linear electric chain of the first order (Fig.1).

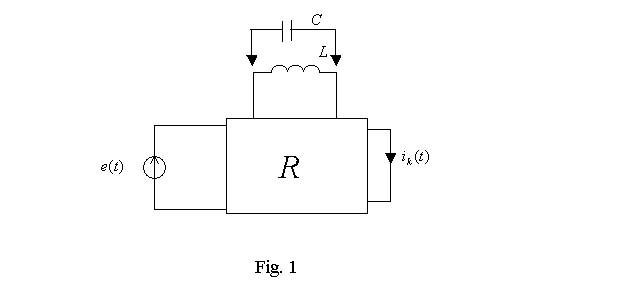
Here: - tension source,

R – linear resistive passive multiterminal network,

L – inductance,

С- capacity,

- current in k- й branches.

It is known [3] that current in randomly chosen k- й branches will change generally under the law:

. (9)

In this expression:

- the forced component of current,

A – integration constant,

- integration constant,

In order that in this equivalent circuit, since some timepoint current - started changing in the return sequence eventually, performance of the following condition is necessary:

. (10) Thus, since some timepoint current will start changing in the return sequence if in the return sequence both the forced component of current and a free component at the same time starts changing. The first condition can be satisfied by change of parameters of a source of tension, and in this work its realization isn't considered. For a free component it is possible to write down:

. (11)

The received expression differs from initial an opposite sign of a root of the characteristic equation.

(12)

Here - the entrance resistance of the resistive two-pole network from inductance provided that all sources of electric energy are excluded (are replaced with the internal resistance). The similar result turns out for an equivalent circuit of the first order with a capacity.

. (13)

Generalizing the aforesaid it is possible to draw the following conclusion:

- if in an equivalent circuit of the first order in a timepoint to change a sign of parameter of one of elements on opposite, that, from this time time, free components of currents of all elements will start changing in the return sequence.

One of arisen when performing the considered transformation of problems is realization of demanded switching. It can be rather simply solved if the switched element is an analogo-digital-to-analog element.

Literature.

1 . S. Sesha, N. Balabanyan, Analysis of linear chains, Gosenergoizdat, M, L. 1963, 551с.

2. I.V.Savelyev Kurs of physics, т.1, M, "Science", 1989, 350 pages.Л. Р.

3. Neumann, K.S.Demirchyan, Theoretical bases of electrical equipment, том1, Lenizdat, Energoizdat, 1981 of 530 pages.

4. Basan S. N., Izotov M. V. Use of microprocessor devices in problems of synthesis of nonlinear electric chains with the set properties.// Materiały VII Międzynarodowej naukowi-praktycznej konferencji «Perspektywiczne opracowania są nauką i technikami - 2011». Volume 56. Techniczne nauki.: Przemyśl. Nauka i studia, 2011. – P.17-24.

5 . Basan S. N., Izotov M. V. To a problem of a choice of analog-digital element basis at realization of nonlinear resistive two-pole networks with the set voltamperny characteristics//Izv. higher education institutions. Electromecanics. 2010 . No. 6. Page 80-83