К.т.н. Твердоступ Н.И., Еременко С.В.
Днепропетровский
национальный университет им. Олеся Гончара
ОСОБЕННОСТИ
АМПЛИТУДНО-ЧАСТОТНОЙ
ХАРАКТЕРИСТИКИ
РЕЗОНАНСНОГО ДЕЛИТЕЛЯ
НАПРЯЖЕНИЯ
Повышение чувствительности индуктивных (емкостных)
датчиков к контролируемому параметру, расширение динамического диапазона
измеряемой величины является актуальным при создании устройств измерения и контроля.
В
основу работы ряда устройств неразрушающего контроля с индуктивными
(емкостными) датчиками положен Z-метрический
метод, позволяющий определять приращение модуля комплексного сопротивления
датчика, индуктивность (емкость) которого является элементом колебательного
контура, расстроенного в пределах полосы пропускания относительно частоты
питающего контур внешнего задающего генератора
[1]. Устройства на основе Z-метра имеют невысокую чувствительность к
контролируемому параметру [2]. Попытки повысить чувствительность за счет
увеличения крутизны склона амплитудно-частотной характеристики (АЧХ) контура
неизбежно сопровождаются уменьшением динамического диапазона измерений [3].
Целью работы
является анализ АЧХ резонансного делителя напряжения для обоснования
возможности повышения чувствительности и расширения динамического диапазона
измеряемого импеданса датчика.
Схема Z-метра
(рис.1а) представляет собой частотно-зависимый делитель
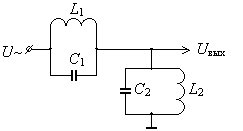
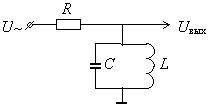
напряжения, состоящий из
активного сопротивления R и LC-контура, расстроенного в пределах полосы пропускания относительно
частоты колебаний задающего генератора. Здесь изменение выходного напряжения Uвых как функции импеданса LC-контура определяется крутизной склона его АЧХ. При
этом динамический диапазон изменения импеданса контура ограничивается шириной
АЧХ.
В схеме резонансного делителя напряжения вместо
сопротивления R включен дополнительный колебательный контур L1С1 (рис.1б)
с расстройкой, противоположной расстройке основного контура L2С2.
Для схемы резонансного делителя напряжения (рис.1б)
комплексный коэффициент передачи имеет вид
![]() (jω) = Ż2 / (Ż1 + Ż2), (1)
(jω) = Ż2 / (Ż1 + Ż2), (1)
где Ż1, Ż2
– импедансы контуров, которые
соответственно равны
Ż1 = 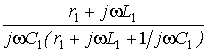 , (2)
, (2)
Ż2 =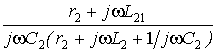 . (3)
. (3)
Обозначим
А1 = 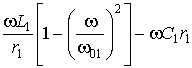 ; (4)
; (4)
А2 = 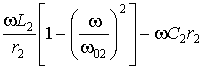 ; (5)
; (5)
В1 = 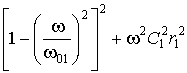 ; (6)
; (6)
В2 = 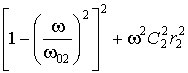 ; (7) где
; (7) где ![]() ,
, ![]() - резонансные частоты контуров, r1, r2 – активные сопротивления контуров. Найдем выражение
комплексного коэффициента передачи резонансного делителя напряжения в виде
- резонансные частоты контуров, r1, r2 – активные сопротивления контуров. Найдем выражение
комплексного коэффициента передачи резонансного делителя напряжения в виде
![]() (jω) =
(jω) = 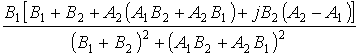 . (8)
. (8)
Амплитудно-частотная
характеристика делителя определяется модулем коэффициента передачи
׀![]() (jω)׀ =
(jω)׀ = 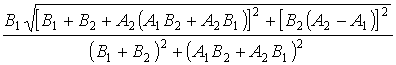 , (9)
, (9)
а фазо-частотная
характеристика
φ(ω) = arctg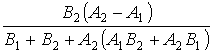 . (10)
. (10)
Для упрощения анализа
считаем, что L1 = L2 = L, r1 = r2 = r.
Качественный анализ выражения (9) показывает, что при ω02 <
ω01 зависимость ׀![]() (jω)׀ имеет вид, приведенный на рис.2. С ростом
частоты ω задающего генератора при ω = ω02 наступает резонанс токов в параллельном
контуре L2C2 нижнего
плеча делителя, при этом ׀
(jω)׀ имеет вид, приведенный на рис.2. С ростом
частоты ω задающего генератора при ω = ω02 наступает резонанс токов в параллельном
контуре L2C2 нижнего
плеча делителя, при этом ׀![]() (jω)׀ = 1.
(jω)׀ = 1.
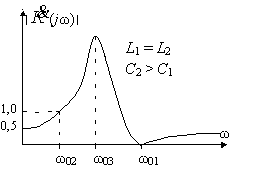
Рис.2 - Амплитудно-частотная
характеристика резонансного делителя
При дальнейшем увеличении частоты генератора ω в
диапазоне ω02 < ω < ω01 импеданс
верхнего контура L1C1 еще сохраняет индуктивный
характер, а импеданс контура L2C2 уже
становиться емкостным, следовательно, резонансный делитель можно считать
последовательным контуром с резонансной частотой ω03 = ![]() . В таком последовательном контуре при ω = ω03
наблюдается резонанс напряжений, вызывающий существенное увеличение ׀
. В таком последовательном контуре при ω = ω03
наблюдается резонанс напряжений, вызывающий существенное увеличение ׀![]() (jω)׀.
Дальнейшее увеличение ω приводит к резонансу токов в контуре L1C1 на частоте ω = ω01, при этом
׀
(jω)׀.
Дальнейшее увеличение ω приводит к резонансу токов в контуре L1C1 на частоте ω = ω01, при этом
׀![]() (jω)׀ →
0. Рабочими участками могут быть диапазоны частот ω03 <
ω < ω01 или ω02 < ω < ω03,
в которых протяженность и крутизна АЧХ определяются разностью частот ω03
и ω01 или ω03 и ω02. По
сравнению с Z-метром у резонансного делителя есть очевидное преимущество
- резонансное усиление напряжения, т.к. в рабочем диапазоне ׀
(jω)׀ →
0. Рабочими участками могут быть диапазоны частот ω03 <
ω < ω01 или ω02 < ω < ω03,
в которых протяженность и крутизна АЧХ определяются разностью частот ω03
и ω01 или ω03 и ω02. По
сравнению с Z-метром у резонансного делителя есть очевидное преимущество
- резонансное усиление напряжения, т.к. в рабочем диапазоне ׀![]() (jω)׀
преимущественно больше единицы. У Z-метра коэффициент передачи всегда меньше единицы.
(jω)׀
преимущественно больше единицы. У Z-метра коэффициент передачи всегда меньше единицы.
Выражение
(9) было протабулировано для значений L = 12 мГн, r = 10 Ом и различных соотношений между С1 и С2. На рис. 3 представлены графические зависимости
модуля коэффициента передачи ׀![]() (jω)׀.
Если датчик (индуктивный или емкостной) включить в качестве элемента нижнего
контура L2C2, то при
его расстройке за счет увеличения L2 или C2 в случае
ω02 < ω01 (рис. 3а), изменяется частота
последовательного резонанса ω03, максимум значения ׀
(jω)׀.
Если датчик (индуктивный или емкостной) включить в качестве элемента нижнего
контура L2C2, то при
его расстройке за счет увеличения L2 или C2 в случае
ω02 < ω01 (рис. 3а), изменяется частота
последовательного резонанса ω03, максимум значения ׀![]() (jω)׀, а
также крутизна склонов характеристики. Здесь исходную частоту ω внешнего
генератора следует выбирать из условия
(jω)׀, а
также крутизна склонов характеристики. Здесь исходную частоту ω внешнего
генератора следует выбирать из условия
ω02 < ω < ω03 . (11)
Тогда при уменьшении ω02 положительное
приращение ׀![]() (jω)׀
будет обусловлено двумя факторами - сдвигом характеристики влево и увеличением
максимума значения ׀
(jω)׀
будет обусловлено двумя факторами - сдвигом характеристики влево и увеличением
максимума значения ׀![]() (jω)׀. В
случае ω02 > ω01 (рис. 3б) целесообразно
условие ω03 <
ω < ω02 ,
(12)
(jω)׀. В
случае ω02 > ω01 (рис. 3б) целесообразно
условие ω03 <
ω < ω02 ,
(12)
которое обеспечивает отрицательное приращение ׀![]() (jω)׀ за
счет сдвига характеристики влево и уменьшения максимума ׀
(jω)׀ за
счет сдвига характеристики влево и уменьшения максимума ׀![]() (jω)׀.
(jω)׀.
Если
датчик включен в верхний контур L1C1 и ω02
< ω01 (рис. 3в) максимальное приращение ׀![]() (jω)׀ (с
отрицательным знаком) будет при выполнении следующего условия:
(jω)׀ (с
отрицательным знаком) будет при выполнении следующего условия:
ω03
< ω < ω01. (13)
׀к(jω)׀
ω02 >
ω01 ω02 < ω01 ׀ ׀ ω02 < ω01 ׀ ׀
![]() (jω)׀
(jω)׀
![]() (jω)׀
(jω)׀
![]() (jω)׀
(jω)׀
![]() (jω)׀
(jω)׀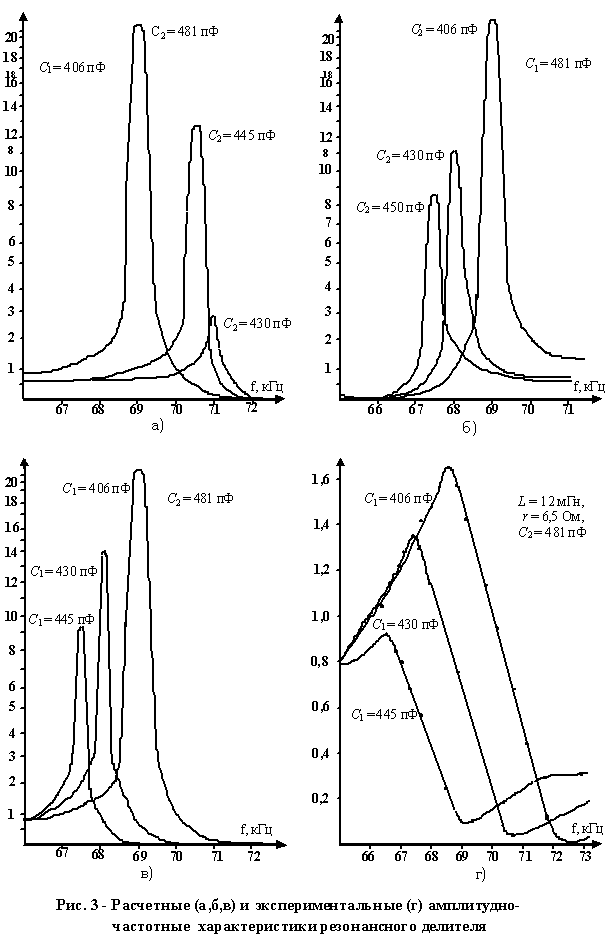
По аналогии, при выборе ω02 <
ω01 частота генератора ω должна быть
ω01 <
ω < ω03. (14)
Анализируя
условия (11), (12), (13) и (14) для резонансного делителя можно сформулировать
правила исходной настройки контуров. Если датчик включен в контур с меньшей
резонансной частотой, то частота задающего генератора должна быть большей либо
равной частоте контура с датчиком, при этом приращение ׀![]() (jω)׀
будет положительным. Если датчик включен в контур с большей резонансной
частотой, то частота задающего генератора должна быть большей либо равной
частоте последовательного резонанса, при этом приращение ׀
(jω)׀
будет положительным. Если датчик включен в контур с большей резонансной
частотой, то частота задающего генератора должна быть большей либо равной
частоте последовательного резонанса, при этом приращение ׀![]() (jω)׀
будет отрицательным. Из зависимостей на рис. 3а, 3б, 3в следует также, что
максимальная крутизна характеристики и наибольший динамический диапазон
измерений наблюдаются при частотах, находящихся между частотой последовательного
резонанса ω03 и частотой, при которой коэффициент передачи ׀
(jω)׀
будет отрицательным. Из зависимостей на рис. 3а, 3б, 3в следует также, что
максимальная крутизна характеристики и наибольший динамический диапазон
измерений наблюдаются при частотах, находящихся между частотой последовательного
резонанса ω03 и частотой, при которой коэффициент передачи ׀![]() (jω)׀ = 0.
(jω)׀ = 0.
На
рис.3г приведены экспериментальные зависимости ׀![]() (jω)׀,
которые достаточно хорошо совпадают с расчетными данными по форме и значениям
резонансных частот. Зависимости подтверждают наличие резонансного усиления, при
котором ׀
(jω)׀,
которые достаточно хорошо совпадают с расчетными данными по форме и значениям
резонансных частот. Зависимости подтверждают наличие резонансного усиления, при
котором ׀![]() (jω)׀ >1.
Уменьшение величин максимумов ׀
(jω)׀ >1.
Уменьшение величин максимумов ׀![]() (jω)׀ по
сравнению с расчетными значениями объясняется шунтирующим влиянием выходного
сопротивления задающего генератора.
(jω)׀ по
сравнению с расчетными значениями объясняется шунтирующим влиянием выходного
сопротивления задающего генератора.
Проведенный
анализ особенностей амплитудно-частотных характеристик резонансного делителя
напряжения показал возможность реализации измерителя импеданса индуктивного
(емкостного) датчика с высокой чувствительностью к контролируемому параметру
при более широком динамическом диапазоне изменения импеданса датчика, чем у
измерителей на основе Z-метра. По результатам исследований установлены
условия взаимных расстроек контуров, составляющих резонансный делитель, которые
позволяют выбрать необходимую чувствительность к контролируемому параметру и
требуемый динамический диапазон.
Литература:
1. Неразрушающий контроль металлов и изделий.
Справочник / Под ред. Г.С. Самойловича.
- М.: Машиностроение, 1976. - 456 с.
2. Приборы для
неразрушающего контроля материалов и изделий. Справочник. Кн.2 / Под ред. В.В.
Клюева. - М.: Машиностроение, 1986, - 352 с.
3. Измерения в электронике. Справочник / Под ред. В.А.
Кузнецова. - М.: Энергоатомиздат, 1987. – 512 с.