Doctor of Science Medvedev A.,
postgraduate student Maltseva T.
Siberian State Aerospace
University named after Academician M. F. Reshetnev
On a new
approach to the identification of complex processes
Introduction. It is expedient to use all
measurable variables while of multidimensional discrete-continuous processes
modeling and control but it requires a detailed analysis of not only the
process itself, but also the control tools and techniques of all the available
variables, as well as a priori information that can correspond to different
levels [3]. The omission of variables, nature and the discreteness of
measurement and control of different types of a priori information, as well as
some «liberty» in making certain assumptions that are inevitable when a mathematical
formulation of the problem can lead finally to negative consequences. All these
questions due to a large number of variables and the high complexity of the
internal connections of the studied processes (Fig. 1) are often omitted in the
modeling problems investigation from a theoretical point of view.
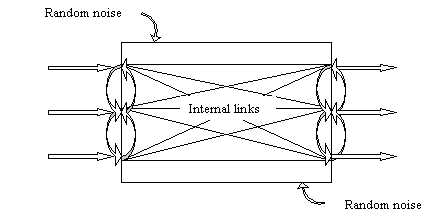
Fig. 1.
General scheme of the multidimensional multiply process
It is
simply impossible when solving the same applied problems when the investigated
process is for sure multidimensional and multiply connected. In this paper we
will present models of this type processes.
Nonparametric combined models. Often while
studying the real process we are facing the situation when information about
the form of some of its correlations is missed that leads to the greater
complexity in obtaining their parametric models. However, some correlations
technical, technological features, can be described parametrically or even can
follow the known laws of physical, chemical, electrical, mechanical and other phenomena.
Thus, different communication process can be studied in different degrees, i.e.
a priori information can belong to different levels. As a consequence, the
various mathematical problem statement from the mathematical point of view in
the framework of one of the modeling problem of the interested process.
The
objective necessity to get models of the similar processes, a lack of a priori
information, the random factors influence, with unknown characteristics,
discrepancy by sampling for measuring,
and a lack and imperfection of measuring complexes leads to assumptions and
hypotheses about the investigated process that often have little connection to
the reality. The “ignorance” about the structure must be unfortunately
replaced, saying, «Let the process be described by the equation of the
following form...» and the restriction of the control means by «Let such
factors are not changed /do not influence the process…» and so on. If our
assumptions are close enough to the reality, so we can rely on success in the
problem solving (indeed, a large number of the processes based on fundamental
laws and can be described with a high degree of accuracy), and if the
assumptions are too rough, it seems, there exist two methods. The first one is
to fill our «ignorance» about the process, when it will be possible to make an
accurate problem from a mathematical point of view. The second one is
development of the mathematical approach adequate to the level of a priori
information we have. In this paper, we will follow the second method.
Mathematical models of processes built in conditions, when a priori information
about the investigated process may simultaneously belong to several levels, and
be based on the three pillars: fundamental laws, parameterized dependencies and
connections reflecting only the dependence nature of some process variables
from others and will be called Ê-models[3].
Let’s
take an example of Ê- models building
of some technological process which complexity is represented not only in the
large dimension of the vector variables, but in the presence of backward and
cross flows in technological complex (Fig. 2). This may be the company united
in industrial complexes, and a set of different production 
stages, trade and
bank networks, and others.
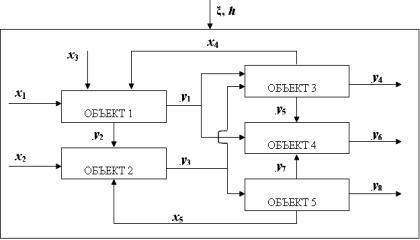xi, i = 1,…,5 – input and reduced variables;
OBJECT 3 OBJECT 1
yi,
i = 1,…,8 – input
variables;
OBJECT 5 OBJECT 4 OBJECT 2
ξ, h – random noise with zero mathematical
expectation and bounded variance influencing objects and measurement channels
Ðèñ. 2.
Conditional block diagram of the multiply connected object
As we
can see in Fig. 2, feedbacks lead to the fact that some of the vector
components of the output depends on other its components, and the investigated
class of objects is described not in the traditional form of «input - operator
- out», but in the form of equations system that determines the appropriate
implicit functions. The complex nature of internal correlations leads us to the concept of compound vectors, i.e.
vectors composed of some components of the corresponding vectors of input and
output variables [3]. For example, for an object 1 in Fig. 2 compound vectors
are 
and 
.
Let's
formulate the problem. Let for a multidimensional static object influenced by
uncontrolled disturbances with random errors having zero mathematical
expectation and limited dispersion, the following observations {X[t], Y[t]}, t=1,2,...,N of the state
vector {X, Y} may be conducted. The
probability density p(X), p(Y)
are unknown. It is known that the variables {X,
Y} on the object are connected by some relations, some of which are known
exactly (on the basis of the fundamental laws)
,others are known with accuracy to the parameter set
, and some ones due to the lack of a priori
information about the structure cannot be parameterized and presented as
high-quality ratios of input - output.
Then,
having an observation sample {X[t],
Y[t]}, t=1,2,...,N, we need to find such a value of the output
, corresponding to a given input impact -
that is, to make the forecast of the system output
according to a given input impact.
Let’s
present a model of the system in the form [3]
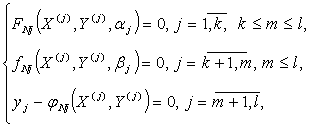(1)
where
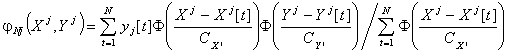(2)
- nonparametric
estimation of quality dependencies according to the observations of the state
vector of the object; 
- an equations
found on the basis of the known fundamental laws; 
- parameterized components of the corresponding vector
functions; X(j), Y(j) -vectors
composed of various components of the corresponding vectors of input and output
variables used in the description of the preferred correlations [2], Φ(.)
- bell-shaped function, parameters of fuzziness C satisfies conditions of
convergence [3].
Undoubtedly,
the offered Ê-models have a complex enough form (1), but reflect
more accurately properties of the run process in this or that object. They are
fundamentally different from the well-known models that combine equations,
obtained on the basis of the fundamental laws, technical, constructive
peculiarities of the process and its parametric and non-parametric components
as a whole.
The
model simplification of the discrete-continuous process will inevitably lead to
a deterioration of its quality, and it is possible that the simplified model,
in contrast to the models of the type (1), are not suitable for the production
of high-quality forecast systems of automatic control because of its roughness.
Note that we do not belittle the value of the classical models: they work well in
situations in which it is foreseen to their applicability. The application
of Ê-models are not available for
the of the many processes description, say, for mechanical or electrical ones, such as electrical machinery,
turbines, reactors and generators as they are controlled well enough and required
classical models. In reality, however, we have to face situations when it is
unable to receive such models for control required for the adequate
application. We want to emphasize that, in fact, a Ê-model is not uncommon and it
is not fiction, they are applied in a wide variety of natural, technological,
and social and economic processes, and that the application of the model of
such a complex form is justified. As an example we consider the process of oil
geofiltaring in a porous medium because of a spill from a pipeline.
Ê-models
the oil pollution process of the porous medium. The human activity associated
with the oil use as a primary source of energy, led to the pollution of the
environment. The most serious soil pollution by petroleum products arises from
various emergency situations. Withheld porous media hydrocarbons represent a
serious problem for the environment due to their toxicity and the potential to
serve as a long-current source of pollution. In this regard, the investigation
of the filtration processes in the models of porous media, the most adequate to
the natural conditions, is a topical issue, which will allow receiving the
forecast of forming the front of pollution and estimate the polluted zone.
The
monitoring process is of considerable complexity, because at oil pollution
interact three groups of factors to consider in assessing the effects of soil
pollution with oil and oil products: multicomponent composition of oil; the
heterogeneity of the composition and structure of soil ecosystems; the
diversity and variability of the external factors [5]. Moreover a significant
role in the formulation of modeling problems belongs to the control tools and
technology of variables control; and the investigated geofiltaring process is
unavailable to the direct investigated field (oil pollution). These
difficulties lead to the fact that at the stage of problem formulation an
investigator has to use the assumptions having little relation to reality.
Mathematical modeling is always accompanied by some assumptions that are useful
from the practical point of view in making the problem solvable. The adopted
assumptions in the general may be too «rough» and lead to the fact that the
model will be inadequate the reality. The present paper presents an attempt to
formulate the task of the modeling production process releasing some
assumptions due to the lack of a priori information. It is offered to use a new
type of mathematical models Ê-models for this purpose:
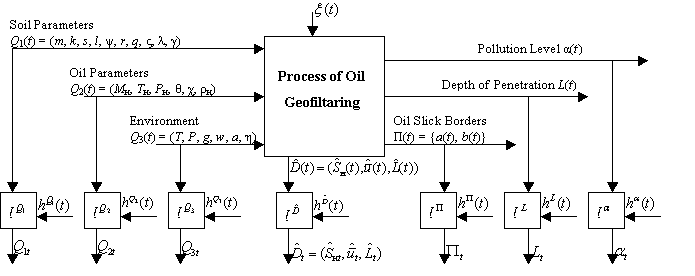
Fig. 3. Scheme of the process
geofiltaring in a porous medium
The
input variables (analogues of X in
the previously proposed problem formulation) are defined by the parameters of
three interacting systems: soil (Q1),
oil (Q2) and environment (Q3); at the output, the model
produces the spatial oil (parameters Π and L,
defining parameters of three-dimensional cylindrical surface) and the pollution
level (α) (analogues of Y).
Variables Π and L are different output variables, because they are determined by
different physical processes, and have different measurement discreetness (a
size of the spill is controlled quite often by the aerial, a depth of
penetration is measured once by carrying out prospecting ensures after the fire
season, during which the actively in the process of evaporation of light oil
fractions from the soil surface). ξ(t) – vector random effects. 
- variables of the process (saturation, filtration
rate, depth of oil pollution), determined by the model based on the equation of
continuity and Darcy’s law [5] and the
additional information about the process; H
– communication channels corresponding to different variables, which include
control measurement tools of the observed variables; Q1t, Q2t, Q3t, Dt, Ït, Lt, αt - measurement of
the corresponding variables in discrete time t; h(t) is random noise variables
measurements of the process.
We also note the significant difference of output variables Π(t), L(t)
and α(t). The output variable Π(t) is controlled by time intervals Δt, for example, on
the basis of aerial data; L(t) – through significantly large time
intervals ΔT (by drilling holes by the accepted technology),) α(t) - through T (T
> ΔT>> Δt) (with the help of chemical analysis of soil samples
by the obtained pitting [1]). The variables control α(t) for the
investigated process is often the most important from the practical point of view [1]. Despite the
fact that the process of geofiltaring is dynamic, the existing control tools were forced to consider as a
static delay, however the choice of this models class does not contradict the
modeling objectives because the simulation result has practical value at the
time when the transition process is over and passed in the established mode.
Thus,
the geofiltaring model suggested to be built on the basis of physical laws,
equations of the two-phase filtration theory [5] (fundamental dependencies),
methodologies of the main parameters calculation applied by services of
ecological safety [1], and the information about the phenomenon under
consideration obtained in earlier studies [5] (parameterized dependencies) but
also the qualitative information that can currently be presented parametrically
due to the lack of information about
the form of the relationship (non-parameterized dependencies), that leads to Ê-models.
Conclusion. The paper presents a new type
of models of a complex stochastic process, combining the equations obtained on
the basis of the fundamental laws, technical, constructive peculiarities of the
process and its parametric, and non-parametric components as a unit. The
presented models are fundamentally different from those ones used in
identification. The simulation problem formulation is carried out in conditions close to real conditions of the
similar processes, depending on the available a priori information. For
example, the process of oil geofilaring in a porous medium shows the real
necessity for the proposed models application for the complex processes
description, as proposed models make it possible to depart from a number of
assumptions on the stage of problems formulation and to get the forecasted
values of the interested process
variables in the information situation, which is really observed for such a process.
References
1. Zagvozdkin V. K., Zaikin
I. A., Bikov A. A., Makiev
U. D., Makishev D. V., Nazarov
V. B. Metodika
ocenki jekologo-jekonomicheskih posledstvij zagrjaznenija zemel' neft'ju i
nefteproduktami // Problemy analiza riska.– Moscow, 2005. – Vol. 1(2), pp.
6–28.
2. Maltseva
T. V., Medvedev A. V. O komp'juternom issledovanii K-modelej // Krasnoyarsk,
2013. – Vol. 3 (49).
3. Medvedev
A. V. Teorija neparametricheskih sistem. Modelirovanie
//Krasnoyarsk,
2010. – Vol. 4., pp. 4–9.
4.
Medvedev A. V. Computer Modeling of Active Processes // Modern Scientific
Research and Their Practical Application. – Ukraine, 2013. – Vol. J11307.
5.
Molokova N. V., Konnykh M. A. Modeling of the Dynamics of Spreading of Spilled
Hydrocarbons Taking into Account the Gravity-Capillary Interaction // Krasnoyarsk:
SFU, 2012. – Vol. 5(4), pp. 462–470.